Lungimea unui arc

În matematică , lungimea unui arc este un număr real pozitiv care măsoară intuitiv întinderea unui arc sau a unei curbe .

Deși definiția lungimii unui segment sau a unei căi poligonale a fost clară de ceva timp, o definiție generală satisfăcătoare a lungimii arcului este relativ recentă. Această problemă, numită și rectificare , a fost abordată mai întâi pentru curbe specifice și apoi rezolvată datorită calculului infinitesimal . Definiția rezultată, acceptată acum de toți matematicienii, funcționează pentru un set foarte mare de curbe, numite rectificabile .

Definiție

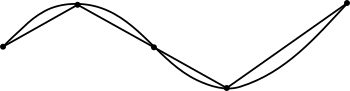
Alegând un număr finit de puncte de-a lungul curbei și conectând fiecare punct la următorul cu un segment, suma lungimilor segmentelor este lungimea „căii poligonale”. Lungimea segmentului va fi definită ca distanța dintre cele două extreme.

Lungimea curbei este cel mai mic număr pe care lungimea căii poligonale nu o poate depăși, adică este extremă superioară a lungimii căii poligonale, deoarece poligonele variază.

În termeni matematici este $\varphi :[a,b]\to X$ ${\ displaystyle \ varphi: [a, b] \ to X}$ $\ varphi: [a, b] \ la X$ curba e $(X,d)$ ${\ displaystyle (X, d)}$ $(X, d)$ un spațiu metric cu distanța d . Pentru a defini poligonul, trebuie alese punctele de pe curbă. Deci, să fie $\rho$ ${\ displaystyle \ rho}$ $\ rho$ o partiție a gamei $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$

\rho =\{t_{i}\in [a,b]:a=t_{0}<t_{1}<\ldots <t_{n}=b\}

{\ displaystyle \ rho = \ {t_ {i} \ în [a, b]: a = t_ {0} <t_ {1} <\ ldots <t_ {n} = b \}}

{\ displaystyle \ rho = \ {t_ {i} \ în [a, b]: a = t_ {0} <t_ {1} <\ ldots <t_ {n} = b \}}

Lungimea poligonului este:

d(\varphi (t_{0}),\varphi (t_{1}))+\cdots +d(\varphi (t_{n-1}),\varphi (t_{n}))=\sum _{i=1}^{n}d(\varphi (t_{i}),\varphi (t_{i-1}))

{\ displaystyle d (\ varphi (t_ {0}), \ varphi (t_ {1})) + \ cdots + d (\ varphi (t_ {n-1}), \ varphi (t_ {n})) = \ sum _ {i = 1} ^ {n} d (\ varphi (t_ {i}), \ varphi (t_ {i-1}))}

{\ displaystyle d (\ varphi (t_ {0}), \ varphi (t_ {1})) + \ cdots + d (\ varphi (t_ {n-1}), \ varphi (t_ {n})) = \ sum _ {i = 1} ^ {n} d (\ varphi (t_ {i}), \ varphi (t_ {i-1}))}

iar lungimea curbei este limita superioară a acestei cantități, deoarece partiția variază:

L(\varphi )=\sup _{\rho }\sum _{i=1}^{n}d(\varphi (t_{i}),\varphi (t_{i-1}))

{\ displaystyle L (\ varphi) = \ sup _ {\ rho} \ sum _ {i = 1} ^ {n} d (\ varphi (t_ {i}), \ varphi (t_ {i-1})) }

{\ displaystyle L (\ varphi) = \ sup _ {\ rho} \ sum _ {i = 1} ^ {n} d (\ varphi (t_ {i}), \ varphi (t_ {i-1})) }

Dacă această valoare nu este infinită, se spune că curba este rectificabilă . Curbele Peano și Koch nu sunt rectificabile. Lungimea unei curbe nu depinde de parametrizarea acesteia.

Calcul

Dacă o curbă poate fi diferențiată cu continuitate, atunci poate fi rectificată: pentru fiecare punct t al intervalului se definește o viteză și se poate arăta că lungimea definită mai sus este egală cu integrala acestei viteze pe I (când curba este în formă parametrică):

L(\varphi )=\int _{I}||\varphi ^{\prime }{(t)}||\mathrm {d} t

{\ displaystyle L (\ varphi) = \ int _ {I} || \ varphi ^ {\ prime} {(t)} || \ mathrm {d} t}

{\ displaystyle L (\ varphi) = \ int _ {I} || \ varphi ^ {\ prime} {(t)} || \ mathrm {d} t}

unde este $||\cdot ||$ ${\ displaystyle || \ cdot ||}$ ${\ displaystyle || \ cdot ||}$ este norma indusă de distanță utilizată în definiția de mai sus. Folosind noțiunea de integrală de linie putem scrie și:

L(\varphi )=\int _{\varphi }\mathrm {d} l.

{\ displaystyle L (\ varphi) = \ int _ {\ varphi} \ mathrm {d} l.}

{\ displaystyle L (\ varphi) = \ int _ {\ varphi} \ mathrm {d} l.}

Graficul unei funcții

Uneori este util să cunoașteți lungimea graficului unei funcții $f:[a,b]\to \mathbb {R}$ ${\ displaystyle f: [a, b] \ to \ mathbb {R}}$ ${\ displaystyle f: [a, b] \ to \ mathbb {R}}$ . În acest caz, graficul poate fi scris ca o curbă $\varphi :[a,b]\to \mathbb {R} ^{2}$ ${\ displaystyle \ varphi: [a, b] \ to \ mathbb {R} ^ {2}}$ ${\ displaystyle \ varphi: [a, b] \ to \ mathbb {R} ^ {2}}$ :

\left\{{\begin{matrix}x=t\\y=f(t)\end{matrix}}\right.\quad t\in [a,b]

{\ displaystyle \ left \ {{\ begin {matrix} x = t \\ y = f (t) \ end {matrix}} \ right. \ quad t \ in [a, b]}

{\ displaystyle \ left \ {{\ begin {matrix} x = t \\ y = f (t) \ end {matrix}} \ right. \ quad t \ in [a, b]}

Folosind definiția integrală a lungimii arcului ajungem la rezultat (când curba este în formă carteziană):

L(\varphi )=\int _{a}^{b}{\sqrt {1+[f'(t)]^{2}}}\,\mathrm {d} t.

{\ displaystyle L (\ varphi) = \ int _ {a} ^ {b} {\ sqrt {1+ [f '(t)] ^ {2}}} \, \ mathrm {d} t.}

{\ displaystyle L (\ varphi) = \ int _ {a} ^ {b} {\ sqrt {1+ [f '(t)] ^ {2}}} \, \ mathrm {d} t.}

Demonstrație intuitivă

Dacă împărțiți gama $[a,b]$ ${\ displaystyle [a, b]}$ $[a, b]$ în N intervale $\Delta x=(b-a)/N,$ ${\ displaystyle \ Delta x = (ba) / N,}$ ${\ displaystyle \ Delta x = (b-a) / N,}$ (cu b> a fără a pierde generalitatea), și apoi îmbinarea între $f(a+\Delta x_{i-1})$ ${\ displaystyle f (a + \ Delta x_ {i-1})}$ ${\ displaystyle f (a + \ Delta x_ {i-1})}$ Și $f(a+\Delta x_{i})$ ${\ displaystyle f (a + \ Delta x_ {i})}$ ${\ displaystyle f (a + \ Delta x_ {i})}$ , se obține cantitatea:

L_{N}=\sum _{i=1}^{N}{\ell _{i}}

{\ displaystyle L_ {N} = \ sum _ {i = 1} ^ {N} {\ ell _ {i}}}

{\ displaystyle L_ {N} = \ sum _ {i = 1} ^ {N} {\ ell _ {i}}}

unde este $\ell _{i}$ ${\ displaystyle \ ell _ {i}}$ ${\ displaystyle \ ell _ {i}}$ este lungimea îmbinării j- lea, dată ( de pitagoreic teorema ) de ${\sqrt {\left(\Delta x\right)^{2}+h^{2}}}$ ${\ displaystyle {\ sqrt {\ left (\ Delta x \ right) ^ {2} + h ^ {2}}}}$ ${\ displaystyle {\ sqrt {\ left (\ Delta x \ right) ^ {2} + h ^ {2}}}}$ , cu $h=|f(a+\Delta x_{i})-f(a+\Delta x_{i-1})|$ ${\ displaystyle h = | f (a + \ Delta x_ {i}) - f (a + \ Delta x_ {i-1}) |}$ ${\ displaystyle h = | f (a + \ Delta x_ {i}) - f (a + \ Delta x_ {i-1}) |}$ . Lungimea curbei dintre a și b este apoi dată de

L=\lim _{N\to \infty }L_{N}

{\ displaystyle L = \ lim _ {N \ to \ infty} L_ {N}}

{\ displaystyle L = \ lim _ {N \ to \ infty} L_ {N}}

.

Observând că, pentru N care are tendința la infinit, se întâmplă asta

\Delta x\to dx

{\ displaystyle \ Delta x \ to dx}

{\ displaystyle \ Delta x \ to dx}

\sum _{i}\to \int

{\ displaystyle \ sum _ {i} \ to \ int}

{\ displaystyle \ sum _ {i} \ to \ int}

h\to f^{\prime }(x)dx

{\ displaystyle h \ to f ^ {\ prime} (x) dx}

{\ displaystyle h \ to f ^ {\ prime} (x) dx}

egalitatea se reduce la

$L=\lim _{N\to \infty }\sum _{i=1}^{N}{\sqrt {\left(\Delta x\right)^{2}+h^{2}}}=\int _{a}^{b}{\sqrt {(dx)^{2}+(dx)^{2}[f^{\prime }(x)]^{2}}}=\int _{a}^{b}{{\sqrt {1+[f^{\prime }(x)]^{2}}}dx}$ ${\ displaystyle L = \ lim _ {N \ to \ infty} \ sum _ {i = 1} ^ {N} {\ sqrt {\ left (\ Delta x \ right) ^ {2} + h ^ {2} }} = \ int _ {a} ^ {b} {\ sqrt {(dx) ^ {2} + (dx) ^ {2} [f ^ {\ prime} (x)] ^ {2}}} = \ int _ {a} ^ {b} {{\ sqrt {1+ [f ^ {\ prime} (x)] ^ {2}}} dx}}$ ${\ displaystyle L = \ lim _ {N \ to \ infty} \ sum _ {i = 1} ^ {N} {\ sqrt {\ left (\ Delta x \ right) ^ {2} + h ^ {2} }} = \ int _ {a} ^ {b} {\ sqrt {(dx) ^ {2} + (dx) ^ {2} [f ^ {\ prime} (x)] ^ {2}}} = \ int _ {a} ^ {b} {{\ sqrt {1+ [f ^ {\ prime} (x)] ^ {2}}} dx}}$

QED

Dacă curba bidimensională este parametrică cu x = f (t) și y = g (t) , lungimea arcului este

s=\int _{a}^{b}{\sqrt {[f'(t)]^{2}+[g'(t)]^{2}}}\,\mathrm {d} t.

{\ displaystyle s = \ int _ {a} ^ {b} {\ sqrt {[f '(t)] ^ {2} + [g' (t)] ^ {2}}} \, \ mathrm {d } t.}

{\ displaystyle s = \ int _ {a} ^ {b} {\ sqrt {[f '(t)] ^ {2} + [g' (t)] ^ {2}}} \, \ mathrm {d } t.}

Dacă, pe de altă parte, curba este tridimensională, cu x = f (t), y = g (t), z = k (t) , lungimea arcului este

s=\int _{a}^{b}{\sqrt {[f'(t)]^{2}+[g'(t)]^{2}+[k'(t)]^{2}}}\,\mathrm {d} t.

{\ displaystyle s = \ int _ {a} ^ {b} {\ sqrt {[f '(t)] ^ {2} + [g' (t)] ^ {2} + [k '(t)] ^ {2}}} \, \ mathrm {d} t.}

{\ displaystyle s = \ int _ {a} ^ {b} {\ sqrt {[f '(t)] ^ {2} + [g' (t)] ^ {2} + [k '(t)] ^ {2}}} \, \ mathrm {d} t.}

Pentru dimensiuni superioare, procedați în același mod.

Istorie

Antichitate

În timpul istoriei matematicii , pentru o lungă perioadă de timp, chiar și cele mai bune minți au găsit imposibil să se calculeze lungimea unui arc neregulat. Deși Arhimede a inițiat aproximarea dreptunghiulară pentru a găsi zona sub o curbă cu metoda sa de epuizare , puțini credeau că este posibil ca curbele să aibă o lungime definită ca linii drepte. Așa cum se întâmplă adesea în calcule, primele rezultate au fost obținute ca aproximări. Mulți au început să înscrie poligoane cu curbe și să calculeze lungimea laturilor. Folosind din ce în ce mai multe laturi și folosind laturi mai mici, au reușit să obțină aproximări din ce în ce mai exacte.

secolul al 17-lea

În 1600 , metoda epuizării a permis rectificarea multor curbe transcendente cu metode geometrice: spirala logaritmică de Evangelista Torricelli în 1645 (unele surse spun John Wallis în anii 1650 ), cicloida de Christopher Wren în 1658 și catenaria de Gottfried Leibniz în 1691 .

Formă integrală

Înainte de dezvoltarea completă a calculului, baza pentru lungimea arcului modern sub forma unei integrale a fost descoperită independent de Hendrik van Heuraet și Pierre Fermat .

În 1659 van Heuraet a publicat o construcție care arată că lungimea unui arc poate fi interpretată ca zona sub o curbă și a aplicat-o parabolei . În 1660 , Fermat a publicat o teorie mai generală care conținea aceleași rezultate în De linearum curvarum cum lineis rectis comparatione dissertatio geometrica .

Metoda Fermat pentru determinarea lungimii unui arc

Pornind de la lucrările sale asupra tangențelor, Fermat a folosit curba

y=x^{3/2}

{\ displaystyle y = x ^ {3/2}}

{\ displaystyle y = x ^ {3/2}}

a cărei tangentă la x = a are o pantă:

{3 \over 2}a^{1/2}

{\ displaystyle {3 \ over 2} a ^ {1/2}}

{\ displaystyle {3 \ over 2} a ^ {1/2}}

de aceea linia tangentă are ecuație

y={3 \over 2}{a^{1/2}}(x-a)+f(a).

{\ displaystyle y = {3 \ peste 2} {a ^ {1/2}} (xa) + f (a).}

{\ displaystyle y = {3 \ peste 2} {a ^ {1/2}} (x-a) + f (a).}

Ulterior, a crescut a cu o cantitate mică a a + ε , făcând segmentul AC o bună aproximare pentru lungimea curbei de la A la D. Pentru a găsi lungimea segmentului AC, el a folosit teorema lui Pitagora :

{\begin{aligned}AC^{2}&{}=AB^{2}+BC^{2}\\&{}=\varepsilon ^{2}+{9 \over 4}a\varepsilon ^{2}\\&{}=\varepsilon ^{2}\left(1+{9 \over 4}a\right)\end{aligned}}

{\ displaystyle {\ begin {align} AC ^ {2} & {} = AB ^ {2} + BC ^ {2} \\ & {} = \ varepsilon ^ {2} + {9 \ over 4} a \ varepsilon ^ {2} \\ & {} = \ varepsilon ^ {2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}}

{\ displaystyle {\ begin {align} AC ^ {2} & {} = AB ^ {2} + BC ^ {2} \\ & {} = \ varepsilon ^ {2} + {9 \ over 4} a \ varepsilon ^ {2} \\ & {} = \ varepsilon ^ {2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}}

care duce la

AC=\varepsilon {\sqrt {1+{9 \over 4}a\ }}.

{\ displaystyle AC = \ varepsilon {\ sqrt {1+ {9 \ over 4} a \}}.}

{\ displaystyle AC = \ varepsilon {\ sqrt {1+ {9 \ over 4} a \}}.}

Pentru a aproxima lungimea, Fermat a adăugat într-o însumare de segmente mici. Rețineți că rezultatul modern este:

\int _{\alpha }^{\beta }{\sqrt {1+{\frac {9}{4}}x}}\,\mathrm {d} x

{\ displaystyle \ int _ {\ alpha} ^ {\ beta} {\ sqrt {1 + {\ frac {9} {4}} x}} \, \ mathrm {d} x}

{\ displaystyle \ int _ {\ alpha} ^ {\ beta} {\ sqrt {1 + {\ frac {9} {4}} x}} \, \ mathrm {d} x}

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe lungimea unui arc

linkuri externe

( EN ) Mathematics Before Calculus ( PDF ), pe math.kennesaw.edu . Adus la 10 mai 2006 (arhivat din original la 19 decembrie 2005) .
( EN ) Istoria curburii , pe brown.edu . Adus pe 2 mai 2019 (arhivat din original la 5 aprilie 2007) .
(RO) Ghid de studiu al calculului - Lungimea arcului (rectificare) , pe pinkmonkey.com.
( EN ) Indexul curbelor celebre Arhiva MacTutor History of Mathematics

Controlul autorității	GND ( DE ) 4224141-8

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică