Distribuție de către Wigner

Distribuție de către Wigner
Funcția densității probabilității
Funcția de distribuție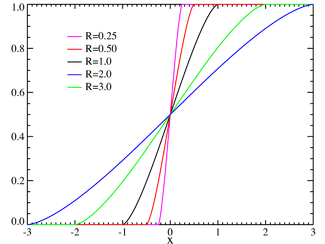
Parametrii	$r>0\$ ${\ displaystyle r> 0 \}$ $r> 0 \$ ( raza )
A sustine	$[-r,r]\$ ${\ displaystyle [-r, r] \}$ $[-r, r] \$
Funcția de densitate	${\frac {\sqrt {r^{2}-x^{2}}}{{\tfrac {1}{2}}\pi r^{2}}}$ ${\ displaystyle {\ frac {\ sqrt {r ^ {2} -x ^ {2}}} {{\ tfrac {1} {2}} \ pi r ^ {2}}}}$ ${\ frac {{\ sqrt {r ^ {2} -x ^ {2}}}} {{\ tfrac {1} {2}} \ pi r ^ {2}}}$
Funcția de distribuție	${\frac {1}{2}}+{\frac {1}{\pi r^{2}}}x{\sqrt {r^{2}-x^{2}}}+{\frac {1}{\pi }}\arcsin {\frac {x}{r}}$ ${\ displaystyle {\ frac {1} {2}} + {\ frac {1} {\ pi r ^ {2}}} x {\ sqrt {r ^ {2} -x ^ {2}}} + { \ frac {1} {\ pi}} \ arcsin {\ frac {x} {r}}}$ ${\ frac {1} {2}} + {\ frac {1} {\ pi r ^ {2}}} x {\ sqrt {r ^ {2} -x ^ {2}}} + {\ frac { 1} {\ pi}} \ arcsin {\ frac {x} {r}}$
Valorea estimata	$0\$ ${\ displaystyle 0 \}$ $0 \$
Median	$0\$ ${\ displaystyle 0 \}$ $0 \$
Modă	$0\$ ${\ displaystyle 0 \}$ $0 \$
Varianța	${\frac {r^{2}}{4}}$ ${\ displaystyle {\ frac {r ^ {2}} {4}}}$ ${\ frac {r ^ {2}} {4}}$
Indicele de asimetrie	$0\$ ${\ displaystyle 0 \}$ $0 \$
Curios	$-1\$ ${\ displaystyle -1 \}$ $-1 \$
Entropie	$\log(\pi r)-{\frac {1}{2}}$ ${\ displaystyle \ log (\ pi r) - {\ frac {1} {2}}}$ $\ log (\ pi r) - {\ frac {1} {2}}$
Funcție generatoare de momente	$2{\frac {I_{1}(rt)}{rt}}$ ${\ displaystyle 2 {\ frac {I_ {1} (rt)} {rt}}}$ $2 {\ frac {I_ {1} (rt)} {rt}}$ ( funcția Bessel de primul tip modificată )
Funcția caracteristică	$2{\frac {J_{1}(rt)}{rt}}$ ${\ displaystyle 2 {\ frac {J_ {1} (rt)} {rt}}}$ $2 {\ frac {J_ {1} (rt)} {rt}}$ ( primul tip funcție Bessel )
Manual

În teoria probabilității, distribuția Wigner (numită și semicirculară sau semi-eliptică ) este o distribuție continuă a probabilității a cărei densitate de probabilitate reprezintă o jumătate de elipsă .

Își ia numele de la fizicianul maghiar Eugene Wigner , care l-a observat prin studierea unor matrice cu coeficienți aleatori. ^[1] ^[2]

Definiție

Distribuția parametrului Wigner $r$ ${\ displaystyle r}$ $r$ are o funcție de densitate de probabilitate definită pe interval $[-r,r]$ ${\ displaystyle [-r, r]}$ $[-r, r]$ și proporțional cu funcția $y(x)={\sqrt {r^{2}-x^{2}}}$ ${\ displaystyle y (x) = {\ sqrt {r ^ {2} -x ^ {2}}}}$ $y (x) = {\ sqrt {r ^ {2} -x ^ {2}}}$ , care urmărește jumătatea „superioară” a circumferinței $x^{2}+y^{2}=r^{2}$ ${\ displaystyle x ^ {2} + y ^ {2} = r ^ {2}}$ $x ^ {2} + y ^ {2} = r ^ {2}$ . Densitatea probabilității este

f(x)={\frac {\sqrt {r^{2}-x^{2}}}{{\tfrac {1}{2}}\pi r^{2}}}

{\ displaystyle f (x) = {\ frac {\ sqrt {r ^ {2} -x ^ {2}}} {{\ tfrac {1} {2}} \ pi r ^ {2}}}}

f (x) = {\ frac {{\ sqrt {r ^ {2} -x ^ {2}}}} {{\ tfrac {1} {2}} \ pi r ^ {2}}}

,

unde factorul din numitor (corespunzător ariei semicercului) permite să fie probabilitatea totală $P([-r,r])=1$ ${\ displaystyle P ([- r, r]) = 1}$ $P ([- r, r]) = 1$ . Fiind recalificat din $y$ ${\ displaystyle y}$ $y$ , această funcție descrie jumătatea superioară a unei elipse.

În special, dacă variabila aleatorie $X$ ${\ displaystyle X}$ $X$ apoi urmează distribuția Wigner a parametrului 1 $r X$ ${\ displaystyle rX}$ $rX$ urmează parametrul distribuție Wigner $r$ ${\ displaystyle r}$ $r$ .

Caracteristici

Funcția densității probabilității distribuției Wigner este simetrică și își asumă o valoare maximă în 0. Prin urmare, speranța matematică , mediana , modul și indicele de asimetrie al distribuției sunt toate egale cu 0, la fel ca toate momentele sale de ordin impar.

Momentele sale de ordine uniformă sunt

\mu _{2k}=E[X^{2k}]={\frac {(2k)!}{k!(k+1)!}}{\frac {r^{2k}}{2^{2k}}}=({\tfrac {r}{2}})^{2k}C_{k}

{\ displaystyle \ mu _ {2k} = E [X ^ {2k}] = {\ frac {(2k)!} {k! (k + 1)!}} {\ frac {r ^ {2k}} { 2 ^ {2k}}} = ({\ tfrac {r} {2}}) ^ {2k} C_ {k}}

\ mu _ {{2k}} = E [X ^ {{2k}}] = {\ frac {(2k)!} {k! (k + 1)!}} {\ frac {r ^ {{2k} }} {2 ^ {{2k}}}} = ({\ tfrac {r} {2}}) ^ {{2k}} C_ {k}

,

unde este $C_{k}$ ${\ displaystyle C_ {k}}$ $C_ {k}$ este al k- lea număr al catalanilor . (În special pentru $r=2$ ${\ displaystyle r = 2}$ $r = 2$ momentele de ordine egală sunt numere catalane.)

În special indicele kurtozei este

\gamma _{2}={\frac {\mu _{4}}{\mu _{2}^{2}}}-3=-1

{\ displaystyle \ gamma _ {2} = {\ frac {\ mu _ {4}} {\ mu _ {2} ^ {2}}} - 3 = -1}

\ gamma _ {2} = {\ frac {\ mu _ {4}} {\ mu _ {2} ^ {2}}} - 3 = -1

.

Funcția sa generatoare de momente este

g(t)=E[e^{tX}]=2{\frac {I_{1}(rt)}{rt}}

{\ displaystyle g (t) = E [e ^ {tX}] = 2 {\ frac {I_ {1} (rt)} {rt}}}

g (t) = E [e ^ {{tX}}] = 2 {\ frac {I_ {1} (rt)} {rt}}

,

unde este $I_{1}$ ${\ displaystyle I_ {1}}$ $I_1$ este o funcție Bessel modificată de primul tip .

Funcția sa caracteristică este

\phi (t)=E[e^{itX}]=2{\frac {J_{1}(rt)}{rt}}

{\ displaystyle \ phi (t) = E [e ^ {itX}] = 2 {\ frac {J_ {1} (rt)} {rt}}}

\ phi (t) = E [e ^ {{itX}}] = 2 {\ frac {J_ {1} (rt)} {rt}}

unde este $J_{1}$ ${\ displaystyle J_ {1}}$ $J_ {1}$ este o funcție Bessel de primul fel .

Probabilitate și matrice libere

Distribuția Wigner intervine în teoria probabilității libere , pentru care variabilele aleatorii nu sunt comutative .

În special, descrie la limită numărul anumitor valori proprii ale matricilor simetrice $n\times n$ ${\ displaystyle n \ times n}$ $n \ ori n$ ai căror coeficienți sunt variabile aleatoare independente și cu aceeași distribuție de probabilitate.

În teoria probabilității „comutative”, o distribuție a probabilităților ai cărei cumulanți (indicatori „de moment ”) de ordin mai mare de doi sunt nuli este în mod necesar o distribuție normală . În același timp, în teoria probabilității libere, o distribuție ai cărei cumulanți liberi de ordin mai mare de doi sunt toți zero este în mod necesar o distribuție Wigner.

Conexiuni

Alte distribuții

Dacă variabila aleatorie $X$ ${\ displaystyle X}$ $X$ urmează parametrul distribuție Wigner $r$ ${\ displaystyle r}$ $r$ , apoi variabila aleatorie ${\tfrac {X+r}{2r}}$ ${\ displaystyle {\ tfrac {X + r} {2r}}}$ ${\ tfrac {X + r} {2r}}$ (care ia valori între 0 și 1) urmărește distribuția beta a parametrilor $({\tfrac {3}{2}},{\tfrac {3}{2}})$ ${\ displaystyle ({\ tfrac {3} {2}}, {\ tfrac {3} {2}})}$ $({\ tfrac {3} {2}}, {\ tfrac {3} {2}})$ .

Polinoame ortogonale

Polinoamele Čebyšëv de al doilea fel , definite recursiv prin $U_{0}(x)=1$ ${\ displaystyle U_ {0} (x) = 1}$ $U_ {0} (x) = 1$ , $U_{1}(x)=2x$ ${\ displaystyle U_ {1} (x) = 2x}$ $U_ {1} (x) = 2x$ Și $U_{n+1}(x)=2xU_{n}(x)-U_{n-1}(x)$ ${\ displaystyle U_ {n + 1} (x) = 2xU_ {n} (x) -U_ {n-1} (x)}$ $U _ {{n + 1}} (x) = 2xU_ {n} (x) -U _ {{n-1}} (x)$ , sunt ortogonali față de produsul interior

\langle f,g\rangle =\int _{-1}^{1}f(x)g(x){\sqrt {1-x^{2}}}dx

{\ displaystyle \ langle f, g \ rangle = \ int _ {- 1} ^ {1} f (x) g (x) {\ sqrt {1-x ^ {2}}} dx}

\ langle f, g \ rangle = \ int _ {{- 1}} ^ {1} f (x) g (x) {\ sqrt {1-x ^ {2}}} dx

.

Teoria numerelor

În teoria numerelor, distribuția Wigner este legată de conjectura Sato-Tate : dată o curbă eliptică fără multiplicare complexă $ȘI$ ${\ displaystyle E}$ $ȘI$ , numărul este luat în considerare $N_{p}$ ${\ displaystyle N_ {p}}$ $N_ {p}$ de puncte ale reducerii sale $E_{p}$ ${\ displaystyle E_ {p}}$ $E_ {p}$ într-un câmp terminat cu $p$ ${\ displaystyle p}$ $p$ elemente; acest număr este „aproximativ” $p+1$ ${\ displaystyle p + 1}$ $p + 1$ , cu o eroare care nu depășește $2{\sqrt {p}}$ ${\ displaystyle 2 {\ sqrt {p}}}$ $2 {\ sqrt {p}}$ . Conjectura Sato-Tate prezice că, pe măsură ce numerele prime variază $p$ ${\ displaystyle p}$ $p$ erori rescalate ${\tfrac {N_{p}-(p+1)}{2{\sqrt {p}}}}$ ${\ displaystyle {\ tfrac {N_ {p} - (p + 1)} {2 {\ sqrt {p}}}}}$ ${\ tfrac {N_ {p} - (p + 1)} {2 {\ sqrt {p}}}}$ sunt distribuite în funcție de distribuția Wigner a parametrului 1.

Notă

^ (EN) Wigner, E., Vectorii caracteristici ai matricilor mărginite cu dimensiuni infinite, în Ann. de matematică. , vol. 62, 1955, pp. 548-564.
^ Wigner, E., Despre distribuția rădăcinilor anumitor matrice simetrice , în Ann. de matematică. , vol. 67, 1958, pp. 325-328.

linkuri externe

(EN) Eric W. Weisstein, Legea semicercului lui Wigner în MathWorld Wolfram Research.

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] (EN) Wigner, E., Vectorii caracteristici ai matricilor mărginite cu dimensiuni infinite, în Ann. de matematică. , vol. 62, 1955, pp. 548-564.

[2] Wigner, E., Despre distribuția rădăcinilor anumitor matrice simetrice , în Ann. de matematică. , vol. 67, 1958, pp. 325-328.

[1]

[2]