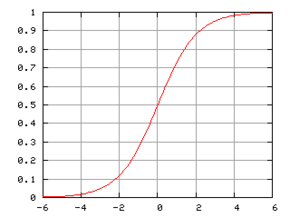
Ecuație logistică

Curba logistică (sigmoidă)

O funcție logistică sau o curbă logistică descrie o curbă S de creștere a unor tipuri de populații $P.$ ${\ displaystyle P}$ $P.$ . La început creșterea este aproape exponențială , apoi încetinește, devenind aproape liniară, pentru a ajunge la o poziție asimptotică în care nu mai există creștere (vezi graficul lateral).

Evoluția liberă a unei populații $P.$ ${\ displaystyle P}$ $P.$ poate fi modelat cu un termen de creștere $+rKP,$ ${\ displaystyle + rKP,}$ ${\ displaystyle + rKP,}$ un procent de $P.,$ ${\ displaystyle P,}$ ${\ displaystyle P,}$ dar când populația crește unii membri ai $P.$ ${\ displaystyle P}$ $P.$ , descris de termen $-rP^{2},$ ${\ displaystyle -rP ^ {2},}$ ${\ displaystyle -rP ^ {2},}$ se interferează între ei concurând pentru resurse, scăzând astfel rata de creștere, până la populație $P.$ ${\ displaystyle P}$ $P.$ încetează să crească pentru că atinge ceea ce se numește maturitate . Parametrul $K.$ ${\ displaystyle K}$ $K.$ este capacitatea portantă, factorul care limitează creșterea și care poate fi considerat blocajul .

Definiție și aplicații

O funcție logistică este definită folosind următoarea formulare:

P(t)=a{\frac {1+me^{-t/\tau }}{1+ne^{-t/\tau }}},

{\ displaystyle P (t) = a {\ frac {1 + me ^ {- t / \ tau}} {1 + ne ^ {- t / \ tau}}},}

{\ displaystyle P (t) = a {\ frac {1 + me ^ {- t / \ tau}} {1 + ne ^ {- t / \ tau}}},}

cu următorii parametri reali $la, m, n$ ${\ displaystyle a, m, n}$ ${\ displaystyle a, m, n}$ Și $\tau$ ${\ displaystyle \ tau}$ $\ tau$ . Aceste funcții găsesc aplicații într-o gamă largă de domenii, de la biologie la economie .

De exemplu, în dezvoltarea embrionului divizarea oului fertilizat începe cu o creștere exponențială: 1, 2, 4, 8, 16, 32, 64 etc. Fătul poate crește doar atât cât permite uterul; acesta și alți factori încep să încetinească creșterea numărului de celule și factorul de creștere scade chiar și pe măsură ce bebelușul continuă să crească. După momentul sarcinii , copilul se naște și începe să crească din nou. În ultima perioadă înainte de naștere, numărul de celule este aproape stabil pe o valoare asimptotică.

Un alt exemplu este concentrația de reactanți și produse în reacțiile de autocatalizare care urmează funcția logistică.

În aceste exemple se modelează relațiile dintre variabile. O funcție logistică importantă este modelul Rasch , care este un model stochastic general de măsurare. Acest model este folosit mai degrabă ca un suport pentru măsură decât pentru a modela relațiile dintre variabilele pentru care au fost făcute măsurile, ca în exemplul anterior. În special, modelul Rasch formează o bază pentru estimarea probabilității maxime a pozițiilor obiectelor care pot fi măsurate într-un spațiu continuu, pe baza culegerii de date categorice.

Ecuația lui Verhulst

Ecuația logistică, cunoscută și sub numele de model Verhulst sau curbă de creștere logistică , a fost inițial propusă ca model de creștere a populației.

Acest model presupune că:

rata de reproducere este proporțională cu populația existentă;
rata de reproducere este proporțională cu cantitatea de resurse disponibile.

Astfel, al doilea termen modelează concurența pentru resursele disponibile, care tinde să limiteze creșterea populației.

Asumand $P.$ ${\ displaystyle P}$ $P.$ reprezintă măsura populației (în ecologie se indică de obicei cu $Nu.$ ${\ displaystyle N}$ $Nu.$ ) Și $t$ ${\ displaystyle t}$ $t$ reprezintă timpul, acest model este formalizat prin ecuația diferențială :

{\frac {dP}{dt}}=rP\left(1-{\frac {P}{K}}\right)

{\ displaystyle {\ frac {dP} {dt}} = rP \ left (1 - {\ frac {P} {K}} \ right)}

{\ frac {dP} {dt}} = rP \ left (1 - {\ frac {P} {K}} \ right)

unde constanta $r$ ${\ displaystyle r}$ $r$ definește rata de creștere e $K.$ ${\ displaystyle K}$ $K.$ termenul asimptotic al populației (definit de resursele disponibile populației, cunoscut în ecologie ca capacitate de încărcare sau „capacitate de încărcare”). Termenul ${\frac {P}{K}}$ ${\ displaystyle {\ frac {P} {K}}}$ ${\ frac {P} {K}}$ reprezintă competiție intraspecifică . Soluția generală a acestor ecuații este o funcție logistică.

În ecologie , speciile sunt uneori denumite strategii r sau strategii K, în funcție de procesele selective care și-au modelat strategiile de viață.

Soluția ecuației (unde $P_{0}$ ${\ displaystyle P_ {0}}$ $P_0$ este populația inițială) este:

P(t)={\frac {KP_{0}e^{rt}}{K+P_{0}\left(e^{rt}-1\right)}},

{\ displaystyle P (t) = {\ frac {KP_ {0} e ^ {rt}} {K + P_ {0} \ left (e ^ {rt} -1 \ right)}},}

{\ displaystyle P (t) = {\ frac {KP_ {0} e ^ {rt}} {K + P_ {0} \ left (e ^ {rt} -1 \ right)}},}

adică prin colectarea și simplificarea termenului $P_{0}e^{rt}$ ${\ displaystyle P_ {0} e ^ {rt}}$ $P_ {0} și ^ {{rt}}$

P(t)={\frac {K}{1+qe^{-rt}}},

{\ displaystyle P (t) = {\ frac {K} {1 + qe ^ {- rt}}},}

{\ displaystyle P (t) = {\ frac {K} {1 + qe ^ {- rt}}},}

unde este plasat

\quad q={\frac {K-P_{0}}{P_{0}}}.

{\ displaystyle \ quad q = {\ frac {K-P_ {0}} {P_ {0}}}.}

{\ displaystyle \ quad q = {\ frac {K-P_ {0}} {P_ {0}}}.}

Din această formulare este ușor de derivat limita asimptotică:

\lim _{t\to \infty }P(t)=K.

{\ displaystyle \ lim _ {t \ to \ infty} P (t) = K.}

\ lim _ {{t \ to \ infty}} P (t) = K.

Istorie

Ecuația lui Verhulst a fost publicată pentru prima dată de Pierre F. Verhulst în 1838 , după ce a citit cartea lui Thomas Malthus „ Un eseu pe principiul populației .

Verhulst și-a derivat équation logistique ( ecuație logistică ) pentru a descrie autolimitările creșterii unei populații biologice. Ecuația este uneori numită ecuația Verhulst-Pearl după ce a fost redescoperită în 1920 . Alfred J. Lotka a dedus din nou ecuația în 1925 , numind-o legea creșterii unei populații .

Funcția sigmoidală

Același subiect în detaliu: funcția Sigmoid .

Cazul special al funcției logistice cu $a=1,m=0,n=1,\tau =1$ ${\ displaystyle a = 1, m = 0, n = 1, \ tau = 1}$ ${\ displaystyle a = 1, m = 0, n = 1, \ tau = 1}$ , acesta este

P(t)={\frac {1}{1+e^{-t}}}

{\ displaystyle P (t) = {\ frac {1} {1 + e ^ {- t}}}}

P (t) = {\ frac {1} {1 + e ^ {{- t}}}}

se numește funcție sigmoidă sau curbă sigmoidă . Numele se datorează formei grafului său analog cu a $S.$ ${\ displaystyle S}$ $S.$ . Această funcție mai este numită „funcția logistică standard” și este întâlnită adesea în multe domenii tehnice, în special în rețelele neuronale ca funcție de transfer , în probabilitate , statistici , biomatematică , psihologie matematică și în economie .

Caracterizarea matematică: studiul funcției

Sigmoid și derivate (primul derivat în roșu, al doilea derivat în negru)

Având în vedere ecuația logistică / sigmoidală într-o formă mai generală:

y(x)={a \over 1+b\cdot e^{-c\cdot x}}+d,

{\ displaystyle y (x) = {a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d,}

{\ displaystyle y (x) = {a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d,}

cu:

$e\approx 2,718$ ${\ displaystyle are \ approx 2.718}$ $și \ aproximativ 2.718$ numărul de Napier ;
$a,b,c,d>0$ ${\ displaystyle a, b, c, d> 0}$ $a, b, c, d> 0$ coeficienții ecuației.

Domeniu (câmp de definiție)
$\forall x\in \mathbb {R} .$ ${\ displaystyle \ forall x \ in \ mathbb {R}.}$ ${\ displaystyle \ forall x \ in \ mathbb {R}.}$
Studiul asimptotelor
1. Asimptotă orizontală superioară:
  $\lim _{x\to +\infty }\left({a \over 1+b\cdot e^{-c\cdot x}}+d\right)=a+d.$ ${\ displaystyle \ lim _ {x \ to + \ infty} \ left ({a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d \ right) = a + d.}$ ${\ displaystyle \ lim _ {x \ to + \ infty} \ left ({a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d \ right) = a + d.}$
2. Asimptotă orizontală inferioară:
  $\lim _{x\to -\infty }\left({a \over 1+b\cdot e^{-c\cdot x}}+d\right)=d.$ ${\ displaystyle \ lim _ {x \ to - \ infty} \ left ({a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d \ right) = d.}$ ${\ displaystyle \ lim _ {x \ to - \ infty} \ left ({a \ over 1 + b \ cdot e ^ {- c \ cdot x}} + d \ right) = d.}$
Primul derivat
${d \over dx}y(x)={abce^{cx} \over (b+e^{cx})^{2}}.$ ${\ displaystyle {d \ over dx} y (x) = {abce ^ {cx} \ over (b + e ^ {cx}) ^ {2}}.}$ ${\ displaystyle {d \ over dx} y (x) = {abce ^ {cx} \ over (b + e ^ {cx}) ^ {2}}.}$
1. Limitele primei derivate:
  $\lim _{x\to \infty }{abce^{cx} \over (b+e^{cx})^{2}}=0.$ ${\ displaystyle \ lim _ {x \ to \ infty} {abce ^ {cx} \ over (b + e ^ {cx}) ^ {2}} = 0.}$ ${\ displaystyle \ lim _ {x \ to \ infty} {abce ^ {cx} \ over (b + e ^ {cx}) ^ {2}} = 0.}$
2. Semnul primei derivate:
  ${d \over dx}y(x)>0,\quad \forall x\in \mathbb {R} .$ ${\ displaystyle {d \ over dx} y (x)> 0, \ quad \ forall x \ in \ mathbb {R}.}$ ${\ displaystyle {d \ over dx} y (x)> 0, \ quad \ forall x \ in \ mathbb {R}.}$
A doua derivată
${d^{2} \over dx^{2}}y(x)={abc^{2}e^{cx}(b-e^{cx}) \over (b+e^{cx})^{3}}.$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x) = {abc ^ {2} e ^ {cx} (be ^ {cx}) \ over (b + e ^ {cx} ) ^ {3}}.}$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x) = {abc ^ {2} e ^ {cx} (be ^ {cx}) \ over (b + e ^ {cx} ) ^ {3}}.}$
1. Limitele celei de-a doua derivate:
  $\lim _{x\to \infty }{abc^{2}e^{cx}(b-e^{cx}) \over (b+e^{cx})^{3}}=0.$ ${\ displaystyle \ lim _ {x \ to \ infty} {abc ^ {2} e ^ {cx} (be ^ {cx}) \ over (b + e ^ {cx}) ^ {3}} = 0. }$ ${\ displaystyle \ lim _ {x \ to \ infty} {abc ^ {2} e ^ {cx} (be ^ {cx}) \ over (b + e ^ {cx}) ^ {3}} = 0. }$
2. Concavitatea funcției:
  ${d^{2} \over dx^{2}}y(x)>0,\quad \forall x\in \left(-\infty ,{\lg b \over c}\right)$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x)> 0, \ quad \ forall x \ in \ left (- \ infty, {\ lg b \ over c} \ right)}$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x)> 0, \ quad \ forall x \ in \ left (- \ infty, {\ lg b \ over c} \ right)}$
  ${d^{2} \over dx^{2}}y(x)<0,\quad \forall x\in \left({\lg b \over c},\infty \right).$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x) <0, \ quad \ forall x \ in \ left ({\ lg b \ over c}, \ infty \ right).}$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x) <0, \ quad \ forall x \ in \ left ({\ lg b \ over c}, \ infty \ right).}$
3. Punct de inflexiune :
  ${d^{2} \over dx^{2}}y(x)=0\Rightarrow x_{F}={\lg b \over c}$ ${\ displaystyle {d ^ {2} \ over dx ^ {2}} y (x) = 0 \ Rightarrow x_ {F} = {\ lg b \ over c}}$ ${d ^ {2} \ over dx ^ {2}} y (x) = 0 \ Rightarrow x_ {F} = {\ lg b \ over c}$
  ${d \over dx}y(x_{F})=0\Rightarrow {d \over dx}y\left({\lg b \over c}\right)={ac \over 4}$ ${\ displaystyle {d \ over dx} y (x_ {F}) = 0 \ Rightarrow {d \ over dx} y \ left ({\ lg b \ over c} \ right) = {ac \ over 4}}$ ${\ displaystyle {d \ over dx} y (x_ {F}) = 0 \ Rightarrow {d \ over dx} y \ left ({\ lg b \ over c} \ right) = {ac \ over 4}}$
  $y_{x_{F}}={ac \over 4}\cdot x+{2(a+2d)-a\lg b \over 4}$ ${\ displaystyle y_ {x_ {F}} = {ac \ over 4} \ cdot x + {2 (a + 2d) -a \ lg b \ over 4}}$ $y _ {{x_ {F}}} = {ac \ over 4} \ cdot x + {2 (a + 2d) -a \ lg b \ over 4}$
  $P(x_{F},y_{F})=\left({\lg b \over c},{a+2d \over 2}\right).$ ${\ displaystyle P (x_ {F}, y_ {F}) = \ left ({\ lg b \ over c}, {a + 2d \ over 2} \ right).}$ ${\ displaystyle P (x_ {F}, y_ {F}) = \ left ({\ lg b \ over c}, {a + 2d \ over 2} \ right).}$
Primitiv
$\int y(x)\,\mathrm {d} x={a\lg(e^{cx}+b)+cdx \over c}+{\text{costante}}.$ ${\ displaystyle \ int y (x) \, \ mathrm {d} x = {a \ lg (e ^ {cx} + b) + cdx \ over c} + {\ text {constant}}.}$ ${\ displaystyle \ int y (x) \, \ mathrm {d} x = {a \ lg (e ^ {cx} + b) + cdx \ over c} + {\ text {constant}}.}$

Proprietățile funcției sigmoide

Funcția sigmoidă (standard) este soluția ecuației diferențiale neliniare de primul ordin

{\frac {dP}{dt}}=P(1-P),

{\ displaystyle {\ frac {dP} {dt}} = P (1-P),}

{\ displaystyle {\ frac {dP} {dt}} = P (1-P),}

cu condiții de graniță $P(0)=1/2$ ${\ displaystyle P (0) = 1/2}$ $P (0) = 1/2$ . Ecuația (2) este versiunea continuă a hărții logistice .

Curba sigmoidă arată mai întâi o creștere exponențială pentru $t$ ${\ displaystyle t}$ $t$ negativ, care încetinește până la o creștere liniară de 1/4 panta în jur $t=0,$ ${\ displaystyle t = 0,}$ ${\ displaystyle t = 0,}$ apoi se apropie $y=1$ ${\ displaystyle y = 1}$ $y = 1$ (asimptotă orizontală) cu o descompunere exponențială.

Funcția logistică este inversa funcției logit naturale și poate fi astfel utilizată pentru a converti jurnalul probabilității într-o probabilitate; conversia din raportul log-probabilitate a două alternative conduce, de asemenea, la forma unei curbe sigmoidale.

Model de creștere

Comparație între curba logistică și curba de creștere exponențială (Malthusian). Parametrii sunt:

k=10,N_{0}=1,r=1

{\ displaystyle k = 10, N_ {0} = 1, r = 1}

k = 10, N_ {0} = 1, r = 1

Comparație între curba de creștere exponențială și sigmoidală.

K=2000,N_{0}=10,r=2

{\ displaystyle K = 2000, N_ {0} = 10, r = 2}

K = 2000, N_ {0} = 10, r = 2

După ce am presupus că numărul de indivizi dintr-o populație este o funcție continuă a timpului $N(t)$ ${\ displaystyle N (t)}$ ${\ displaystyle N (t)}$ care admite o derivată continuă, avem că creșterea populației pe măsură ce timpul variază poate fi reprezentată de derivata lui $N(t)$ ${\ displaystyle N (t)}$ ${\ displaystyle N (t)}$ , care într-un model elementar poate fi presupus a fi direct proporțional cu numărul de indivizi din populația însăși.

Prin urmare, avem următoarea ecuație diferențială:

{d \over dt}N=rN(t),

{\ displaystyle {d \ over dt} N = rN (t),}

{\ displaystyle {d \ over dt} N = rN (t),}

cu $r$ ${\ displaystyle r}$ $r$ : Parametru de creștere malthusian (rata maximă de creștere a populației).

Prin urmare dacă $r$ ${\ displaystyle r}$ $r$ este o constantă a populației crește exponențial cu o pantă dependentă de $r$ ${\ displaystyle r}$ $r$ .

Pe de altă parte, într-un mediu în care disponibilitatea resurselor este limitată, evoluția populației poate fi descrisă utilizând un coeficient $r$ ${\ displaystyle r}$ $r$ care scade pe măsură ce crește populația: cel mai simplu model este $r(t):=a-bN(t)$ ${\ displaystyle r (t): = a-bN (t)}$ $r (t): = a-bN (t)$ cu $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ constant. Înlocuind această funcție în ecuația diferențială anterioară obținem:

{\frac {dN}{dt}}=aN(t)-bN^{2}(t)

{\ displaystyle {\ frac {dN} {dt}} = aN (t) -bN ^ {2} (t)}

{\ frac {dN} {dt}} = aN (t) -bN ^ {2} (t)

care poate fi pus sub forma:

{\frac {dN}{dt}}=aN\left(1-{\frac {N}{K}}\right)

{\ displaystyle {\ frac {dN} {dt}} = aN \ left (1 - {\ frac {N} {K}} \ right)}

{\ frac {dN} {dt}} = aN \ left (1 - {\ frac {N} {K}} \ right)

cu $K={\frac {a}{b}}$ ${\ displaystyle K = {\ frac {a} {b}}}$ $K = {\ frac {a} {b}}$ care este așa-numita populație maximă durabilă e $la$ ${\ displaystyle a}$ $la$ egal cu parametrul de creștere Malthusian. Aceasta este ecuația logistică a lui Verhulst.

Prin separarea variabilelor obținem:

{\frac {1}{a}}\int \left({\frac {1}{N}}+{\frac {b}{a-bN}}\right)dN(t)=\int dt.

{\ displaystyle {\ frac {1} {a}} \ int \ left ({\ frac {1} {N}} + {\ frac {b} {a-bN}} \ right) dN (t) = \ int dt.}

{\ displaystyle {\ frac {1} {a}} \ int \ left ({\ frac {1} {N}} + {\ frac {b} {a-bN}} \ right) dN (t) = \ int dt.}

Soluție de ecuație diferențială

Rezolvarea integralelor, alegerea ca primitive a celor care $N(t_{0})=N_{0}$ ${\ displaystyle N (t_ {0}) = N_ {0}}$ $N (t_ {0}) = N_ {0}$ și folosind proprietățile logaritmilor obținem soluția:

N(t)={\frac {k}{1+({\frac {k}{N_{0}}}-1)e^{-a(t-t_{0})}}}.

{\ displaystyle N (t) = {\ frac {k} {1 + ({\ frac {k} {N_ {0}}} - 1) e ^ {- a (t-t_ {0})}}} .}

{\ displaystyle N (t) = {\ frac {k} {1 + ({\ frac {k} {N_ {0}}} - 1) e ^ {- a (t-t_ {0})}}} .}

Se remarcă faptul că, din cauza supraaglomerării populației nu mai crește exponențial, ci converge la valoarea asimptotică $k$ ${\ displaystyle k}$ $k$ indiferent de $N_{0}$ ${\ displaystyle N_ {0}}$ $N_ {0}$ .

Soluția ecuației poate fi scrisă și în următoarele forme:

N(t)={kN_{0}e^{rt} \over k-N_{0}\cdot (1-e^{rt})}={kN_{0} \over N_{0}+(k-N_{0})\cdot e^{-rt}}.

{\ displaystyle N (t) = {kN_ {0} e ^ {rt} \ over k-N_ {0} \ cdot (1-e ^ {rt})} = {kN_ {0} \ over N_ {0} + (k-N_ {0}) \ cdot e ^ {- rt}}.}

{\ displaystyle N (t) = {kN_ {0} e ^ {rt} \ over k-N_ {0} \ cdot (1-e ^ {rt})} = {kN_ {0} \ over N_ {0} + (k-N_ {0}) \ cdot e ^ {- rt}}.}

Este imediat să verificăm dacă această soluție are două asimptote orizontale:

\lim _{n\to \infty }{N(t)}=K;

{\ displaystyle \ lim _ {n \ to \ infty} {N (t)} = K;}

{\ displaystyle \ lim _ {n \ to \ infty} {N (t)} = K;}

\lim _{n\to -\infty }{N(t)}=0.

{\ displaystyle \ lim _ {n \ to - \ infty} {N (t)} = 0.}

{\ displaystyle \ lim _ {n \ to - \ infty} {N (t)} = 0.}

Există un comportament diferit în caz $N_{0}>k$ ${\ displaystyle N_ {0}> k}$ ${\ displaystyle N_ {0}> k}$ atunci a doua limită ar tinde să $-\infty$ ${\ displaystyle - \ infty}$ $- \ infty$ , prezentând, de asemenea, o asimptotă verticală, dar aceste soluții nu sunt luate în considerare în modelul de creștere (ele descriu evident o populație în scădere rapidă ca fiind inițial mai mare decât resursele prezente).

Modele mai complexe

Dacă populația închisă este supusă unor dezastre periodice, adică se face retragerea $p$ ${\ displaystyle p}$ $p$ constantă în timp (imaginați-vă un lac cu pește din care se pescuiște o cotă fixă zilnică) ecuația Verhulst devine:

{\frac {d}{dt}}N=aN(t)-bN^{2}(t)-p.

{\ displaystyle {\ frac {d} {dt}} N = aN (t) -bN ^ {2} (t) -p.}

{\ displaystyle {\ frac {d} {dt}} N = aN (t) -bN ^ {2} (t) -p.}

Această ecuație este dificil de rezolvat, dar este posibil să o analizăm calitativ considerând că derivata lui $N(t)$ ${\ displaystyle N (t)}$ ${\ displaystyle N (t)}$ se anulează în:

s_{1}={\frac {a}{2b}}+{\sqrt {{\frac {a^{2}}{4b^{2}}}-{\frac {p}{b}}}}

{\ displaystyle s_ {1} = {\ frac {a} {2b}} + {\ sqrt {{\ frac {a ^ {2}} {4b ^ {2}}} - {\ frac {p} {b }}}}}

s_ {1} = {\ frac {a} {2b}} + {\ sqrt {{\ frac {a ^ {2}} {4b ^ {2}}} - {\ frac {p} {b}}} }

Și

s_{2}={\frac {a}{2b}}-{\sqrt {{\frac {a^{2}}{4b^{2}}}-{\frac {p}{b}}}}

{\ displaystyle s_ {2} = {\ frac {a} {2b}} - {\ sqrt {{\ frac {a ^ {2}} {4b ^ {2}}} - {\ frac {p} {b }}}}}

s_ {2} = {\ frac {a} {2b}} - {\ sqrt {{\ frac {a ^ {{2}}} {4b ^ {{2}}}} - {\ frac {p} { b}}}}

cu

a^{2}-4bp\geq 0

{\ displaystyle a ^ {2} -4bp \ geq 0}

a ^ {2} -4bp \ geq 0

de la care

p\leq {\frac {a^{2}}{4b}}.

{\ displaystyle p \ leq {\ frac {a ^ {2}} {4b}}.}

{\ displaystyle p \ leq {\ frac {a ^ {2}} {4b}}.}

Loc $N^{'}(t)=Y(N(t))$ ${\ displaystyle N ^ {'} (t) = Y (N (t))}$ $N ^ {{'}} (t) = Y (N (t))$ Și $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ ansamblul de funcții $N(t)$ ${\ displaystyle N (t)}$ ${\ displaystyle N (t)}$ dupa cum $N_{0}$ ${\ displaystyle N_ {0}}$ $N_ {0}$ care satisface ecuația Verlhust cu retragere constantă avem că:

În interval $s_{2}<N(t)<s_{1},$ ${\ displaystyle s_ {2} <N (t) <s_ {1},}$ ${\ displaystyle s_ {2} <N (t) <s_ {1},}$ Acolo $Da$ ${\ displaystyle Y}$ $Da$ deci funcțiile de $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ în plus, ele cresc monoton $Y(s_{1})=0$ ${\ displaystyle Y (s_ {1}) = 0}$ $Y (s_ {1}) = 0$ deci converg asimptotic la $s_{1}$ ${\ displaystyle s_ {1}}$ $s_ {1}$ .
În interval $N(t)>s_{1},$ ${\ displaystyle N (t)> s_ {1},}$ ${\ displaystyle N (t)> s_ {1},}$ Acolo $Da$ ${\ displaystyle Y}$ $Da$ deci funcțiile de $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ sunt, de asemenea, monotone în scădere $Y(s_{1})=0$ ${\ displaystyle Y (s_ {1}) = 0}$ $Y (s_ {1}) = 0$ deci converg asimptotic la $s_{1}$ ${\ displaystyle s_ {1}}$ $s_ {1}$ .
În interval $0<N(t)<s_{2},$ ${\ displaystyle 0 <N (t) <s_ {2},}$ ${\ displaystyle 0 <N (t) <s_ {2},}$ Acolo $Da$ ${\ displaystyle Y}$ $Da$ deci funcțiile de $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ sunt monotone în scădere, deci se sting după un anumit timp $t*$ ${\ displaystyle t *}$ $t *$ (nu uitați că valorile populației trebuie să fie mai mari decât zero).
Pentru $N(t)=s_{1}$ ${\ displaystyle N (t) = s_ {1}}$ $N (t) = s_ {1}$ sau $N(t)=s_{2}$ ${\ displaystyle N (t) = s_ {2}}$ $N (t) = s_ {2}$ , da $Y=0$ ${\ displaystyle Y = 0}$ ${\ displaystyle Y = 0}$ , de aici și funcțiile $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ ramane constant.

Prin urmare, în caz de retragere nu numai că trebuie să fie $p\leq {\frac {a^{2}}{4b}}$ ${\ displaystyle p \ leq {\ frac {a ^ {2}} {4b}}}$ $p \ leq {\ frac {a ^ {2}} {4b}}$ dar populația inițială nu trebuie să fie mai mică de $s_{2}$ ${\ displaystyle s_ {2}}$ $s_ {2}$ după cum se poate vedea din (3). De asemenea, se remarcă faptul că $s_{1}<k$ ${\ displaystyle s_ {1} <k}$ $s_ {1} <k$ , adică în cazul retragerii în ipoteza (1) și (2), populația converge în mod evident la o valoare mai mică decât în cazul în care nu există retragere.

Pentru a descrie mai bine cazul în care populația poate dispărea, ecuația poate fi modificată:

{d \over dt}N=rN\left(1-{N \over K}\right)\left(1-{m \over P}\right),

{\ displaystyle {d \ over dt} N = rN \ left (1- {N \ over K} \ right) \ left (1- {m \ over P} \ right),}

{\ displaystyle {d \ over dt} N = rN \ left (1- {N \ over K} \ right) \ left (1- {m \ over P} \ right),}

unde este $m$ ${\ displaystyle m}$ $m$ reprezintă nivelul minim al populației sub care acesta dispare (gândindu-se întotdeauna la lacul speciilor, adulții sunt incapabili să se împerecheze).

Un alt pas este introducerea unei anumite întârzieri în atingerea asimptotei orizontale (faza de maturitate); această nouă situație este descrisă de următoarea ecuație:

{d \over dt}N=rN(t)\left(1-{N(t-t_{m}) \over k}\right),

{\ displaystyle {d \ over dt} N = rN (t) \ left (1- {N (t-t_ {m}) \ over k} \ right),}

{\ displaystyle {d \ over dt} N = rN (t) \ left (1- {N (t-t_ {m}) \ over k} \ right),}

cu această ecuație introducem o oscilație, ca un sistem de amortizor cu arc , care oscilează în jurul poziției de echilibru într-un mod decremental, dar infinit.

În economie: difuzarea inovațiilor

Funcția logistică poate fi utilizată pentru a ilustra progresul difuzării unei inovații tehnice , de-a lungul ciclului său de viață . Din punct de vedere istoric, când sunt introduse produse noi, se investesc multe în cercetare și dezvoltare ; acest lucru duce la îmbunătățiri semnificative ale calității și reduce costurile . Toate acestea implică o perioadă de creștere rapidă a industriei. Iată câteva bunuri și servicii implicate în acest fenomen: căi ferate , lămpi cu incandescență , electrificare , Ford Model T , aviație și calculatoare . În cele din urmă, creșterile drastice ale eficienței , precum și oportunitățile asociate de reducere a costurilor sunt epuizate; în același timp, produsul sau procesul în cauză se răspândește saturând piața , lăsând puțini potențiali noi cumpărători .

Funcția logistică a fost utilizată în articole de mai mulți cercetători ai IIASA ( Institutul Internațional de Analiză a Sistemelor Aplicate ). În aceste publicații sunt studiate teme precum: diseminarea diferitelor inovații și infrastructuri ; înlocuirea surselor de energie ; rolul muncii fizice în economie sau în ciclurile de producție pe termen lung. Robert Ayres ( 1989 ) ^[1] și Cesare Marchetti ( 1988 , 1996 ) ^[2] ^{[3] au} tratat așa-numitele valuri Kondratiev , ciclurile de producție macroeconomice sinusoidale și difuzarea inovațiilor. O carte a lui Arnulf Grübler ( 1990 ) oferă o prezentare detaliată a difuzării infrastructurilor, inclusiv canale , căi ferate, autostrăzi și linii aeriene , demonstrând că este bine reprezentată de o curbă logistică adecvată ^[4] .

Carlota Perez ( 2002 ) ^{[5] a} ales curba logistică pentru a explica și dezvolta undele K menționate anterior, introducând câțiva termeni cheie: irupție , pentru începutul unei ere tehnologice ; frenezie , pentru a indica răspândirea inițială; sinergie , adică dezvoltarea sa rapidă; maturitate , pentru a indica difuziunea sa completă.

Critici

În ciuda popularității sale persistente ca model pentru creșterea populației în domeniul dinamicii populației , această utilizare a funcției logistice a fost puternic criticată. Demograful și profesorul Joel E. Cohen ( How Many People Can The Earth Support , 1995), unul dintre critici, explică faptul că Verhulst a încercat să se potrivească curbei logistice, pe baza ipotezelor funcției logistice, la trei recensăminte separate ale populației statului Statele Unite din America pentru a prezice creșterea viitoare în această țară. Toate cele trei seturi de predicții au eșuat.

În 1924, profesorii Ray Pearl și Lowell J. Reed au folosit modelul Verhulst pentru a prezice o limită superioară de 2 miliarde pentru populația lumii . Această limită a fost depășită în 1930. În 1936, o nouă încercare a Pearl și a asociatei sale, Sophia Gould, a produs o limită superioară de 2,6 miliarde. Această limită a fost depășită în 1955.

O analiză a acestor critici a fost efectuată de profesorul Peter Turchin ( Complicated Population Dynamics , 2003) care, în ciuda tuturor, concluzionează că acest tip de ecuații oferă o structură utilă pentru dinamica unei singure specii (și datorită modelelor generalizate ^[6] ) și poate contribui la modelarea interacțiunilor mai multor specii.

În ciuda criticilor, istoric curba logistică a fost un punct de întâlnire între modelele matematice și sociologice, cum ar fi teoria transformării lui George Land , care folosește conceptul de curbă a. $S.$ ${\ displaystyle S}$ $S.$ pentru a prezice un model business-industrial corect în diferitele scenarii ale unui proces de creștere tehnologică.

Notă

^ (RO) Robert U. Ayres, Transformări tehnologice și unde lungi (PDF), în Institutul Internațional pentru Analiza Sistemelor Aplicate, februarie 1989. Accesat pe 7 iulie 2012 (depus de „Original url 7 iulie 2012). ()
^ (EN) Cesare Marchetti, Kondratiev Revisited - After One Kondratiev Cycle (PDF), în Institutul Internațional pentru Analiza Sistemelor Aplicate, martie 1988. Accesat pe 7 iulie 2012 (depus de 'Original url 7 iulie 2012). ()
^ (EN) Cesare Marchetti, Pervasive Long Waves: Is Human Society Cyclotymic? ( PDF ), în International Institute for Applied Systems Analysis , septembrie 1996. Accesat la 7 iulie 2012 (arhivat din original la 7 iulie 2012) . ()
^ (EN) Arnulf Grübler, Rise and Fall of Infrastructures: Evolution and Dynamics of Technological Change in Transport (PDF), Heidelberg, Physica-Verlag, 1990, p. 305. Adus la 7 iulie 2012 (arhivat din original la 7 iulie 2012) . ISBN 9780387913742 . ()
^ (RO) Revoluții tehnologice și capital financiar Carlota Perez : dinamica bulelor și epocilor de aur , Editura Edward Elgar, 2002, p. 198. ISBN 9781840649222
^ A. Urso, Generalizarea ecuației logistice ( PDF ), pe mathematic.it , www.matematici.it.

Elemente conexe

Concurență interspecifică
Concurență intraspecifică
Ecuația diferențială a lui Fisher , extinderea ecuației logistice la difuzia spațială.
Ecuațiile Lotka-Volterra
Funcția sigmoidă
Legea lui Gompertz
Harta logistică
Modelul Malthus
Funcția Softmax

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere cu funcție logistică

linkuri externe

( EN ) Ecuație logistică , în Encyclopedia Britannica , Encyclopædia Britannica, Inc.

Portal de ecologie și mediu

Portalul de matematică

[ayres-1989-1] (RO) Robert U. Ayres, Transformări tehnologice și unde lungi (PDF), în Institutul Internațional pentru Analiza Sistemelor Aplicate, februarie 1989. Accesat pe 7 iulie 2012 (depus de „Original url 7 iulie 2012). ()

[marchetti-1988-2] (EN) Cesare Marchetti, Kondratiev Revisited - After One Kondratiev Cycle (PDF), în Institutul Internațional pentru Analiza Sistemelor Aplicate, martie 1988. Accesat pe 7 iulie 2012 (depus de 'Original url 7 iulie 2012). ()

[marchetti-1996-3] (EN) Cesare Marchetti, Pervasive Long Waves: Is Human Society Cyclotymic? ( PDF ), în International Institute for Applied Systems Analysis , septembrie 1996. Accesat la 7 iulie 2012 (arhivat din original la 7 iulie 2012) . ()

[grübler-1990-4] (EN) Arnulf Grübler, Rise and Fall of Infrastructures: Evolution and Dynamics of Technological Change in Transport (PDF), Heidelberg, Physica-Verlag, 1990, p. 305. Adus la 7 iulie 2012 (arhivat din original la 7 iulie 2012) . ISBN 9780387913742 . ()

[perez-2002-5] (RO) Revoluții tehnologice și capital financiar Carlota Perez : dinamica bulelor și epocilor de aur , Editura Edward Elgar, 2002, p. 198. ISBN 9781840649222

[6] A. Urso, Generalizarea ecuației logistice ( PDF ), pe mathematic.it , www.matematici.it.

[1]

[2]

[3] au

[4]

[5] a

[6]

V · D · M Interacțiune biologică și simbioză
Neutru sau semineutru	Neutralitatea · Amensalismo ( alelopatie ) · comensualitate ( Inquiline · Foresi · Metabiosi )
Nu neutru	Concurență ( intraspecifică · interspecifică ) · Exploatare ( Predare · erbivoră · parazitism · Parassitoidismo ) · Mutualismo ( protocooperare )
Alte articole	Aposymbiotic · intraspecifice Raport · interspecifice Raport · Coevoluție · cursa evolutiv arme · Teoria endosymbiotic · Facilitarea · Eusociality · imitarea ( Criptismo · aposematism · Omocromia · imitarea moleculară ) · Vector