e (constanta matematica)

e (numărul lui Euler)
Simbol	Și
Valoare	2.71828 18284 59045 23536 ... (secvența A001113 a OEIS )
Originea numelui	Euler
Fracție continuă	[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, ...] (secvența A003417 a OEIS)
Împreună	numere transcendente
Constantele corelate	Constanta lui Gelfond, constanta Omega
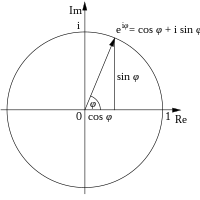Constanta e apare în formula lui Euler, una dintre cele mai importante identități matematice.

În matematică numărul $Și$ ${\ displaystyle e}$ $Și$ este o constantă matematică a cărei valoare aproximativă la 12 zecimale este $2{,}718281828459$ ${\ displaystyle 2 {,} 718281828459}$ ${\ displaystyle 2 {,} 718281828459}$ . Este baza funcției exponențiale $e^{x}$ ${\ displaystyle e ^ {x}}$ $și ^ x$ și logaritmul natural . Poate fi definit în diferite moduri, dintre care cel mai comun este ca limită de succesiune $(1+1/n)^{n}$ ${\ displaystyle (1 + 1 / n) ^ {n}}$ ${\ displaystyle (1 + 1 / n) ^ {n}}$ a tinde spre $n$ ${\ displaystyle n}$ $n$ la infinit . Împreună cu π este cea mai importantă constantă matematică, datorită prezenței sale în multe formule aparent fără legătură.

Este un număr transcendent și, prin urmare, irațional , iar prin formula lui Euler este legat de funcțiile trigonometrice . În arena internațională, numărul $Și$ ${\ displaystyle e}$ $Și$ se numește numărul lui Euler , în timp ce în Italia este numit și numărul lui Napier .

Definiții

Numarul $Și$ ${\ displaystyle e}$ $Și$ poate fi definit în unul din următoarele moduri:

ca valoare a limitei

e:=\lim _{n\to \infty }{\left(1+{\frac {1}{n}}\right)}^{n}

{\ displaystyle e: = \ lim _ {n \ to \ infty} {\ left (1 + {\ frac {1} {n}} \ right)} ^ {n}}

e: = \ lim _ {{n \ to \ infty}} {\ left (1 + {\ frac {1} {n}} \ right)} ^ {n}

;

ca seria

e:=\sum _{n=0}^{\infty }{1 \over n!}={1 \over 0!}+{1 \over 1!}+{1 \over 2!}+{1 \over 3!}+{1 \over 4!}+\cdots

{\ displaystyle e: = \ sum _ {n = 0} ^ {\ infty} {1 \ over n!} = {1 \ over 0!} + {1 \ over 1!} + {1 \ over 2!} + {1 \ peste 3!} + {1 \ peste 4!} + \ Cdots}

e: = \ sum _ {{n = 0}} ^ {\ infty} {1 \ over n!} = {1 \ over 0!} + {1 \ over 1!} + {1 \ over 2!} + {1 \ peste 3!} + {1 \ peste 4!} + \ Cdots

unde este $n!$ ${\ displaystyle n!}$ $n!$ este factorialul numărului natural $n$ ${\ displaystyle n}$ $n$ .

O demonstrație a echivalenței acestor definiții este dată mai jos. Definițiile sunt utilizate în mod similar în definiția funcției exponențiale .

Un mod alternativ (non-standard) de definire $Și$ ${\ displaystyle e}$ $Și$ implică ecuații diferențiale : numărul Napier poate fi definit ca valoarea în $x=1$ ${\ displaystyle x = 1}$ $x = 1$ a funcției $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ soluție unică a problemei Cauchy dată de ecuația diferențială $f^{\prime }(x)=f(x)$ ${\ displaystyle f ^ {\ prime} (x) = f (x)}$ $f ^ {\ prime} (x) = f (x)$ cu condiții inițiale $f(0)=1$ ${\ displaystyle f (0) = 1}$ $f (0) = 1$ .

Proprietate

Număr irațional și transcendent

Același subiect în detaliu: Dovada iraționalității e și Dovada transcendenței e .

Numarul $Și$ ${\ displaystyle e}$ $Și$ este irațional , mai exact un număr transcendent , adică nu există o ecuație algebrică cu coeficienți raționali care să o admită ca soluție. Acesta a fost primul număr care s-a dovedit a fi transcendent fără a fi construit pentru a fi plasat în setul de numere reale non-algebrice, așa cum se întâmpla anterior pentru constanta Liouville . O demonstrație a iraționalității lui e a fost dată de Charles Hermite în 1873 . Se presupune că este un număr normal .

Formula lui Euler

Constanta $Și$ ${\ displaystyle e}$ $Și$ apare în formula lui Euler , una dintre cele mai importante identități din matematică:

e^{ix}=\cos(x)+i\,\mathrm {sin} (x),

{\ displaystyle e ^ {ix} = \ cos (x) + i \, \ mathrm {sin} (x),}

e ^ {{ix}} = \ cos (x) + i \, {\ mathrm {sin}} (x),

unde este $the$ ${\ displaystyle i}$ $the$ indică unitatea imaginară . Cazul special cu $x=\pi$ ${\ displaystyle x = \ pi}$ $x = \ pi$ este cunoscută sub numele de identitatea lui Euler :

e^{i\pi }+1=0;

{\ displaystyle e ^ {i \ pi} + 1 = 0;}

și ^ {{i \ pi}} + 1 = 0;

această egalitate a fost numită de Richard Feynman „bijuteria lui Euler”.

Fracție continuă

Dezvoltarea $Și$ ${\ displaystyle e}$ $Și$ ca o fracție continuă infinită este exprimată prin următoarea configurație:

e=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,\ldots ].

{\ displaystyle e = [2; 1,2,1,1,4,1,1,6,1,1,8,1,1,10, \ ldots].}

e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, \ ldots].

Prin trunchierea fracției continue, aproximările raționale ale $Și$ ${\ displaystyle e}$ $Și$ , dintre care primele (nu întregi) sunt $3,\ 8/3,\ 11/4,\ 19/7$ ${\ displaystyle 3, \ 8/3, \ 11/4, \ 19/7}$ $3, \ 8/3, \ 11/4, \ 19/7$ .

Proprietăți analitice

Numarul $Și$ ${\ displaystyle e}$ $Și$ este punctul central al comutării exponențierii. Se dau toate perechile $(x,y)$ ${\ displaystyle (x, y)}$ $(X y)$ pentru care $x^{y}=y^{x}$ ${\ displaystyle x ^ {y} = y ^ {x}}$ $x ^ {y} = y ^ {x}$ . Pe lângă cazul banal $x=y$ ${\ displaystyle x = y}$ $x = y$ , singura pereche întreagă (și rațională) pentru care deține proprietatea este formată din numerele 2 și 4, dar este valabilă și pentru perechi iraționale infinite distribuite de-a lungul unei curbe în primul cadran, asimptotic la liniile drepte $x=1$ ${\ displaystyle x = 1}$ $x = 1$ Și $y=1$ ${\ displaystyle y = 1}$ $y = 1$ . Această curbă și linia dreaptă $y=x$ ${\ displaystyle y = x}$ $y = x$ se intersectează în punct $(e,e)$ ${\ displaystyle (e, e)}$ $(si si)$ . Încă pe funcții exponențiale, rădăcina $X$ ${\ displaystyle x}$ $X$ -thth din $X$ ${\ displaystyle x}$ $X$ , adică $x^{\frac {1}{x}}$ ${\ displaystyle x ^ {\ frac {1} {x}}}$ $x ^ {{{\ frac {1} {x}}}}$ , are maxim pentru $x=e$ ${\ displaystyle x = e}$ $x = e$ iar exponențialul $X$ ${\ displaystyle x}$ $X$ -thth din $X$ ${\ displaystyle x}$ $X$ , adică $x^{x}$ ${\ displaystyle x ^ {x}}$ $x ^ {x}$ , are minim pentru $x={\frac {1}{e}}$ ${\ displaystyle x = {\ frac {1} {e}}}$ $x = {\ frac {1} {e}}$ .

Istorie

De-a lungul anilor numărul

Și

{\ displaystyle e}

Și

a fost aproximat la o precizie de milioane de zecimale.

Prima referire la $Și$ ${\ displaystyle e}$ $Și$ în literatură datează din 1618 și este cuprins în tabelul unui apendice al unei lucrări despre logaritmi de John Napier . Tabelul nu arată constanta, ci o listă de logaritmi naturali care pot fi calculați începând de la constantă. Tabelul pare să fi fost scris de William Oughtred . Prima expresie a $Și$ ${\ displaystyle e}$ $Și$ ca o constantă a fost găsită de Jakob Bernoulli :

\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}

{\ displaystyle \ lim _ {n \ to \ infty} \ left (1 + {\ frac {1} {n}} \ right) ^ {n}}

\ lim _ {{n \ to \ infty}} \ left (1 + {\ frac {1} {n}} \ right) ^ {n}

Din această expresie este dificil să se obțină o valoare numerică bună pentru constantă.

Primul său citat, reprezentat cu litera $b$ ${\ displaystyle b}$ $b$ apare în două scrisori de la Gottfried Leibniz către Christiaan Huygens , datate 1690 și 1691 . Leonhard Euler a început să folosească scrisoarea $Și$ ${\ displaystyle e}$ $Și$ pentru constanta din 1727 și prima utilizare a $Și$ ${\ displaystyle e}$ $Și$ apare în Mechanica lui Euler ( 1736 ). În anii următori, unii cercetători au folosit scrisoarea $c$ ${\ displaystyle c}$ $c$ , apoi utilizarea $Și$ ${\ displaystyle e}$ $Și$ a devenit mai frecventă. Astăzi scrisoarea $Și$ ${\ displaystyle e}$ $Și$ este simbolul definitiv pentru a indica numărul lui Napier.

Nu se cunosc motivele care au dus la alegerea scrisorii $Și$ ${\ displaystyle e}$ $Și$ , putem presupune că $Și$ ${\ displaystyle e}$ $Și$ a fost ales pentru că a fost inițiala cuvântului exponențial . ^[1] Un alt motiv este că $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ , $c$ ${\ displaystyle c}$ $c$ , Și $d$ ${\ displaystyle d}$ $d$ au fost folosite frecvent pentru alte obiecte matematice și $Și$ ${\ displaystyle e}$ $Și$ a fost prima literă neutilizată a alfabetului latin. Este puțin probabil ca Euler să aleagă litera ca inițială a numelui său, deoarece numărul nu era descoperirea sa, era deja cunoscut de matematicienii vremii.

Demonstrarea echivalenței celor două formulări

Următoarea dovadă demonstrează echivalența expansiunii în serii infinite prezentate anterior și expresia limitei studiate de Bernoulli.

Noi definim

s_{n}:=\sum _{k=0}^{n}{\frac {1}{k!}}~,

{\ displaystyle s_ {n}: = \ sum _ {k = 0} ^ {n} {\ frac {1} {k!}} ~,}

s_ {n}: = \ sum _ {{k = 0}} ^ {n} {\ frac {1} {k!}} ~,

t_{n}=\left(1+{\frac {1}{n}}\right)^{n}~.

{\ displaystyle t_ {n} = \ left (1 + {\ frac {1} {n}} \ right) ^ {n} ~.}

t_ {n} = \ left (1 + {\ frac {1} {n}} \ right) ^ {n} ~.

Din teorema binomului ,

t_{n}=\sum _{k=0}^{n}{n \choose k}{\frac {1}{n^{k}}}=1+1+\sum _{k=2}^{n}{\frac {n(n-1)(n-2)\cdots (n-(k-1))}{k!\,n^{k}}}

{\ displaystyle t_ {n} = \ sum _ {k = 0} ^ {n} {n \ alege k} {\ frac {1} {n ^ {k}}} = 1 + 1 + \ sum _ {k = 2} ^ {n} {\ frac {n (n-1) (n-2) \ cdots (n- (k-1))} {k! \, N ^ {k}}}}

t_ {n} = \ sum _ {{k = 0}} ^ {n} {n \ alege k} {\ frac {1} {n ^ {k}}} = 1 + 1 + \ sum _ {{k = 2}} ^ {n} {\ frac {n (n-1) (n-2) \ cdots (n- (k-1))} {k! \, N ^ {k}}}

=1+1+{\frac {1}{2!}}\left(1-{\frac {1}{n}}\right)+{\frac {1}{3!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)+\cdots +{\frac {1}{n!}}\left(1-{\frac {1}{n}}\right)\cdots \left(1-{\frac {n-1}{n}}\right)\leq s_{n}

{\ displaystyle = 1 + 1 + {\ frac {1} {2!}} \ left (1 - {\ frac {1} {n}} \ right) + {\ frac {1} {3!}} \ left (1 - {\ frac {1} {n}} \ right) \ left (1 - {\ frac {2} {n}} \ right) + \ cdots + {\ frac {1} {n!}} \ left (1 - {\ frac {1} {n}} \ right) \ cdots \ left (1 - {\ frac {n-1} {n}} \ right) \ leq s_ {n}}

= 1 + 1 + {\ frac {1} {2!}} \ Left (1 - {\ frac {1} {n}} \ right) + {\ frac {1} {3!}} \ Left (1 - {\ frac {1} {n}} \ right) \ left (1 - {\ frac {2} {n}} \ right) + \ cdots + {\ frac {1} {n!}} \ left ( 1 - {\ frac {1} {n}} \ right) \ cdots \ left (1 - {\ frac {n-1} {n}} \ right) \ leq s_ {n}

astfel încât

\limsup _{n\to \infty }t_{n}\leq \limsup _{n\to \infty }s_{n}=e~.

{\ displaystyle \ limsup _ {n \ to \ infty} t_ {n} \ leq \ limsup _ {n \ to \ infty} s_ {n} = e ~.}

\ limsup _ {{n \ to \ infty}} t_ {n} \ leq \ limsup _ {{n \ to \ infty}} s_ {n} = e ~.

Limita superioară sau limsup ar trebui folosită aici, deoarece nu se știe încă asta $t_{n}$ ${\ displaystyle t_ {n}}$ $t_n$ converge de fapt. Acum, pentru cealaltă direcție, observăm că din expresia de mai sus a $t_{n}$ ${\ displaystyle t_ {n}}$ $t_n$ , de sine $2\leq m\leq n$ ${\ displaystyle 2 \ leq m \ leq n}$ $2 \ leq m \ leq n$ , avem

1+1+{\frac {1}{2!}}\left(1-{\frac {1}{n}}\right)+\cdots +{\frac {1}{m!}}\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)\cdots \left(1-{\frac {m-1}{n}}\right)\leq t_{n}

{\ displaystyle 1 + 1 + {\ frac {1} {2!}} \ left (1 - {\ frac {1} {n}} \ right) + \ cdots + {\ frac {1} {m!} } \ left (1 - {\ frac {1} {n}} \ right) \ left (1 - {\ frac {2} {n}} \ right) \ cdots \ left (1 - {\ frac {m- 1} {n}} \ right) \ leq t_ {n}}

1 + 1 + {\ frac {1} {2!}} \ Left (1 - {\ frac {1} {n}} \ right) + \ cdots + {\ frac {1} {m!}} \ Left (1 - {\ frac {1} {n}} \ right) \ left (1 - {\ frac {2} {n}} \ right) \ cdots \ left (1 - {\ frac {m-1} { n}} \ right) \ leq t_ {n}

Fix $m$ ${\ displaystyle m}$ $m$ se tensionează $n$ ${\ displaystyle n}$ $n$ la nesfârșit. Noi obținem

s_{m}=1+1+{\frac {1}{2!}}+\cdots +{\frac {1}{m!}}\leq \liminf _{n\to \infty }t_{n}

{\ displaystyle s_ {m} = 1 + 1 + {\ frac {1} {2!}} + \ cdots + {\ frac {1} {m!}} \ leq \ liminf _ {n \ to \ infty} t_ {n}}

s_ {m} = 1 + 1 + {\ frac {1} {2!}} + \ cdots + {\ frac {1} {m!}} \ leq \ liminf _ {{n \ to \ infty}} t_ {n}

(din nou, trebuie să folosim limita inferioară sau liminf deoarece nu este încă garantat acest lucru $t_{n}$ ${\ displaystyle t_ {n}}$ $t_n$ converge).

Acum, având în vedere inegalitatea anterioară, $m$ ${\ displaystyle m}$ $m$ se apropie de infinit și îl pune pe acesta din urmă împreună cu cealaltă inegalitate; de la care:

\limsup _{n\to \infty }t_{n}\leq e\leq \liminf _{n\to \infty }t_{n}\leq \limsup _{n\to \infty }t_{n}

{\ displaystyle \ limsup _ {n \ to \ infty} t_ {n} \ leq e \ leq \ liminf _ {n \ to \ infty} t_ {n} \ leq \ limsup _ {n \ to \ infty} t_ { n}}

\ limsup _ {{n \ to \ infty}} t_ {n} \ leq e \ leq \ liminf _ {{n \ to \ infty}} t_ {n} \ leq \ limsup _ {{n \ to \ infty} } t_ {n}

Aceasta completează dovada.

Reprezentare stochastică

Pe lângă reprezentările analitice exacte de calculat $Și$ ${\ displaystyle e}$ $Și$ , există metode stochastice de estimare a acestuia. Una dintre acestea începe de la o succesiune infinită de variabile aleatoare independente $X_{1},X_{2},\ldots ,X_{n}$ ${\ displaystyle X_ {1}, X_ {2}, \ ldots, X_ {n}}$ ${\ displaystyle X_ {1}, X_ {2}, \ ldots, X_ {n}}$ distribuite uniform în interval $[0,1]$ ${\ displaystyle [0,1]}$ $[0,1]$ . Este $K.$ ${\ displaystyle K}$ $K.$ numărul de sume parțiale de variabile $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ care sunt strict mai mici decât $1$ ${\ displaystyle 1}$ $1$ , punând:

V={\frac {1}{K}}\sum _{i=0}^{K}n_{i},

{\ displaystyle V = {\ frac {1} {K}} \ sum _ {i = 0} ^ {K} n_ {i},}

{\ displaystyle V = {\ frac {1} {K}} \ sum _ {i = 0} ^ {K} n_ {i},}

unde este $n_{i}=\min(n:X_{1}+X_{2}+\ldots +X_{n}>1),$ ${\ displaystyle n_ {i} = \ min (n: X_ {1} + X_ {2} + \ ldots + X_ {n}> 1),}$ ${\ displaystyle n_ {i} = \ min (n: X_ {1} + X_ {2} + \ ldots + X_ {n}> 1),}$ apoi valoarea scontată $V.$ ${\ displaystyle V}$ $V.$ este constanta $Și$ ${\ displaystyle e}$ $Și$ .

Notă

^ Carl B. Boyer, History of Mathematics , Mondadori, ISBN 88-04-33431-2 .

Bibliografie

Eli Maor: e: Povestea unui număr , ISBN 0-691-05854-7
Paolo Marcellini , Carlo Sbordone Mathematical Analysis One , Liguori Editore, Napoli, ISBN 88-207-2819-2 , 1998, paragrafele 31 și 102.

Elemente conexe

Primele 100.000 de cifre ale e

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere pe e (constantă matematică)

linkuri externe

( RO ) Numărul e (istoric) , pe www-gap.dcs.st-and.ac.uk . Adus la 7 septembrie 2004 (arhivat din original la 14 septembrie 2004) .
Primul milion și primele două milioane de zecimale ale numărului și

Controlul autorității	LCCN (EN) sh93008168 · GND (DE) 4150966-3

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Carl B. Boyer, History of Mathematics , Mondadori, ISBN 88-04-33431-2 .

[1]