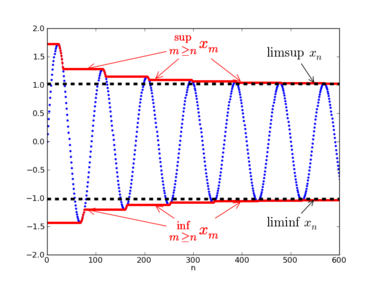
Limita superioară și limita inferioară

Limita superioară și limita inferioară. Succesiunea

x_{n}

{\ displaystyle x_ {n}}

x_ {n}

este afișat în albastru; cele două curbe roșii se apropie de limitele superioare și inferioare (reprezentate de cele două liniuțe negre). În acest caz, limita superioară este strict mai mare decât cea inferioară. În general, cele două limite sup și inf coincid dacă și numai dacă secvența este convergentă.

În matematică , sunt luate în considerare două tipuri de construcții, respectiv numite limită inferioară (sau chiar limită minimă ) și limită superioară (sau chiar limită maximă ) care sunt mai slabe decât limita una, dar cu implementare mai generală și care pot fi utile pentru adresă diverse probleme despre limite. Cele două noțiuni sunt introduse pentru funcții cu valoare reală , pentru secvențe de mulțimi și, în general, pentru funcții având ca codomain o mulțime parțial ordonată . În cel mai simplu caz al unei succesiuni de numere reale, aceste două noțiuni servesc la „limitarea” intervalului acestei funcții, adică a regiunii în care componentele secvenței sunt „definitiv” localizate.

Limitele inferioare și superioare ale unei secvențe

Având în vedere o succesiune de numere reale $({x_{n}})$ ${\ displaystyle ({x_ {n}})}$ $({x_n})$ , sunt:

{b_{k}}=\sup\{x_{k},x_{k+1},\dots \}\quad k=1,2,\dots

{\ displaystyle {b_ {k}} = \ sup \ {x_ {k}, x_ {k + 1}, \ dots \} \ quad k = 1,2, \ dots}

{b_k} = \ sup \ {x_k, x_ {k + 1}, \ dots \} \ quad k = 1,2, \ dots

\beta =\inf\{b_{1},b_{2},\dots \}

{\ displaystyle \ beta = \ inf \ {b_ {1}, b_ {2}, \ dots \}}

\ beta = \ inf \ {b_1, b_2, \ dots \}

Atunci $\beta$ ${\ displaystyle \ beta}$ $\ beta$ este limita superioară a $({x_{n}})$ ${\ displaystyle ({x_ {n}})}$ $({x_n})$ : ^[1]

\beta =\limsup _{n\rightarrow \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\sup _{m\geq n}x_{m}{\Big )}=\inf\{\,\sup\{\,x_{k}:k\geq n\,\}:n\geq 0\,\}

{\ displaystyle \ beta = \ limsup _ {n \ rightarrow \ infty} x_ {n}: = \ lim _ {n \ to \ infty} {\ Big (} \ sup _ {m \ geq n} x_ {m} {\ Big)} = \ inf \ {\, \ sup \ {\, x_ {k}: k \ geq n \, \}: n \ geq 0 \, \}}

\ beta = \ limsup_ {n \ rightarrow \ infty} x_n: = \ lim_ {n \ to \ infty} \ Big (\ sup_ {m \ geq n} x_m \ Big) = \ inf \ {\, \ sup \ { \, x_k: k \ geq n \, \}: n \ geq 0 \, \}

Am notat asta:

\lim _{k\to \infty }b_{k}=\beta

{\ displaystyle \ lim _ {k \ to \ infty} b_ {k} = \ beta}

\ lim_ {k \ to \ infty} b_k = \ beta

și există o subsecvență ${x_{n_{i}}}$ ${\ displaystyle {x_ {n_ {i}}}}$ ${x_ {n_i}}$ din ${x_{n}}$ ${\ displaystyle {x_ {n}}}$ ${x_n}$ astfel încât:

\lim _{i\to \infty }x_{n_{i}}=\beta

{\ displaystyle \ lim _ {i \ to \ infty} x_ {n_ {i}} = \ beta}

\ lim_ {i \ to \ infty} x_ {n_i} = \ beta

Și $\beta$ ${\ displaystyle \ beta}$ $\ beta$ este cel mai mare număr care se bucură de o astfel de proprietate.

În mod similar, limita inferioară a unei secvențe este definită: ^[2]

\liminf _{n\to \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\inf _{m\geq n}x_{m}{\Big )}=\sup\{\,\inf\{\,x_{m}:m\geq n\,\}:n\geq 0\,\}

{\ displaystyle \ liminf _ {n \ to \ infty} x_ {n}: = \ lim _ {n \ to \ infty} {\ Big (} \ inf _ {m \ geq n} x_ {m} {\ Big )} = \ sup \ {\, \ inf \ {\, x_ {m}: m \ geq n \, \}: n \ geq 0 \, \}}

\ liminf_ {n \ to \ infty} x_n: = \ lim_ {n \ to \ infty} \ Big (\ inf_ {m \ geq n} x_m \ Big) = \ sup \ {\, \ inf \ {\, x_m : m \ geq n \, \}: n \ geq 0 \, \}

Uneori notația este utilizată pentru a indica limitele superioare și inferioare:

\varliminf _{n\to \infty }x_{n}:=\liminf _{n\to \infty }x_{n}\quad \varlimsup _{n\to \infty }x_{n}:=\limsup _{n\to \infty }x_{n}

{\ displaystyle \ varliminf _ {n \ to \ infty} x_ {n}: = \ liminf _ {n \ to \ infty} x_ {n} \ quad \ varlimsup _ {n \ to \ infty} x_ {n}: = \ limsup _ {n \ to \ infty} x_ {n}}

\ varliminf_ {n \ to \ infty} x_n: = \ liminf_ {n \ to \ infty} x_n \ quad \ varlimsup_ {n \ to \ infty} x_n: = \ limsup_ {n \ to \ infty} x_n

Dacă elementele secvenței aparțin unui set parțial ordonat din care există extremele superioare și inferioare, limitele superioară și inferioară există întotdeauna și avem:

-\limsup _{n\rightarrow \infty }(-x_{n})=\liminf _{n\to \infty }x_{n}

{\ displaystyle - \ limsup _ {n \ rightarrow \ infty} (- x_ {n}) = \ liminf _ {n \ to \ infty} x_ {n}}

- \ limsup_ {n \ rightarrow \ infty} (- x_n) = \ liminf_ {n \ to \ infty} x_n

Dacă succesiunea ${x_{n}}$ ${\ displaystyle {x_ {n}}}$ ${x_n}$ converge avem: ^[2]

\limsup _{n\to \infty }(x_{n})=\liminf _{n\to \infty }(x_{n})=\lim _{n\to \infty }x_{n}

{\ displaystyle \ limsup _ {n \ to \ infty} (x_ {n}) = \ liminf _ {n \ to \ infty} (x_ {n}) = \ lim _ {n \ to \ infty} x_ {n }}

{\ displaystyle \ limsup _ {n \ to \ infty} (x_ {n}) = \ liminf _ {n \ to \ infty} (x_ {n}) = \ lim _ {n \ to \ infty} x_ {n }}

Noțiunile de limite inferioare și superioare sunt legate de big-O , deoarece astfel de entități oferă restricții asupra valorilor secvenței numai la limită. Alternativ, după introducerea conceptelor de valoare limită și clasă limită, limitele superioare și inferioare ale unei secvențe pot fi definite pur și simplu ca maxim și minim al clasei limită a acestei secvențe, care se arată că există întotdeauna.

Limitele inferioare și superioare ale unei funcții reale

Este $f:A\rightarrow \mathbb {R}$ ${\ displaystyle f: A \ rightarrow \ mathbb {R}}$ $f: A \ rightarrow \ R$ o funcție definită într-un subset $LA$ ${\ displaystyle A}$ $LA$ fie a oricărui spațiu topologic $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ un punct de acumulare e $I(x_{0})$ ${\ displaystyle I (x_ {0})}$ $Eu (x_ {0})$ familia cartierelor din $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ în $LA$ ${\ displaystyle A}$ $LA$ , cu $U\in I(x_{0})$ ${\ displaystyle U \ in I (x_ {0})}$ ${\ displaystyle U \ in I (x_ {0})}$ . Limita inferioară a unei funcții reale pentru $x\rightarrow x_{0}$ ${\ displaystyle x \ rightarrow x_ {0}}$ $x \ rightarrow x_0$ este definit ca:

\liminf _{x\to x_{0}}f(x)=\sup _{U}\,\left[\inf _{x\in (U\cap A\setminus \{x_{0}\})}f(x)\right]=\sup\{\,\inf\{f(x)|\;x\in (U\cap A\setminus \{x_{0}\})\,\}\,\}

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = \ sup _ {U} \, \ left [\ inf _ {x \ in (U \ cap A \ setminus \ {x_ {0 } \})} f (x) \ right] = \ sup \ {\, \ inf \ {f (x) | \; x \ in (U \ cap A \ setminus \ {x_ {0} \}) \ , \} \, \}}

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = \ sup _ {U} \, \ left [\ inf _ {x \ in (U \ cap A \ setminus \ {x_ {0 } \})} f (x) \ right] = \ sup \ {\, \ inf \ {f (x) | \; x \ in (U \ cap A \ setminus \ {x_ {0} \}) \ , \} \, \}}

Intuitiv, limita inferioară a $f$ ${\ displaystyle f}$ $f$ pentru $X$ ${\ displaystyle x}$ $X$ → $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ este valoarea maximă, ca vecinătate a $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ , de cea mai mică valoare pe care funcția o asumă într-un singur cartier.

Limita superioară a unei funcții reale pentru $x\rightarrow x_{0}$ ${\ displaystyle x \ rightarrow x_ {0}}$ $x \ rightarrow x_0$ este definit în mod similar:

\limsup _{x\to x_{0}}f(x)=\inf _{U}\,\left[\sup _{x\in (U\cap A\setminus \{x_{0}\})}f(x)\right]=\inf\{\,\sup\{f(x)|x\in (U\cap A\setminus \{x_{0}\})\,\}\,\}

{\ displaystyle \ limsup _ {x \ to x_ {0}} f (x) = \ inf _ {U} \, \ left [\ sup _ {x \ in (U \ cap A \ setminus \ {x_ {0 } \})} f (x) \ right] = \ inf \ {\, \ sup \ {f (x) | x \ in (U \ cap A \ setminus \ {x_ {0} \}) \, \ } \, \}}

{\ displaystyle \ limsup _ {x \ to x_ {0}} f (x) = \ inf _ {U} \, \ left [\ sup _ {x \ in (U \ cap A \ setminus \ {x_ {0 } \})} f (x) \ right] = \ inf \ {\, \ sup \ {f (x) | x \ in (U \ cap A \ setminus \ {x_ {0} \}) \, \ } \, \}}

Prin urmare, corespunde celei mai mici valori dintre valorile maxime pe care funcția le asumă în fiecare vecinătate a punctului.

Caracteristici și proprietăți

Prin exploatarea definițiilor algoritmilor limită superioară și inferioară, se aplică aceste caracteristici ale celor două limite, adică

\liminf _{x\to x_{0}}f(x)=m\in \mathbb {R} \iff \left\{{\begin{matrix}\forall \varepsilon \!>\!0\;\exists \,U_{\varepsilon }(x_{0})|\;\forall x\in (U_{\varepsilon }\!\cap \!A\!\setminus \!\{x_{0}\})\implies f(x)>m-\varepsilon \\\!\!\!\!\!\!\!\!\!\!\!\!\!\forall \varepsilon \!>\!0\;\forall \,U_{\varepsilon }(x_{0}),\exists x\in (U_{\varepsilon }\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)<m+\varepsilon \end{matrix}}\right.

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = m \ in \ mathbb {R} \ if \ left \ {{\ begin {matrix} \ forall \ varepsilon \!> \! 0 \; \ există \, U _ {\ varepsilon} (x_ {0}) | \; \ forall x \ in (U _ {\ varepsilon} \! \ cap \! A \! \ setminus \! \ {x_ { 0} \}) \ implică f (x)> m- \ varepsilon \\\! \! \! \! \! \! \! \! \! \! \! \! \! \ Forall \ varepsilon \! > \! 0 \; \ forall \, U _ {\ varepsilon} (x_ {0}), \ există x \ in (U _ {\ varepsilon} \! \ Cap \! A \! \ Setminus \! \ { X_ {0} \}) | \; f (x) <m + \ varepsilon \ end {matrix}} \ right.}

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = m \ in \ mathbb {R} \ if \ left \ {{\ begin {matrix} \ forall \ varepsilon \!> \! 0 \; \ există \, U _ {\ varepsilon} (x_ {0}) | \; \ forall x \ in (U _ {\ varepsilon} \! \ cap \! A \! \ setminus \! \ {x_ { 0} \}) \ implică f (x)> m- \ varepsilon \\\! \! \! \! \! \! \! \! \! \! \! \! \! \ Forall \ varepsilon \! > \! 0 \; \ forall \, U _ {\ varepsilon} (x_ {0}), \ există x \ in (U _ {\ varepsilon} \! \ Cap \! A \! \ Setminus \! \ { X_ {0} \}) | \; f (x) <m + \ varepsilon \ end {matrix}} \ right.}

Prima linie afirmă că cu siguranță orice nivel inferior celui $m$ ${\ displaystyle m}$ $m$ este impracticabil, adică un întreg înconjurător al $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ are imagini mai mari decât $m-\varepsilon$ ${\ displaystyle m- \ varepsilon}$ $m - \ varepsilon$ (corespunzând proprietății de a fi o extremă superioară); al doilea care se găsește în fiecare cartier $X$ ${\ displaystyle x}$ $X$ cu o imagine apropiată în mod arbitrar $m$ ${\ displaystyle m}$ $m$ (datorită faptului că este o extremă inferioară).

În cazul infinit, aceste proprietăți sunt în schimb:

\liminf _{x\to x_{0}}f(x)=-\infty \iff \forall K\!>\!0\;\forall \,U(x_{0}),\exists x\in (U\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)<-K

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = - \ infty \ iff \ forall K \!> \! 0 \; \ forall \, U (x_ {0}), \ există x \ in (U \! \ cap \! A \! \ setminus \! \ {x_ {0} \}) | \; f (x) <- K}

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = - \ infty \ iff \ forall K \!> \! 0 \; \ forall \, U (x_ {0}), \ există x \ in (U \! \ cap \! A \! \ setminus \! \ {x_ {0} \}) | \; f (x) <- K}

\liminf _{x\to x_{0}}f(x)=+\infty \iff \forall K\!>\!0\;\exists \,U(x_{0}),\forall x\in (U\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)>K

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = + \ infty \ iff \ forall K \!> \! 0 \; \ există \, U (x_ {0}), \ forall x \ in (U \! \ cap \! A \! \ setminus \! \ {x_ {0} \}) | \; f (x)> K}

{\ displaystyle \ liminf _ {x \ to x_ {0}} f (x) = + \ infty \ iff \ forall K \!> \! 0 \; \ există \, U (x_ {0}), \ forall x \ in (U \! \ cap \! A \! \ setminus \! \ {x_ {0} \}) | \; f (x)> K}

Proprietățile pentru legătura maximă sunt obținute în mod analog.

Mai mult, spre deosebire de limită, limitele inferioară și superioară există întotdeauna, deoarece acestea sunt calculate cu algoritmi de limită superioară și inferioară pe seturi reale . De asemenea, este valabil că:

\liminf _{x\rightarrow x_{0}}f(x)\leq \limsup _{x\rightarrow x_{0}}f(x)

{\ displaystyle \ liminf _ {x \ rightarrow x_ {0}} f (x) \ leq \ limsup _ {x \ rightarrow x_ {0}} f (x)}

\ liminf_ {x \ rightarrow x_0} f (x) \ leq \ limsup_ {x \ rightarrow x_0} f (x)

iar egalitatea există dacă și numai dacă există în $\mathbb {R} \cup \{-\infty ,+\infty \}$ ${\ displaystyle \ mathbb {R} \ cup \ {- \ infty, + \ infty \}}$ $\ mathbb {R} \ cup \ {- \ infty, + \ infty \}$ limita $\lim _{x\rightarrow x_{0}}f(x)$ ${\ displaystyle \ lim _ {x \ rightarrow x_ {0}} f (x)}$ $\ lim_ {x \ rightarrow x_0} f (x)$ , care va fi egală cu valoarea comună a $\liminf$ ${\ displaystyle \ liminf}$ $\ liminf$ Și $\limsup$ ${\ displaystyle \ limsup}$ $\ limsup$ .

Convergența secvențelor numerelor reale

Se observă că definițiile precedente au sens în orice set parțial ordonat în care există extremele superioare și inferioare . Acest lucru duce la extinderea definițiilor la secvențe care au componentele în medii mai „exotice” ale setului de numere reale. În fiecare rețea completă există suportul și inful oricărui subset: prin urmare, este deosebit de interesant să se ia în considerare limitele inferioară și superioară ale secvențelor de elemente ale rețelelor complete.

De asemenea, se observă că mulțimea numerelor reale $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ nu constituie o rețea completă, dar completitudinea sa se obține prin adăugarea infinitului negativ și pozitiv la acesta: de fapt, mulțimea $[-\infty ,\infty ]$ ${\ displaystyle [- \ infty, \ infty]}$ $[- \ infty, \ infty]$ constituie un întreg complet ordonat complet .

În acest mediu o succesiune $\{x_{n}:n\in \mathbb {N} \}$ ${\ displaystyle \ {x_ {n}: n \ in \ mathbb {N} \}}$ $\ {x_n: n \ in \ mathbb {N} \}$ converge dacă și numai dacă $\liminf x_{n}=\limsup x_{n}$ ${\ displaystyle \ liminf x_ {n} = \ limsup x_ {n}}$ $\ liminf x_n = \ limsup x_n$ , și dacă da $\lim x_{n}$ ${\ displaystyle \ lim x_ {n}}$ $\ lim x_n$ este egală cu valoarea lor comună (se observă că atunci când operează în solo $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ , divergența a nu este luată în considerare $-\infty$ ${\ displaystyle - \ infty}$ $- \ infty$ oa $+\infty$ ${\ displaystyle + \ infty}$ $+ \ infty$ ).

De exemplu, luați în considerare secvența dată de $x_{n}=\sin n$ ${\ displaystyle x_ {n} = \ sin n}$ $x_n = \ sin n$ . În virtutea faptului că pi este un număr irațional , se arată că $\liminf x_{n}=-1$ ${\ displaystyle \ liminf x_ {n} = - 1}$ $\ liminf x_n = -1$ Și $\limsup x_{n}=+1$ ${\ displaystyle \ limsup x_ {n} = + 1}$ $\ limsup x_n = +1$ .

De sine $I\equiv \liminf x_{n}$ ${\ displaystyle I \ equiv \ liminf x_ {n}}$ $I \ equiv \ liminf x_n$ Și $S\equiv \limsup x_{n}$ ${\ displaystyle S \ equiv \ limsup x_ {n}}$ $S \ equiv \ limsup x_n$ , apoi intervalul $[I,S]$ ${\ displaystyle [I, S]}$ $[ESTE]$ este posibil să nu conțină niciunul dintre numere $x_{n}$ ${\ displaystyle x_ {n}}$ $x_ {n}$ , dar fiecare extensie chiar foarte mică, dar fixă $[I-\epsilon ,S+\epsilon ]$ ${\ displaystyle [I- \ epsilon, S + \ epsilon]}$ $[I- \ epsilon, S + \ epsilon]$ (dependent de un $\epsilon >0$ ${\ displaystyle \ epsilon> 0}$ $\ epsilon> 0$ „în mod arbitrar mic”) conține $x_{n}$ ${\ displaystyle x_ {n}}$ $x_ {n}$ , cel mult cu excepția unui set finit de indici n . De fapt intervalul $[I,S]$ ${\ displaystyle [I, S]}$ $[ESTE]$ este cea mai mică gamă închisă cu această proprietate.

Un exemplu preluat din teoria numerelor se referă:

\liminf _{n}(p_{n+1}-p_{n})

{\ displaystyle \ liminf _ {n} (p_ {n + 1} -p_ {n})}

\ liminf_n (p_ {n + 1} -p_n)

unde cu $p_{n}$ ${\ displaystyle p_ {n}}$ $p_n$ se notează al doilea număr prim . Valoarea acestei limite inferioare a fost conjecturată a fi 2 (aceasta este conjectura primelor gemene ), dar până acum nici nu s-a dovedit că această limită este finită.

Secvențe de seturi

Întreg părțile $P(X)$ ${\ displaystyle P (X)}$ $P (X)$ a unui set $X$ ${\ displaystyle X}$ $X$ constituie o rețea completă și uneori este util să se ia în considerare limitele superioare și inferioare ale secvențelor din $P(X)$ ${\ displaystyle P (X)}$ $P (X)$ , adică secvențe de subseturi de $X$ ${\ displaystyle X}$ $X$ . De sine $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ este o astfel de succesiune, apoi un element $la$ ${\ displaystyle a}$ $la$ din $X$ ${\ displaystyle X}$ $X$ aparține lui $\liminf X_{n}$ ${\ displaystyle \ liminf X_ {n}}$ $\ liminf X_n$ dacă și numai dacă există un întreg natural $n_{0}$ ${\ displaystyle n_ {0}}$ $n_ {0}$ astfel încât $la$ ${\ displaystyle a}$ $la$ aparține lui $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ pentru toți $n>n_{0}$ ${\ displaystyle n> n_ {0}}$ $n> n_0$ . Elementul $la$ ${\ displaystyle a}$ $la$ aparține lui $\limsup X_{n}$ ${\ displaystyle \ limsup X_ {n}}$ $\ limsup X_n$ dacă și numai dacă pentru orice întreg natural $n_{0}$ ${\ displaystyle n_ {0}}$ $n_ {0}$ există un indice $n>n_{0}$ ${\ displaystyle n> n_ {0}}$ $n> n_0$ astfel încât $la$ ${\ displaystyle a}$ $la$ aparține lui $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ . Cu alte cuvinte, $\limsup X_{n}$ ${\ displaystyle \ limsup X_ {n}}$ $\ limsup X_n$ constă din acele elemente găsite în seturi de formular $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ pentru o infinitate de n , în timp ce $\liminf X_{n}$ ${\ displaystyle \ liminf X_ {n}}$ $\ liminf X_n$ constă din acele elemente care sunt excluse cel mult dintr-un număr finit de $X_{n}$ ${\ displaystyle X_ {n}}$ $X_ {n}$ .

Folosind notațiile obișnuite ale teoriei mulțimilor , cea mai mică dintre o succesiune de mulțimi este intersecția numărabilă a mulțimilor, adică cea mai mare mulțime inclusă în toate mulțimile care trebuie intersectate:

\inf \left\{\,X_{n}:n=1,2,3,\dots \,\right\}={\bigcap _{n=1}^{\infty }}X_{n}

{\ displaystyle \ inf \ left \ {\, X_ {n}: n = 1,2,3, \ dots \, \ right \} = {\ bigcap _ {n = 1} ^ {\ infty}} X_ { n}}

\ inf \ left \ {\, X_n: n = 1,2,3, \ dots \, \ right \} = {\ bigcap_ {n = 1} ^ \ infty} X_n

Succesiunea $\{I_{n}:n\in \mathbb {N} \}$ ${\ displaystyle \ {I_ {n}: n \ in \ mathbb {N} \}}$ $\ {I_n: n \ in \ mathbb {N} \}$ , unde cu $I_{n}$ ${\ displaystyle I_ {n}}$ $În}$ cel mai mic dintre mulțimile cu indice mai mare sau egal cu n este notat, este nedescrescător, deoarece $I_{n}\subset I_{n+1}$ ${\ displaystyle I_ {n} \ subset I_ {n + 1}}$ $I_n \ subset I_ {n + 1}$ . Prin urmare, uniunea celui mai mic raport față de indicii de la 1 la n este egală cu al n-lea cel mai mic. A face ca această succesiune de seturi să ajungă la limită:

\liminf _{n\rightarrow \infty }X_{n}={\bigcup _{n=1}^{\infty }}\left({\bigcap _{m=n}^{\infty }}X_{m}\right)

{\ displaystyle \ liminf _ {n \ rightarrow \ infty} X_ {n} = {\ bigcup _ {n = 1} ^ {\ infty}} \ left ({\ bigcap _ {m = n} ^ {\ infty} } X_ {m} \ dreapta)}

\ liminf_ {n \ rightarrow \ infty} X_n = {\ bigcup_ {n = 1} ^ \ infty} \ left ({\ bigcap_ {m = n} ^ \ infty} X_m \ right)

Limsup-ul poate fi definit simetric. Suprema unei succesiuni de mulțimi este cea mai mică mulțime care conține toate mulțimile, adică uniunea numărabilă a mulțimilor.

\sup \left\{\,X_{n}:n=1,2,3,\dots \,\right\}={\bigcup _{n=1}^{\infty }}X_{n}

{\ displaystyle \ sup \ left \ {\, X_ {n}: n = 1,2,3, \ dots \, \ right \} = {\ bigcup _ {n = 1} ^ {\ infty}} X_ { n}}

\ sup \ left \ {\, X_n: n = 1,2,3, \ dots \, \ right \} = {\ bigcup_ {n = 1} ^ \ infty} X_n

Limsup este în schimb intersecția numărabilă a acestei secvențe care nu crește (fiecare suprem este un subset al supremului care o precedă)

\limsup _{n\rightarrow \infty }X_{n}={\bigcap _{n=1}^{\infty }}\left({\bigcup _{m=n}^{\infty }}X_{m}\right)

{\ displaystyle \ limsup _ {n \ rightarrow \ infty} X_ {n} = {\ bigcap _ {n = 1} ^ {\ infty}} \ left ({\ bigcup _ {m = n} ^ {\ infty} } X_ {m} \ dreapta)}

\ limsup_ {n \ rightarrow \ infty} X_n = {\ bigcap_ {n = 1} ^ \ infty} \ left ({\ bigcup_ {m = n} ^ \ infty} X_m \ right)

Pentru un exemplu, a se vedea lema Borel-Cantelli . Când aceste două seturi coincid, vorbim despre un set limită al secvenței $(X_{n})_{n}$ ${\ displaystyle (X_ {n}) _ {n}}$ $(X_n) _n$ .

Notă

^ W. Rudin , Pagina 13 .
^ ^a ^b W. Rudin , p . 14 .

Bibliografie

Walter Rudin, Analiză reală și complexă , Mladinska Knjiga, McGraw-Hill, 1970, ISBN 0-07-054234-1 .
( EN ) H. Amann, Escher, Joachim, Analysis , Basel; Boston: Birkhäuser, 2005, ISBN 0-8176-7153-6 .
( EN ) Mario O González, Analiza complexă clasică , New York: M. Dekker, 1991, ISBN 0-8247-8415-4 .

Elemente conexe

Alte proiecte

Wikiversitatea conține resurse cu privire la limite
Wikimedia Commons conține imagini sau alte fișiere despre limite

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[def-1] W. Rudin , Pagina 13 .

[conv-2] W. Rudin , p . 14 .

[1]

[2]