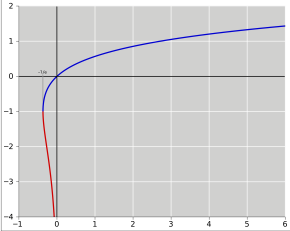
Graficul lui W ( x ) cu W > −4 și x <6. Ramura superioară cu W ≥ −1 este funcția W 0 (ramura principală), ramura inferioară cu W ≤ −1 este funcția W −1 .
În matematică , funcția Lambert W , numită și funcția Omega , este un set de funcții , în mod explicit ramurile funcției inverse ale funcției f ( w ) = w și w , unde e w este funcția exponențială și w este orice număr complex. Cu alte cuvinte, ecuația care definește W ( z ) este
- {\ displaystyle z = W (z) e ^ {W (z)}}

pentru orice număr complex z .
Deoarece funcția ƒ nu este injectivă , funcția W este o funcție polidromat (cu excepția 0). Prin restrângerea atenției la cazul în care W își asumă doar valori reale, atunci relația este definită numai pentru x ≥ −1 / e și se iau două valori distincte în interval (−1 / e , 0); condiția suplimentară W ≥ −1 definește o funcție unică W 0 ( x ). Avem W 0 (0) = 0 și W 0 (−1 / e ) = −1. În același timp, ramura inferioară are W ≤ −1 și este notată cu notația W −1 ( x ). Scade de la W −1 (−1 / e ) = −1 la W −1 (0 - ) = −∞.
Funcția W nu poate fi exprimată în termeni de funcții elementare . Găsește aplicații în combinatorică , de exemplu în enumerarea copacilor . Poate fi utilizat în rezolvarea ecuațiilor care includ funcții exponențiale (de exemplu, maximele distribuțiilor Planck , Bose-Einstein și Fermi-Dirac ) și este, de asemenea, necesar în rezolvarea ecuațiilor diferențiale de tip y ' ( t ) = a y ( t - 1).
Istorie și terminologie
Funcția W poartă numele matematicianului Johann Heinrich Lambert . Lambert a studiat ecuația transcendentă omonimă a lui Lambert în 1758, care a fost urmată de un studiu realizat de Euler în 1783, care a considerat cazul special w și w . Cu toate acestea, funcția inversă a lui w și w a fost descrisă pentru prima dată de Pólya și Szegő în 1925. Funcția W a lui Lambert a fost „redescoperită” aproximativ în fiecare deceniu în aplicații specializate, dar importanța sa nu a fost observată până la sfârșitul anilor '90.
Ramura principală W 0 este indicată cu Wp în Biblioteca digitală a funcțiilor matematice în timp ce ramura W −1 este indicată acolo cu Wm . Notatia folosita in acest articol (cu W 0 si W -1 ) este de acord cu cea folosita de Corless, Gonnet, Hare, Jeffrey si Knuth .
Analize
Derivat
Prin derivare implicită, se poate arăta că toate ramurile lui W satisfac ecuația diferențială
- {\ displaystyle z (1 + W) {\ frac {{\ rm {d}} W} {{\ rm {d}} z}} = W, \ quad z \ neq -1 / e.}

( W nu este diferențiat la z = -1 / e ). Aceasta este o consecință a următoarei formule pentru derivata lui W :
- {\ displaystyle {\ frac {{\ rm {d}} W} {{\ rm {d}} z}} = {\ frac {W (z)} {z (1 + W (z))}}, \ quad z \ not \ in \ {0, -1 / și \}.}

De asemenea, are
- {\ displaystyle \ left. {\ frac {{\ rm {d}} W} {{\ rm {d}} z}} \ right | _ {z = 0} = 1.}

Primitiv
Funcția W ( x ) și multe expresii care includ W ( x ) pot fi integrate prin aplicarea substituției w = W ( x ), adică x = W și W :
- {\ displaystyle \ int W (x) \, {\ rm {d}} x = x \ left (W (x) -1 + {\ frac {1} {W (x)}} \ right) + C. }

| Demonstrație |
|---|
Intr-adevar: - {\ displaystyle \ int W (x) \, {\ rm {d}} x =}

cu înlocuire {\ displaystyle x = We ^ {W}}  {\ displaystyle = \ int W \, {\ rm {d}} (We ^ {W}) = \ int W (e ^ {W} + We ^ {W}) \, {\ rm {d}} W = \ int (W + W ^ {2}) și ^ {W} \, {\ rm {d}} W =}  integrarea pe piese {\ displaystyle = (W + W ^ {2}) e ^ {W} - \ int e ^ {W} (1 + 2W) \, {\ rm {d}} W = (W + W ^ { 2}) e ^ {W} -e ^ {W} -2 \ int We ^ {W} \, {\ rm {d}} W}  În acest moment, integrarea pe părți în ultimul termen: - {\ displaystyle \ int We ^ {W} \, {\ rm {d}} W = We ^ {W} - \ int e ^ {W} \, {\ rm {d}} W = We ^ {W} -e ^ {W} + C}

și înlocuind în expresia anterioară, obținem: - {\ displaystyle \ int W (x) \, {\ rm {d}} x = (W + W ^ {2}) e ^ {W} -e ^ {W} -2We ^ {W} + 2e ^ {W} + C =}

- {\ displaystyle = W ^ {2} e ^ {W} -We ^ {W} + e ^ {W} + C = W \ cdot We ^ {W} -We ^ {W} + {\ frac {We ^ {W}} {W}} + C =}

- {\ displaystyle Wx-x + {\ frac {x} {W}} + C = x \ left (W (x) -1 + {\ frac {1} {W (x)}} \ right) + C}

|
Seria Maclaurin
Seria lui Maclaurin {\ displaystyle W_ {0}}  poate fi găsit folosind teorema de inversiune a lui Lagrange și este dat de
poate fi găsit folosind teorema de inversiune a lui Lagrange și este dat de
- {\ displaystyle W_ {0} (x) = \ sum _ {n = 1} ^ {\ infty} {\ frac {(-n) ^ {n-1}} {n!}} \ x ^ {n} = xx ^ {2} + {\ frac {3} {2}} x ^ {3} - {\ frac {8} {3}} x ^ {4} + {\ frac {125} {24}} x ^ {5} - \ cdots}

Raza de convergență este 1 / e , după cum se poate observa prin aplicarea criteriului rădăcină . Funcția definită de această serie poate fi extinsă la o funcție holomorfă definită pentru orice număr complex. Această funcție definește ramura principală a funcției Lambert W.
Întregi și puteri complexe
Puteri întregi ale {\ displaystyle W_ {0}}  admite o expansiune a seriei Taylor (sau Laurent ) centrată la 0
admite o expansiune a seriei Taylor (sau Laurent ) centrată la 0
- {\ displaystyle W_ {0} (x) ^ {2} = \ sum _ {n = 2} ^ {\ infty} {\ frac {-2 (-n) ^ {n-3}} {(n-2 )!}} \ x ^ {n} = x ^ {2} -2x ^ {3} + 4x ^ {4} - {\ frac {25} {3}} x ^ {5} + 18x ^ {6} - \ cdots}

Mai general, pentru {\ displaystyle r \ in \ mathbb {Z},}  , formula de inversiune Lagrange permite obținerea
, formula de inversiune Lagrange permite obținerea
- {\ displaystyle W_ {0} (x) ^ {r} = \ sum _ {n = r} ^ {\ infty} {\ frac {-r (-n) ^ {nr-1}} {(nr)! }} \ x ^ {n},}

care este, în general, o serie Laurent de ordine r . În mod echivalent, acesta din urmă poate fi scris ca seria lui Taylor {\ displaystyle W_ {0} (x) / x} 
- {\ displaystyle \ left ({\ frac {W_ {0} (x)} {x}} \ right) ^ {r} = e ^ {- rW_ {0} (x)} = \ sum _ {n = 0 } ^ {\ infty} {\ frac {r (n + r) ^ {n-1}} {n!}} \ (-x) ^ {n},}

valabil pentru fiecare {\ displaystyle r \ in \ mathbb {C}}  Și {\ displaystyle | x | <e ^ {- 1}}
Și {\ displaystyle | x | <e ^ {- 1}}  .
.
Valori remarcabile
Pentru orice algebric diferit de zero x W ( x ) este un număr transcendent . Această proprietate poate fi dovedită în mod absurd : dacă W ( x ) ar fi algebric și non-nul (rețineți că dacă x este non-nul, W ( x ) trebuie să fie și el) atunci prin teorema Lindemann-Weierstrass și W ( x ) ar trebui să fie transcendent, ceea ce înseamnă că x = W ( x ) și W ( x ) sunt, de asemenea, transcendenți, contrazicând ipoteza că x este algebric.
- {\ displaystyle W \ left (- {\ frac {\ pi} {2}} \ right) = {\ frac {\ pi} {2}} {\ rm {i}}}

- {\ displaystyle W \ left (-1 \ right) \ approx -0.31813-1.33723 {\ rm {i}}}

- {\ displaystyle W \ left (- {\ frac {1} {e}} \ right) = - 1}

- {\ displaystyle W \ left (0 \ right) = 0}

- {\ displaystyle W \ left (1 \ right) = \ Omega \ approx 0.56714329 \ dots}

- unde este {\ displaystyle \ Omega}
 indică constanta Omega
indică constanta Omega
- {\ displaystyle W \ left (e \ right) = 1}

- {\ displaystyle W (x \ ln x) = \ ln x \ quad \ left ({\ frac {1} {e}} \ leq x \ leq e \ right)}

- {\ displaystyle W '\ left (0 \ right) = 1}

Alte proprietăți integrale
- {\ displaystyle \ int _ {0} ^ {\ pi} W {\ bigl (} 2 \ cot ^ {2} (x) {\ bigr)} \ sec ^ {2} (x) \; \ mathrm {d } x = 4 {\ sqrt {\ pi}}}

- {\ displaystyle \ int _ {0} ^ {+ \ infty} W \ left ({\ frac {1} {x ^ {2}}} \ right) \; \ mathrm {d} x = {\ sqrt {2 \ pi}}}

- {\ displaystyle \ int _ {0} ^ {+ \ infty} {\ frac {W (x)} {x {\ sqrt {x}}}} \ mathrm {d} x = 2 {\ sqrt {2 \ pi }}}

Aplicații
Multe ecuații care includ exponențieri pot fi rezolvate folosind funcția W. Strategia generală este de a muta toate aparițiile necunoscutului către un membru pentru a obține o formă de tip Y = Xe X , moment în care funcția W furnizează valoarea variabilei în X.
Cu alte cuvinte:
- {\ displaystyle Y = Xe ^ {X} \; \ Longleftrightarrow \; X = W (Y)}

Exemplul 1
- {\ displaystyle 2 ^ {t} = 5t}

- {\ displaystyle \ Rightarrow 1 = {\ frac {5t} {2 ^ {t}}}}

- {\ displaystyle \ Rightarrow 1 = 5t \, e ^ {- t \ ln 2}}

- {\ displaystyle \ Rightarrow {\ frac {1} {5}} = t \, e ^ {- t \ ln 2}}

- {\ displaystyle \ Rightarrow {\ frac {- \, \ ln 2} {5}} = (- \, t \, \ ln 2) \, e ^ {(- t \ ln 2)}}

- {\ displaystyle \ Rightarrow W \ left ({\ frac {- \ ln 2} {5}} \ right) = - t \ ln 2}

- {\ displaystyle \ Rightarrow t = - {\ frac {1} {\ ln 2}} W \ left ({\ frac {- \ ln 2} {5}} \ right)}

Mai general, ecuația
- {\ displaystyle ~ p ^ {ax + b} = cx + d}

unde este
- {\ displaystyle p> 0 {\ text {e}} c, a \ neq 0}

poate fi transformat prin substituție
- {\ displaystyle -t = ax + {\ frac {ad} {c}}}

în
- {\ displaystyle tp ^ {t} = R = - {\ frac {a} {c}} p ^ {b - {\ frac {ad} {c}}}}

obtinerea
- {\ displaystyle t = {\ frac {W (R \ ln p)} {\ ln p}}}

care oferă soluția finală
- {\ displaystyle x = - {\ frac {d} {c}} - {\ frac {1} {a \ ln p}} W \ left (- {\ frac {a} {c}} \, p ^ { b - {\ frac {ad} {c}}} \ ln p \ right)}

În mod similar, derivăm că ecuația
- {\ displaystyle p ^ {ax + b} \, (cx + d) = q}

are pentru soluție
- {\ displaystyle x = - {\ frac {d} {c}} + {\ frac {1} {a \ ln p}} W \ left (q \, {\ frac {a} {c}} \, p ^ {{\ frac {ad} {c}} - b} \ ln p \ right)}

Exemplul 2
{\ displaystyle \ ln (x) = 1 + ax \ \}  cu {\ displaystyle \ a \ neq 0}
cu {\ displaystyle \ a \ neq 0} 
- {\ displaystyle \ Rightarrow x = e ^ {1 + ax} = e \ cdot e ^ {ax}}

- {\ displaystyle \ Rightarrow e = x \ cdot e ^ {- ax}}

- {\ displaystyle \ Rightarrow -ae = -ax \ cdot e ^ {- ax}}

- {\ displaystyle \ Rightarrow W (-ae) = - ax}

- {\ displaystyle \ Rightarrow x = - {\ frac {W (-ae)} {a}}}

Mai general, pentru a rezolva ecuația:
- {\ displaystyle \ log _ {p} (ax + b) = cx + d}

unde este
- {\ displaystyle p> 0 \ {\ text {e}} \ neq 1, \ \ a, c \ neq 0,}

există două moduri.
Primul este să ridici {\ displaystyle p}  la fiecare membru al acestei ecuații, revenind astfel la exemplul 1:
la fiecare membru al acestei ecuații, revenind astfel la exemplul 1:
- {\ displaystyle ax + b = p ^ {cx + d}}

Al doilea este după cum urmează:
- {\ displaystyle \ log _ {p} (ax + b) = cx + d}

- {\ displaystyle \ Rightarrow {\ frac {\ ln (ax + b)} {\ ln p}} = cx + d}

- {\ displaystyle \ Rightarrow \ ln (ax + b) = cx \ cdot \ ln p + d \ cdot \ ln p}

- {\ displaystyle \ Rightarrow ax + b = e ^ {cx \ cdot \ ln p + d \ cdot \ ln p} = p ^ {d} \ cdot e ^ {cx \ cdot \ ln p}}

- {\ displaystyle \ Rightarrow p ^ {d} = (ax + b) \ cdot e ^ {- cx \ cdot \ ln p}}

- {\ displaystyle \ Rightarrow - {\ frac {c \ ln p} {a}} \ cdot p ^ {d} = - (cx \ cdot \ ln p + {\ frac {bc \ ln p} {a}}) \ cdot e ^ {- cx \ cdot \ ln p}}

- {\ displaystyle \ Rightarrow - {\ frac {c \ ln p} {a}} \ cdot p ^ {d} \ cdot e ^ {- {\ frac {bc \ ln p} {a}}} = - \ left (cx \ cdot \ ln p + {\ frac {bc \ ln p} {a}} \ right) \ cdot e ^ {- \ left (cx \ cdot \ ln p + {\ frac {bc \ ln p} { a}} \ right)}}

- {\ displaystyle \ Rightarrow - {\ frac {c \ ln p} {a}} \ cdot p ^ {d - {\ frac {bc} {a}}} = - \ left (cx \ cdot \ ln p + { \ frac {bc \ ln p} {a}} \ right) \ cdot e ^ {- \ left (cx \ cdot \ ln p + {\ frac {bc \ ln p} {a}} \ right)}}

- {\ displaystyle \ Rightarrow W \ left (- {\ frac {c \ ln p} {a}} \ cdot p ^ {d - {\ frac {bc} {a}}} \ right) = - \ left (cx \ cdot \ ln p + {\ frac {bc \ ln p} {a}} \ right)}

- {\ displaystyle \ Rightarrow {\ frac {bc \ ln p} {a}} + W \ left (- {\ frac {c \ ln p} {a}} \ cdot p ^ {d - {\ frac {bc} {a}}} \ right) = - cx \ cdot \ ln p}

- {\ displaystyle \ Rightarrow x = - {\ frac {b} {a}} - {\ frac {1} {c \ ln p}} W \ left (- {\ frac {c} {a}} p ^ { d - {\ frac {bc} {a}}} \ ln p \ right)}

Exemplul 3
- {\ displaystyle a ^ {x} = bx ^ {c} \ \ \}
 cu {\ displaystyle a> 0 \ {\ text {e}} \ neq 1, \ \ b, c \ neq 0}
cu {\ displaystyle a> 0 \ {\ text {e}} \ neq 1, \ \ b, c \ neq 0} 
- {\ displaystyle \ Rightarrow a ^ {x / c} = b ^ {1 / c} \ x}

- {\ displaystyle \ Rightarrow 1 = {\ frac {b ^ {1 / c} \ x} {a ^ {x / c}}}}

- {\ displaystyle \ Rightarrow 1 = b ^ {1 / c} \ x \ e ^ {- (x / c) \ ln (a)}}

- {\ displaystyle \ Rightarrow {\ frac {1} {b ^ {1 / c}}} = x \ e ^ {- (x / c) \ ln (a)}}

- {\ displaystyle \ Rightarrow - {\ frac {\ ln (a)} {c \ b ^ {1 / c}}} = - (x / c) \ ln (a) \ e ^ {- (x / c) \ ln (a)}}

- {\ displaystyle \ Rightarrow W \ left (- {\ frac {\ ln (a)} {c \ b ^ {1 / c}}} \ right) = - (x / c) \ ln (a)}

- {\ displaystyle \ Rightarrow x = - {\ frac {c} {\ ln (a)}} W \ left (- {\ frac {\ ln (a)} {c \ b ^ {1 / c}}} \ dreapta)}

Exemplul 4
Ecuația
- {\ displaystyle x ^ {x} = z \ ,,}

poate fi rezolvat cu două tehnici diferite:
- {\ displaystyle \ Rightarrow x \ ln x = \ ln z}

- {\ displaystyle \ Rightarrow \ ln x \, e ^ {\ ln x} = \ ln z}

- {\ displaystyle \ Rightarrow \ ln x = W (\ ln z)}

- {\ displaystyle \ Rightarrow x = e ^ {W (\ ln z)}}

sau, echivalent,
- {\ displaystyle \ Rightarrow x = z ^ {\ frac {1} {x}}}

- {\ displaystyle \ Rightarrow 1 = {\ frac {1} {x}} e ^ {\ frac {\ ln z} {x}}}

- {\ displaystyle \ Rightarrow \ ln z = {\ frac {\ ln z} {x}} e ^ {\ frac {\ ln z} {x}}}

- {\ displaystyle \ Rightarrow W (\ ln z) = {\ frac {\ ln z} {x}}}

- {\ displaystyle \ Rightarrow x = {\ frac {\ ln z} {W (\ ln z)}}}

Rețineți că cele două forme sunt echivalente prin aceea că însăși definiția lui W
- {\ displaystyle e ^ {W (x)} = {\ frac {x} {W (x)}}.}

Exemplul 5
Tetrarea infinită
- {\ displaystyle x ^ {x ^ {x ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}} \ \,}

după cum a demonstrat Euler în 1783, [1] converge pentru e - e ≤ x ≤ e 1 / e ; după cum a demonstrat Eisenstein în 1844, [2] funcția W oferă valoarea limită:
- {\ displaystyle \ ell = {\ frac {W (- \ ln x)} {- \ ln x}} = e ^ {- W (- \ ln x)}.}

Generalizări
Funcția W a lui Lambert oferă soluții reale pentru ecuațiile algebric-transcendente (în x ) ale formei:
- {\ displaystyle e ^ {- cx} = a_ {o} (xr) ~~ \ quad \ qquad \ qquad \ qquad \ qquad (1)}

unde a 0 , c și r sunt constante reale. Soluția este {\ displaystyle x = r + W (ce ^ {- cr} / a_ {o}) / c}  . Generalizările funcției Lambert W [3] [4] [5] includ:
. Generalizările funcției Lambert W [3] [4] [5] includ:
- {\ displaystyle e ^ {- cx} = a_ {o} (x-r_ {1}) (x-r_ {2}) ~~ \ qquad \ qquad (2)}

- unde partea dreaptă a lui (1) este un polinom pătratic în x , iar r 1 și r 2 sunt constante reale distincte, rădăcinile polinomului pătratic. În acest caz, soluția este o singură funcție argument x, iar termenii r i și o sunt parametrii acestei funcții. Din acest punct de vedere, generalizarea seamănă cu funcția hipergeometrică și funcția Meijer G, dar aparține unei clase diferite de funcții. Când r 1 = r 2 , ambele părți ale lui (2) pot fi luate în considerare și reduse la cazul (1); deci soluția este cea a funcției standard W. Ecuația (2) descrie câmpul dilaton , din care derivă metrica problemei gravitației cu doi corpuri R = T sau liniară în dimensiuni 1 + 1 (o dimensiune spațială și o dimensiune temporală) pentru cazul maselor în repaus diferite, ca precum și energiile din modelul cuantic unidimensional al unui puț dublu potențial, cu potențiale delta Dirac, pentru sarcini diferite.
- Soluții analitice ale energiilor unui caz particular al problemei cuantice a celor trei corpuri, mai exact molecula de hidrogen odată ionizată [7] . În acest caz, partea dreaptă a lui (1) (sau (2)) este un coeficient de polinoame în x de grad infinit:
- {\ displaystyle e ^ {- cx} = a_ {o} {\ frac {\ prod _ {i = 1} ^ {\ infty} (x-r_ {i})} {\ prod _ {i = 1} ^ {\ infty} (x-s_ {i})}} \ qquad \ qquad \ qquad (3)}

- unde r i și s i sunt constante reale distincte și x este o funcție de energie și R. distanța internuclear Ecuația (3), cu cazurile speciale (1) și (2), joacă un rol într-o clasă mare de ecuații diferențiale întârziate. Datorită noțiunii lui Hardy de „derivată falsă”, s-au găsit mai multe rădăcini exacte pentru cazuri speciale de ecuații (3) [8] .
Aplicațiile funcției W a lui Lambert la problemele fundamentale de fizică nu sunt epuizate nici măcar pentru cazul standard (1), așa cum sa văzut recent în fizica atomică, moleculară și optică [9] .
Valorile numerice
Funcția W poate fi aproximată folosind metoda tangentă , cu aproximarea succesivă a {\ displaystyle w = W (z)}  (astfel încât {\ displaystyle z = we ^ {w}}
(astfel încât {\ displaystyle z = we ^ {w}}  ) prin
) prin
- {\ displaystyle w_ {j + 1} = w_ {j} - {\ frac {w_ {j} e ^ {w_ {j}} - z} {e ^ {w_ {j}} + w_ {j} e ^ {w_ {j}}}}.}

Funcția W poate fi, de asemenea, aproximată folosind metoda lui Halley,
- {\ displaystyle w_ {j + 1} = w_ {j} - {\ frac {w_ {j} e ^ {w_ {j}} - z} {e ^ {w_ {j}} (w_ {j} +1 ) - {\ frac {(w_ {j} +2) (w_ {j} e ^ {w_ {j}} - z)} {2w_ {j} +2}}}}.}

Grafice
- Grafice ale funcției Lambert W în planul complex
Notă
- ^ Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2 , 29–51, 1783. Reeditat în Euler, L. Opera Omnia, Seria Prima, Vol. 6: Commentationes Algebraicae . Leipzig, Germania: Teubner, pp. 350–369, 1921. ( facsimil )
- ^ Funcția W (x) , pe bitman.name . Adus la 20 iulie 2020 .
- ^ TC Scott și RB Mann, General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function , AAECC (Aplicable Algebra in Engineering, Communication and Computing), vol. 17, nr. 1, (aprilie 2006), pp. 41-47, [1] ; articol Arxiv [2]
- ^ TC Scott, G. Fee și J. Grotendorst, „Seria asimptotică a funcției Lambert W generalizate” , SIGSAM, vol. 47, nr. 3, (septembrie 2013), pp. 75-83
- ^ TC Scott, G. Fee, J. Grotendorst și WZ Zhang, "Numerica funcției generalizate Lambert W" , SIGSAM, vol. 48, nr. 2, (iunie 2014), pp. 42-56
- ^ PS Farrugia, RB Mann și TC Scott, N-body Gravity și ecuația Schrˆdinger , clasa. Quantum Grav. vol. 24, (2007), pp. 4647-4659, [3] ; articol Arxiv [4]
- ^ TC Scott, M. Aubert-Frécon și J. Grotendorst, Noua abordare pentru energiile electronice ale ionului molecular de hidrogen , Chem. Fizic. vol. 324, (2006), pp. 323-338, [5] Arhivat la 31 martie 2009 la Internet Archive ; articol Arxiv [6]
- ^ Aude Maignan și TC Scott, "Fleshing out the Generalized Lambert W Function", SIGSAM, vol. 50, nr. 2, (iunie 2016), pp. 45-60
- ^ TC Scott, A. Lüchow, D. Bressanini și JD Morgan III, Suprafețele nodale ale funcțiilor proprii ale atomului de heliu , Phys. Rev. A 75, (2007), p. 060101, [7]
Elemente conexe
Alte proiecte
linkuri externe
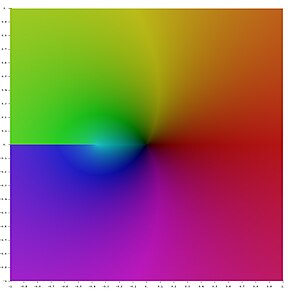 Ramura principală a funcției W în planul complex. Hue reprezintă argumentul funcției, în timp ce intensitatea reprezintă modulul .
Ramura principală a funcției W în planul complex. Hue reprezintă argumentul funcției, în timp ce intensitatea reprezintă modulul . Wikimedia Commons conține imagini sau alte fișiere despre Funcția W a lui Lambert
Wikimedia Commons conține imagini sau alte fișiere despre Funcția W a lui Lambert


























































































































