Funcția zeta Hurwitz

În matematică , în special în teoria numerelor analitice , funcția zeta Hurwitz este o funcție zeta care își datorează numele matematicianului german Adolf Hurwitz . Funcția este definită prin serie

\zeta (s,q)=\sum _{n=0}^{\infty }{\frac {1}{(q+n)^{s}}},

{\ displaystyle \ zeta (s, q) = \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {(q + n) ^ {s}}},}

{\ displaystyle \ zeta (s, q) = \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {(q + n) ^ {s}}},}

de sine $\operatorname {Re} (s)>1$ ${\ displaystyle \ operatorname {Re} (s)> 1}$ ${\ displaystyle \ operatorname {Re} (s)> 1}$ Și $\operatorname {Re} (q)>0$ ${\ displaystyle \ operatorname {Re} (q)> 0}$ ${\ displaystyle \ operatorname {Re} (q)> 0}$ . În mod evident, dacă $q=1$ ${\ displaystyle q = 1}$ $q = 1$ funcția Hurwitz zeta coincide cu funcția zeta Riemann , adică $\zeta (s,1)=\zeta (s)$ ${\ displaystyle \ zeta (s, 1) = \ zeta (s)}$ ${\ displaystyle \ zeta (s, 1) = \ zeta (s)}$ .

La fel ca funcția zeta Riemann, $\zeta (s,q)$ ${\ displaystyle \ zeta (s, q)}$ ${\ displaystyle \ zeta (s, q)}$ poate fi extins analitic la o funcție holomorfă pe întregul plan complex , cu excepția $s=1$ ${\ displaystyle s = 1}$ $s = 1$ .

Funcția zeta Hurwitz cu

q=1/3

{\ displaystyle q = 1/3}

{\ displaystyle q = 1/3}

. Complotul a fost realizat cu matplotlib folosind o versiune a metodei de colorare a domeniului . ^[1]

Extensie analitică

Funcția zeta Hurwitz cu

q=24/25

{\ displaystyle q = 24/25}

{\ displaystyle q = 24/25}

.

De sine $\mathrm {Re} (s)\leq 1$ ${\ displaystyle \ mathrm {Re} (s) \ leq 1}$ ${\ displaystyle \ mathrm {Re} (s) \ leq 1}$ , funcția poate fi definită prin intermediul următoarei ecuații

\zeta (s,q)=\Gamma (1-s){\frac {1}{2\pi i}}\int _{C}{\frac {z^{s-1}e^{qz}}{1-e^{z}}}dz

{\ displaystyle \ zeta (s, q) = \ Gamma (1-s) {\ frac {1} {2 \ pi i}} \ int _ {C} {\ frac {z ^ {s-1} e ^ {qz}} {1-e ^ {z}}} dz}

{\ displaystyle \ zeta (s, q) = \ Gamma (1-s) {\ frac {1} {2 \ pi i}} \ int _ {C} {\ frac {z ^ {s-1} e ^ {qz}} {1-e ^ {z}}} dz}

unde conturul $C.$ ${\ displaystyle C}$ $C.$ este o linie închisă în jurul axei reale negative.

Putem apoi să ne prelungim analitic până la o funcție meromorfă , cu punctul $s=1$ ${\ displaystyle s = 1}$ $s = 1$ ca un singur pol simplu și rezidual $1$ ${\ displaystyle 1}$ $1$ . Termenul constant este dat de

\lim _{s\to 1}\left[\zeta (s,q)-{\frac {1}{s-1}}\right]={\frac {-\Gamma '(q)}{\Gamma (q)}}=-\psi (q)

{\ displaystyle \ lim _ {s \ to 1} \ left [\ zeta (s, q) - {\ frac {1} {s-1}} \ right] = {\ frac {- \ Gamma '(q) } {\ Gamma (q)}} = - \ psi (q)}

{\ displaystyle \ lim _ {s \ to 1} \ left [\ zeta (s, q) - {\ frac {1} {s-1}} \ right] = {\ frac {- \ Gamma '(q) } {\ Gamma (q)}} = - \ psi (q)}

unde este $\Gamma$ ${\ displaystyle \ Gamma}$ $\Gamă$ este funcția Gamma și $\psi$ ${\ displaystyle \ psi}$ $\ psi$ funcția digamă .

Reprezentări

Reprezentare în serie

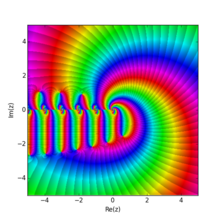
Funcția zeta Hurwitz cu parametru

q

{\ displaystyle q}

q

Și

s=3+4i

{\ displaystyle s = 3 + 4i}

{\ displaystyle s = 3 + 4i}

.

În 1930, Helmut Hasse ^{[2] a} furnizat o reprezentare convergentă a seriei Newton definită pentru $q>0$ ${\ displaystyle q> 0}$ ${\ displaystyle q> 0}$ real și $s\neq 1$ ${\ displaystyle s \ neq 1}$ ${\ displaystyle s \ neq 1}$ :

\zeta (s,q)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(q+k)^{1-s}.

{\ displaystyle \ zeta (s, q) = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {n + 1}} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {n \ alege k} (q + k) ^ {1-s}.}

{\ displaystyle \ zeta (s, q) = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {n + 1}} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {n \ alege k} (q + k) ^ {1-s}.}

Această serie converge uniform în fiecare subset compact al jumătății planului $s$ ${\ displaystyle s}$ $s$ la o funcție întreagă . Se înțelege că suma internă este $n$ ${\ displaystyle n}$ $n$ -a diferență înainte de $q^{1-s}$ ${\ displaystyle q ^ {1-s}}$ ${\ displaystyle q ^ {1-s}}$ , acesta este

\Delta ^{n}q^{1-s}=\sum _{k=0}^{n}(-1)^{n-k}{n \choose k}(q+k)^{1-s}

{\ displaystyle \ Delta ^ {n} q ^ {1-s} = \ sum _ {k = 0} ^ {n} (- 1) ^ {nk} {n \ alege k} (q + k) ^ { 1-s}}

{\ displaystyle \ Delta ^ {n} q ^ {1-s} = \ sum _ {k = 0} ^ {n} (- 1) ^ {nk} {n \ alege k} (q + k) ^ { 1-s}}

unde este $\Delta$ ${\ displaystyle \ Delta}$ $\ Delta$ este operatorul diferenței directe. Deci, puteți scrie

{\begin{aligned}\zeta (s,q)&={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n+1}}\Delta ^{n}q^{1-s}\\&={\frac {1}{s-1}}{\log(1+\Delta ) \over \Delta }q^{1-s}\end{aligned}}

{\ displaystyle {\ begin {align} \ zeta (s, q) & = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1 ) ^ {n}} {n + 1}} \ Delta ^ {n} q ^ {1-s} \\ & = {\ frac {1} {s-1}} {\ log (1+ \ Delta) \ over \ Delta} q ^ {1-s} \ end {align}}}

{\ displaystyle {\ begin {align} \ zeta (s, q) & = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1 ) ^ {n}} {n + 1}} \ Delta ^ {n} q ^ {1-s} \\ & = {\ frac {1} {s-1}} {\ log (1+ \ Delta) \ over \ Delta} q ^ {1-s} \ end {align}}}

Alte serii convergente la nivel global sunt următoarele

\zeta (s,v-1)={\frac {1}{s-1}}\sum _{n=0}^{\infty }H_{n+1}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{1-s}

{\ displaystyle \ zeta (s, v-1) = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} H_ {n + 1} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {1-s}}

{\ displaystyle \ zeta (s, v-1) = {\ frac {1} {s-1}} \ sum _ {n = 0} ^ {\ infty} H_ {n + 1} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {1-s}}

\zeta (s,v)={\frac {k!}{(s-k)_{k}}}\sum _{n=0}^{\infty }{\frac {1}{(n+k)!}}\left[{n+k \atop n}\right]\sum _{l=0}^{n+k-1}\!(-1)^{l}{\binom {n+k-1}{l}}(l+v)^{k-s},\quad k=1,2,3,\ldots

{\ displaystyle \ zeta (s, v) = {\ frac {k!} {(sk) _ {k}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {(n + k)!}} \ left [{n + k \ atop n} \ right] \ sum _ {l = 0} ^ {n + k-1} \! (- 1) ^ {l} {\ binom { n + k-1} {l}} (l + v) ^ {ks}, \ quad k = 1,2,3, \ ldots}

{\ displaystyle \ zeta (s, v) = {\ frac {k!} {(sk) _ {k}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {(n + k)!}} \ left [{n + k \ atop n} \ right] \ sum _ {l = 0} ^ {n + k-1} \! (- 1) ^ {l} {\ binom { n + k-1} {l}} (l + v) ^ {ks}, \ quad k = 1,2,3, \ ldots}

\zeta (s,v)={\frac {v^{1-s}}{s-1}}+\sum _{n=0}^{\infty }|G_{n+1}|\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}

{\ displaystyle \ zeta (s, v) = {\ frac {v ^ {1-s}} {s-1}} + \ sum _ {n = 0} ^ {\ infty} | G_ {n + 1} | \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

{\ displaystyle \ zeta (s, v) = {\ frac {v ^ {1-s}} {s-1}} + \ sum _ {n = 0} ^ {\ infty} | G_ {n + 1} | \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

\zeta (s,v)={\frac {(v-1)^{1-s}}{s-1}}-\sum _{n=0}^{\infty }C_{n+1}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}

{\ displaystyle \ zeta (s, v) = {\ frac {(v-1) ^ {1-s}} {s-1}} - \ sum _ {n = 0} ^ {\ infty} C_ {n +1} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

{\ displaystyle \ zeta (s, v) = {\ frac {(v-1) ^ {1-s}} {s-1}} - \ sum _ {n = 0} ^ {\ infty} C_ {n +1} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

\zeta (s,v){\big (}v-{\tfrac {1}{2}}{\big )}={\frac {s-2}{s-1}}\zeta (s-1,v)+\sum _{n=0}^{\infty }(-1)^{n}G_{n+2}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}

{\ displaystyle \ zeta (s, v) {\ big (} v - {\ tfrac {1} {2}} {\ big)} = {\ frac {s-2} {s-1}} \ zeta ( s-1, v) + \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} G_ {n + 2} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

{\ displaystyle \ zeta (s, v) {\ big (} v - {\ tfrac {1} {2}} {\ big)} = {\ frac {s-2} {s-1}} \ zeta ( s-1, v) + \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} G_ {n + 2} \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

\zeta (s,v)=-\sum _{l=1}^{k-1}{\frac {(k-l+1)_{l}}{(s-l)_{l}}}\zeta (s-l,v)+\sum _{l=1}^{k}{\frac {(k-l+1)_{l}}{(s-l)_{l}}}v^{l-s}+k\sum _{n=0}^{\infty }(-1)^{n}G_{n+1}^{(k)}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}

{\ displaystyle \ zeta (s, v) = - \ sum _ {l = 1} ^ {k-1} {\ frac {(k-l + 1) _ {l}} {(sl) _ {l}}} \ zeta (sl, v) + \ sum _ {l = 1} ^ {k} {\ frac {(kl + 1) _ {l}} {(sl) _ {l}}} v ^ {ls} + k \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} G_ {n + 1} ^ {(k)} \ sum _ {k = 0} ^ {n} (-1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

{\ displaystyle \ zeta (s, v) = - \ sum _ {l = 1} ^ {k-1} {\ frac {(k-l + 1) _ {l}} {(sl) _ {l}}} \ zeta (sl, v) + \ sum _ {l = 1} ^ {k} {\ frac {(kl + 1) _ {l}} {(sl) _ {l}}} v ^ {ls} + k \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} G_ {n + 1} ^ {(k)} \ sum _ {k = 0} ^ {n} (-1) ^ {k} {\ binom {n} {k}} (k + v) ^ {- s}}

unde este $H_{n}$ ${\ displaystyle H_ {n}}$ $H_ {n}$ sunt numerele armonice , $\left[{\cdot \atop \cdot }\right]$ ${\ displaystyle \ left [{\ cdot \ atop \ cdot} \ right]}$ ${\ displaystyle \ left [{\ cdot \ atop \ cdot} \ right]}$ sunt numerele Stirling de primul fel, $(\ldots )_{\ldots }$ ${\ displaystyle (\ ldots) _ {\ ldots}}$ ${\ displaystyle (\ ldots) _ {\ ldots}}$ este simbolul lui Pochhammer , $G_{n}$ ${\ displaystyle G_ {n}}$ $G_ {n}$ sunt coeficienții lui Gregory, $G_{n}^{(k)}$ ${\ displaystyle G_ {n} ^ {(k)}}$ ${\ displaystyle G_ {n} ^ {(k)}}$ sunt coeficienții Gregory de ordin superior și $C_{n}$ ${\ displaystyle C_ {n}}$ $C_n$ sunt numerele Cauchy de al doilea tip ( $C_{1}=1/2$ ${\ displaystyle C_ {1} = 1/2}$ ${\ displaystyle C_ {1} = 1/2}$ , $C_{2}=5/12$ ${\ displaystyle C_ {2} = 5/12}$ ${\ displaystyle C_ {2} = 5/12}$ , $C_{3}=3/8$ ${\ displaystyle C_ {3} = 3/8}$ ${\ displaystyle C_ {3} = 3/8}$ , ...), vezi articolul lui Blagouchine ^[3] .

Reprezentare integrală

Funcția are o reprezentare integrală în termenul transformatei Mellin ,

\zeta (s,q)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {t^{s-1}e^{-qt}}{1-e^{-t}}}dt

{\ displaystyle \ zeta (s, q) = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ infty} {\ frac {t ^ {s-1} e ^ { -qt}} {1-e ^ {- t}}} dt}

{\ displaystyle \ zeta (s, q) = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ infty} {\ frac {t ^ {s-1} e ^ { -qt}} {1-e ^ {- t}}} dt}

pentru $\mathrm {Re} (s)>1$ ${\ displaystyle \ mathrm {Re} (s)> 1}$ ${\ displaystyle \ mathrm {Re} (s)> 1}$ Și $\mathrm {Re} (q)>0.$ ${\ displaystyle \ mathrm {Re} (q)> 0.}$ ${\ displaystyle \ mathrm {Re} (q)> 0.}$

Proprietate

Formula Hurwitz

Formula lui Hurwitz afirmă că

\zeta (1-s,x)={\frac {1}{2s}}\left[e^{-i\pi s/2}\beta (x;s)+e^{i\pi s/2}\beta (1-x;s)\right]

{\ displaystyle \ zeta (1-s, x) = {\ frac {1} {2s}} \ left [e ^ {- i \ pi s / 2} \ beta (x; s) + e ^ {i \ pi s / 2} \ beta (1-x; s) \ dreapta]}

{\ displaystyle \ zeta (1-s, x) = {\ frac {1} {2s}} \ left [e ^ {- i \ pi s / 2} \ beta (x; s) + e ^ {i \ pi s / 2} \ beta (1-x; s) \ dreapta]}

unde este

\beta (x;s)=2\Gamma (s+1)\sum _{n=1}^{\infty }{\frac {\exp(2\pi inx)}{(2\pi n)^{s}}}={\frac {2\Gamma (s+1)}{(2\pi )^{s}}}{\mbox{Li}}_{s}(e^{2\pi ix})

{\ displaystyle \ beta (x; s) = 2 \ Gamma (s + 1) \ sum _ {n = 1} ^ {\ infty} {\ frac {\ exp (2 \ pi inx)} {(2 \ pi n) ^ {s}}} = {\ frac {2 \ Gamma (s + 1)} {(2 \ pi) ^ {s}}} {\ mbox {Li}} _ {s} (e ^ {2 \ pi ix})}

{\ displaystyle \ beta (x; s) = 2 \ Gamma (s + 1) \ sum _ {n = 1} ^ {\ infty} {\ frac {\ exp (2 \ pi inx)} {(2 \ pi n) ^ {s}}} = {\ frac {2 \ Gamma (s + 1)} {(2 \ pi) ^ {s}}} {\ mbox {Li}} _ {s} (e ^ {2 \ pi ix})}

este reprezentarea funcției valabilă pentru $0\leq x\leq 1$ ${\ displaystyle 0 \ leq x \ leq 1}$ ${\ displaystyle 0 \ leq x \ leq 1}$ Și $s>1$ ${\ displaystyle s> 1}$ ${\ displaystyle s> 1}$ , și apoi ${\text{Li}}_{s}(z)$ ${\ displaystyle {\ text {Li}} _ {s} (z)}$ ${\ displaystyle {\ text {Li}} _ {s} (z)}$ indică polilogaritmul .

Ecuația funcțională

Ecuația funcțională raportează valorile funcției Hurwitz din partea dreaptă și stângă a planului complex. Pentru $1\leq m\leq n$ ${\ displaystyle 1 \ leq m \ leq n}$ ${\ displaystyle 1 \ leq m \ leq n}$ numere întregi, pentru orice valoare de $s$ ${\ displaystyle s}$ $s$ da ai

\zeta \left(1-s,{\frac {m}{n}}\right)={\frac {2\Gamma (s)}{(2\pi n)^{s}}}\sum _{k=1}^{n}\left[\cos \left({\frac {\pi s}{2}}-{\frac {2\pi km}{n}}\right)\;\zeta \left(s,{\frac {k}{n}}\right)\right].

{\ displaystyle \ zeta \ left (1-s, {\ frac {m} {n}} \ right) = {\ frac {2 \ Gamma (s)} {(2 \ pi n) ^ {s}}} \ sum _ {k = 1} ^ {n} \ left [\ cos \ left ({\ frac {\ pi s} {2}} - {\ frac {2 \ pi km} {n}} \ right) \ ; \ zeta \ left (s, {\ frac {k} {n}} \ right) \ right].}

{\ displaystyle \ zeta \ left (1-s, {\ frac {m} {n}} \ right) = {\ frac {2 \ Gamma (s)} {(2 \ pi n) ^ {s}}} \ sum _ {k = 1} ^ {n} \ left [\ cos \ left ({\ frac {\ pi s} {2}} - {\ frac {2 \ pi km} {n}} \ right) \ ; \ zeta \ left (s, {\ frac {k} {n}} \ right) \ right].}

Câteva sume finite

Următoarele sume finite sunt strâns legate de ecuația funcțională, dintre care unele pot fi evaluate în formă închisă

\sum _{r=1}^{m-1}\zeta \left(s,{\frac {r}{m}}\right)\cos {\dfrac {2\pi rk}{m}}={\frac {m\Gamma (1-s)}{(2\pi m)^{1-s}}}\sin {\frac {\pi s}{2}}\cdot \left\{\zeta \left(1-s,{\frac {k}{m}}\right)+\zeta \left(1-s,1-{\frac {k}{m}}\right)\right\}-\zeta (s)

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta \ left (s, {\ frac {r} {m}} \ right) \ cos {\ dfrac {2 \ pi rk} {m }} = {\ frac {m \ Gamma (1-s)} {(2 \ pi m) ^ {1-s}}} \ sin {\ frac {\ pi s} {2}} \ cdot \ left \ {\ zeta \ left (1-s, {\ frac {k} {m}} \ right) + \ zeta \ left (1-s, 1 - {\ frac {k} {m}} \ right) \ right \} - \ zeta (s)}

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta \ left (s, {\ frac {r} {m}} \ right) \ cos {\ dfrac {2 \ pi rk} {m }} = {\ frac {m \ Gamma (1-s)} {(2 \ pi m) ^ {1-s}}} \ sin {\ frac {\ pi s} {2}} \ cdot \ left \ {\ zeta \ left (1-s, {\ frac {k} {m}} \ right) + \ zeta \ left (1-s, 1 - {\ frac {k} {m}} \ right) \ right \} - \ zeta (s)}

\sum _{r=1}^{m-1}\zeta \left(s,{\frac {r}{m}}\right)\sin {\dfrac {2\pi rk}{m}}={\frac {m\Gamma (1-s)}{(2\pi m)^{1-s}}}\cos {\frac {\pi s}{2}}\cdot \left\{\zeta \left(1-s,{\frac {k}{m}}\right)-\zeta \left(1-s,1-{\frac {k}{m}}\right)\right\}

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta \ left (s, {\ frac {r} {m}} \ right) \ sin {\ dfrac {2 \ pi rk} {m }} = {\ frac {m \ Gamma (1-s)} {(2 \ pi m) ^ {1-s}}} \ cos {\ frac {\ pi s} {2}} \ cdot \ left \ {\ zeta \ left (1-s, {\ frac {k} {m}} \ right) - \ zeta \ left (1-s, 1 - {\ frac {k} {m}} \ right) \ right \}}

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta \ left (s, {\ frac {r} {m}} \ right) \ sin {\ dfrac {2 \ pi rk} {m }} = {\ frac {m \ Gamma (1-s)} {(2 \ pi m) ^ {1-s}}} \ cos {\ frac {\ pi s} {2}} \ cdot \ left \ {\ zeta \ left (1-s, {\ frac {k} {m}} \ right) - \ zeta \ left (1-s, 1 - {\ frac {k} {m}} \ right) \ right \}}

\sum _{r=1}^{m-1}\zeta ^{2}\left(s,{\frac {r}{m}}\right)={\big (}m^{2s-1}-1{\big )}\zeta ^{2}(s)+{\frac {2m\Gamma ^{2}(1-s)}{(2\pi m)^{2-2s}}}\sum _{l=1}^{m-1}\left\{\zeta \left(1-s,{\frac {l}{m}}\right)-\cos \pi s\cdot \zeta \left(1-s,1-{\frac {l}{m}}\right)\right\}\zeta \left(1-s,{\frac {l}{m}}\right)

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta ^ {2} \ left (s, {\ frac {r} {m}} \ right) = {\ big (} m ^ { 2s-1} -1 {\ big)} \ zeta ^ {2} (s) + {\ frac {2m \ Gamma ^ {2} (1-s)} {(2 \ pi m) ^ {2-2s }}} \ sum _ {l = 1} ^ {m-1} \ left \ {\ zeta \ left (1-s, {\ frac {l} {m}} \ right) - \ cos \ pi s \ cdot \ zeta \ left (1-s, 1 - {\ frac {l} {m}} \ right) \ right \} \ zeta \ left (1-s, {\ frac {l} {m}} \ right )}}

{\ displaystyle \ sum _ {r = 1} ^ {m-1} \ zeta ^ {2} \ left (s, {\ frac {r} {m}} \ right) = {\ big (} m ^ { 2s-1} -1 {\ big)} \ zeta ^ {2} (s) + {\ frac {2m \ Gamma ^ {2} (1-s)} {(2 \ pi m) ^ {2-2s }}} \ sum _ {l = 1} ^ {m-1} \ left \ {\ zeta \ left (1-s, {\ frac {l} {m}} \ right) - \ cos \ pi s \ cdot \ zeta \ left (1-s, 1 - {\ frac {l} {m}} \ right) \ right \} \ zeta \ left (1-s, {\ frac {l} {m}} \ right )}}

unde este $m$ ${\ displaystyle m}$ $m$ este un întreg pozitiv mai mare decât $2$ ${\ displaystyle 2}$ $2$ Și $s$ ${\ displaystyle s}$ $s$ este un număr complex . ^[4] .

Transformată Fourier

Transformata Fourier discretă a funcției zeta Hurwitz în raport cu ordinea $s$ ${\ displaystyle s}$ $s$ este funcția chi a lui Legendre.

Valorile raționale

Funcția zeta Hurwitz calculată în numere raționale apare în multe identități impresionante. ^[5] În special, în ceea ce privește polinoamele lui Euler $E_{n}(x)$ ${\ displaystyle E_ {n} (x)}$ ${\ displaystyle E_ {n} (x)}$ :

E_{2n-1}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n-1)!}{(2\pi q)^{2n}}}\sum _{k=1}^{q}\zeta \left(2n,{\frac {2k-1}{2q}}\right)\cos {\frac {(2k-1)\pi p}{q}}

{\ displaystyle E_ {2n-1} \ left ({\ frac {p} {q}} \ right) = (- 1) ^ {n} {\ frac {4 (2n-1)!} {(2 \ pi q) ^ {2n}}} \ sum _ {k = 1} ^ {q} \ zeta \ left (2n, {\ frac {2k-1} {2q}} \ right) \ cos {\ frac {( 2k-1) \ pi p} {q}}}

{\ displaystyle E_ {2n-1} \ left ({\ frac {p} {q}} \ right) = (- 1) ^ {n} {\ frac {4 (2n-1)!} {(2 \ pi q) ^ {2n}}} \ sum _ {k = 1} ^ {q} \ zeta \ left (2n, {\ frac {2k-1} {2q}} \ right) \ cos {\ frac {( 2k-1) \ pi p} {q}}}

Și

E_{2n}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n)!}{(2\pi q)^{2n+1}}}\sum _{k=1}^{q}\zeta \left(2n+1,{\frac {2k-1}{2q}}\right)\sin {\frac {(2k-1)\pi p}{q}}

{\ displaystyle E_ {2n} \ left ({\ frac {p} {q}} \ right) = (- 1) ^ {n} {\ frac {4 (2n)!} {(2 \ pi q) ^ {2n + 1}}} \ sum _ {k = 1} ^ {q} \ zeta \ left (2n + 1, {\ frac {2k-1} {2q}} \ right) \ sin {\ frac {( 2k-1) \ pi p} {q}}}

{\ displaystyle E_ {2n} \ left ({\ frac {p} {q}} \ right) = (- 1) ^ {n} {\ frac {4 (2n)!} {(2 \ pi q) ^ {2n + 1}}} \ sum _ {k = 1} ^ {q} \ zeta \ left (2n + 1, {\ frac {2k-1} {2q}} \ right) \ sin {\ frac {( 2k-1) \ pi p} {q}}}

În plus,

\zeta \left(s,{\frac {2p-1}{2q}}\right)=2(2q)^{s-1}\sum _{k=1}^{q}\left[C_{s}\left({\frac {k}{q}}\right)\cos \left({\frac {(2p-1)\pi k}{q}}\right)+S_{s}\left({\frac {k}{q}}\right)\sin \left({\frac {(2p-1)\pi k}{q}}\right)\right]

{\ displaystyle \ zeta \ left (s, {\ frac {2p-1} {2q}} \ right) = 2 (2q) ^ {s-1} \ sum _ {k = 1} ^ {q} \ left [C_ {s} \ left ({\ frac {k} {q}} \ right) \ cos \ left ({\ frac {(2p-1) \ pi k} {q}} \ right) + S_ {s } \ left ({\ frac {k} {q}} \ right) \ sin \ left ({\ frac {(2p-1) \ pi k} {q}} \ right) \ right]}

{\ displaystyle \ zeta \ left (s, {\ frac {2p-1} {2q}} \ right) = 2 (2q) ^ {s-1} \ sum _ {k = 1} ^ {q} \ left [C_ {s} \ left ({\ frac {k} {q}} \ right) \ cos \ left ({\ frac {(2p-1) \ pi k} {q}} \ right) + S_ {s } \ left ({\ frac {k} {q}} \ right) \ sin \ left ({\ frac {(2p-1) \ pi k} {q}} \ right) \ right]}

se aplică tuturor $1\leq p\leq q$ ${\ displaystyle 1 \ leq p \ leq q}$ ${\ displaystyle 1 \ leq p \ leq q}$ . $C_{\nu }(x)$ ${\ displaystyle C _ {\ nu} (x)}$ ${\ displaystyle C _ {\ nu} (x)}$ Și $S_{\nu }(x)$ ${\ displaystyle S _ {\ nu} (x)}$ ${\ displaystyle S _ {\ nu} (x)}$ sunt definite prin intermediul funcției chi a lui Legendre $\chi _{\nu }$ ${\ displaystyle \ chi _ {\ nu}}$ ${\ displaystyle \ chi _ {\ nu}}$ ,

C_{\nu }(x)=\operatorname {Re} \,\chi _{\nu }(e^{ix})

{\ displaystyle C _ {\ nu} (x) = \ operatorname {Re} \, \ chi _ {\ nu} (e ^ {ix})}

{\ displaystyle C _ {\ nu} (x) = \ operatorname {Re} \, \ chi _ {\ nu} (e ^ {ix})}

Și

S_{\nu }(x)=\operatorname {Im} \,\chi _{\nu }(e^{ix}).

{\ displaystyle S _ {\ nu} (x) = \ operatorname {Im} \, \ chi _ {\ nu} (e ^ {ix}).}

{\ displaystyle S _ {\ nu} (x) = \ operatorname {Im} \, \ chi _ {\ nu} (e ^ {ix}).}

Pentru valori întregi ale $\nu$ ${\ displaystyle \ nu}$ $\ nu$ , poate fi exprimat în termeni de polinoame ale lui Euler. Aceste relații pot fi derivate folosind ecuația funcțională împreună cu formula Hurwitz.

Extinderi de serie

Seria Taylor

Derivata funcției Hurwitz zeta față de a doua variabilă este o traducere:

{\frac {\partial }{\partial q}}\zeta (s,q)=-s\zeta (s+1,q).

{\ displaystyle {\ frac {\ partial} {\ partial q}} \ zeta (s, q) = - s \ zeta (s + 1, q).}

{\ displaystyle {\ frac {\ partial} {\ partial q}} \ zeta (s, q) = - s \ zeta (s + 1, q).}

Prin urmare, seria Taylor are forma umbrală caracteristică:

\zeta (s,x+y)=\sum _{k=0}^{\infty }{\frac {y^{k}}{k!}}{\frac {\partial ^{k}}{\partial x^{k}}}\zeta (s,x)=\sum _{k=0}^{\infty }{s+k-1 \choose s-1}(-y)^{k}\zeta (s+k,x).

{\ displaystyle \ zeta (s, x + y) = \ sum _ {k = 0} ^ {\ infty} {\ frac {y ^ {k}} {k!}} {\ frac {\ partial ^ {k }} {\ partial x ^ {k}}} \ zeta (s, x) = \ sum _ {k = 0} ^ {\ infty} {s + k-1 \ choose s-1} (- y) ^ {k} \ zeta (s + k, x).}

{\ displaystyle \ zeta (s, x + y) = \ sum _ {k = 0} ^ {\ infty} {\ frac {y ^ {k}} {k!}} {\ frac {\ partial ^ {k }} {\ partial x ^ {k}}} \ zeta (s, x) = \ sum _ {k = 0} ^ {\ infty} {s + k-1 \ choose s-1} (- y) ^ {k} \ zeta (s + k, x).}

Alternativ,

\zeta (s,q)={\frac {1}{q^{s}}}+\sum _{n=0}^{\infty }(-q)^{n}{s+n-1 \choose n}\zeta (s+n),

{\ displaystyle \ zeta (s, q) = {\ frac {1} {q ^ {s}}} + \ sum _ {n = 0} ^ {\ infty} (- q) ^ {n} {s + n-1 \ alege n} \ zeta (s + n),}

{\ displaystyle \ zeta (s, q) = {\ frac {1} {q ^ {s}}} + \ sum _ {n = 0} ^ {\ infty} (- q) ^ {n} {s + n-1 \ alege n} \ zeta (s + n),}

cu $|q|<1$ ${\ displaystyle | q | <1}$ ${\ displaystyle | q | <1}$ . ^[6]

Strâns legată este formula Stark - Keiper :

\zeta (s,N)=\sum _{k=0}^{\infty }\left[N+{\frac {s-1}{k+1}}\right]{s+k-1 \choose s-1}(-1)^{k}\zeta (s+k,N)

{\ displaystyle \ zeta (s, N) = \ sum _ {k = 0} ^ {\ infty} \ left [N + {\ frac {s-1} {k + 1}} \ right] {s + k - 1 \ alege s-1} (- 1) ^ {k} \ zeta (s + k, N)}

{\ displaystyle \ zeta (s, N) = \ sum _ {k = 0} ^ {\ infty} \ left [N + {\ frac {s-1} {k + 1}} \ right] {s + k - 1 \ alege s-1} (- 1) ^ {k} \ zeta (s + k, N)}

care se aplică la $Nu.$ ${\ displaystyle N}$ $Nu.$ întreg și $s$ ${\ displaystyle s}$ $s$ arbitrar. A se vedea formula lui Faulhaber pentru o relație similară asupra sumelor finite de puteri ale numerelor întregi.

Seria Laurent

Extinderea seriei lui Laurent poate fi utilizată pentru a defini constantele Stieltjes care apar în serie

\zeta (s,q)={\frac {1}{s-1}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}\gamma _{n}(q)\;(s-1)^{n}.

{\ displaystyle \ zeta (s, q) = {\ frac {1} {s-1}} + \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n}} {n!}} \ gamma _ {n} (q) \; (s-1) ^ {n}.}

{\ displaystyle \ zeta (s, q) = {\ frac {1} {s-1}} + \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n}} {n!}} \ gamma _ {n} (q) \; (s-1) ^ {n}.}

În special, $\gamma _{0}(q)=-\psi (q)$ ${\ displaystyle \ gamma _ {0} (q) = - \ psi (q)}$ ${\ displaystyle \ gamma _ {0} (q) = - \ psi (q)}$ Și $\gamma _{0}(1)=-\psi (1)=\gamma _{0}=\gamma$ ${\ displaystyle \ gamma _ {0} (1) = - \ psi (1) = \ gamma _ {0} = \ gamma}$ ${\ displaystyle \ gamma _ {0} (1) = - \ psi (1) = \ gamma _ {0} = \ gamma}$ .

Legături cu alte funcții

Legătură cu polinoamele Bernoulli

Functia $\beta$ ${\ displaystyle \ beta}$ $\ beta$ definit mai sus generalizează polinoamele Bernoulli :

B_{n}(x)=-\Re \left[(-i)^{n}\beta (x;n)\right]

{\ displaystyle B_ {n} (x) = - \ Re \ left [(- i) ^ {n} \ beta (x; n) \ right]}

{\ displaystyle B_ {n} (x) = - \ Re \ left [(- i) ^ {n} \ beta (x; n) \ right]}

unde este $\Re (z)$ ${\ displaystyle \ Re (z)}$ ${\ displaystyle \ Re (z)}$ indică partea reală a $z$ ${\ displaystyle z}$ $z$ . Alternativ,

\zeta (-n,x)=-{B_{n+1}(x) \over n+1}.

{\ displaystyle \ zeta (-n, x) = - {B_ {n + 1} (x) \ peste n + 1}.}

{\ displaystyle \ zeta (-n, x) = - {B_ {n + 1} (x) \ peste n + 1}.}

În special, relația este valabilă $n=0$ ${\ displaystyle n = 0}$ $n = 0$ si tu ai

\zeta (0,x)={\frac {1}{2}}-x.

{\ displaystyle \ zeta (0, x) = {\ frac {1} {2}} - x.}

{\ displaystyle \ zeta (0, x) = {\ frac {1} {2}} - x.}

Legătură cu funcția theta Jacobi

De sine $\vartheta (z,\tau )$ ${\ displaystyle \ vartheta (z, \ tau)}$ ${\ displaystyle \ vartheta (z, \ tau)}$ este funcția theta Jacobi, atunci

\int _{0}^{\infty }\left[\vartheta (z,it)-1\right]t^{s/2}{\frac {dt}{t}}=\pi ^{-(1-s)/2}\Gamma \left({\frac {1-s}{2}}\right)\left[\zeta (1-s,z)+\zeta (1-s,1-z)\right]

{\ displaystyle \ int _ {0} ^ {\ infty} \ left [\ vartheta (z, it) -1 \ right] t ^ {s / 2} {\ frac {dt} {t}} = \ pi ^ {- (1-s) / 2} \ Gamma \ left ({\ frac {1-s} {2}} \ right) \ left [\ zeta (1-s, z) + \ zeta (1-s, 1-z) \ dreapta]}

{\ displaystyle \ int _ {0} ^ {\ infty} \ left [\ vartheta (z, it) -1 \ right] t ^ {s / 2} {\ frac {dt} {t}} = \ pi ^ {- (1-s) / 2} \ Gamma \ left ({\ frac {1-s} {2}} \ right) \ left [\ zeta (1-s, z) + \ zeta (1-s, 1-z) \ dreapta]}

se aplică la $\operatorname {Re} (s)>0$ ${\ displaystyle \ operatorname {Re} (s)> 0}$ ${\ displaystyle \ operatorname {Re} (s)> 0}$ Și $z$ ${\ displaystyle z}$ $z$ complex, dar nu întreg. Pentru $z$ ${\ displaystyle z}$ $z$ întreg, formula devine

\int _{0}^{\infty }\left[\vartheta (n,it)-1\right]t^{s/2}{\frac {dt}{t}}=2\ \pi ^{-(1-s)/2}\ \Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s)=2\ \pi ^{-s/2}\ \Gamma \left({\frac {s}{2}}\right)\zeta (s).

{\ displaystyle \ int _ {0} ^ {\ infty} \ left [\ vartheta (n, it) -1 \ right] t ^ {s / 2} {\ frac {dt} {t}} = 2 \ \ pi ^ {- (1-s) / 2} \ \ Gamma \ left ({\ frac {1-s} {2}} \ right) \ zeta (1-s) = 2 \ \ pi ^ {- s / 2} \ \ Gamma \ left ({\ frac {s} {2}} \ right) \ zeta (s).}

{\ displaystyle \ int _ {0} ^ {\ infty} \ left [\ vartheta (n, it) -1 \ right] t ^ {s / 2} {\ frac {dt} {t}} = 2 \ \ pi ^ {- (1-s) / 2} \ \ Gamma \ left ({\ frac {1-s} {2}} \ right) \ zeta (1-s) = 2 \ \ pi ^ {- s / 2} \ \ Gamma \ left ({\ frac {s} {2}} \ right) \ zeta (s).}

unde este $\zeta$ ${\ displaystyle \ zeta}$ $\ zeta$ este funcția zeta Riemann . Rețineți că această ultimă formă este ecuația funcțională a funcției zeta Riemann, așa cum a fost scrisă inițial de Riemann. Distincția dintre $z$ ${\ displaystyle z}$ $z$ întreg și nu ține cont de faptul că funcția theta a lui Jacobi converge la funcția delta a lui Dirac în $z$ ${\ displaystyle z}$ $z$ de sine $t\rightarrow 0$ ${\ displaystyle t \ rightarrow 0}$ ${\ displaystyle t \ rightarrow 0}$ .

Legătură cu funcțiile Dirichlet L

Dacă argumentul este un număr rațional, funcția zeta Hurwitz poate fi exprimată ca o combinație liniară a funcțiilor Dirichlet L și invers: Zeta lui Hurwitz coincide cu Zeta lui Riemann $\zeta (s)$ ${\ displaystyle \ zeta (s)}$ $\ zeta (e)$ cand $q=1$ ${\ displaystyle q = 1}$ $q = 1$ , de sine $q=1/2$ ${\ displaystyle q = 1/2}$ ${\ displaystyle q = 1/2}$ Este egal cu $(2^{s}-1)\zeta (s)$ ${\ displaystyle (2 ^ {s} -1) \ zeta (s)}$ ${\ displaystyle (2 ^ {s} -1) \ zeta (s)}$ , ^[7] și dacă $q=n/k$ ${\ displaystyle q = n / k}$ ${\ displaystyle q = n / k}$ cu $k>2$ ${\ displaystyle k> 2}$ ${\ displaystyle k> 2}$ , $(n,k)>1$ ${\ displaystyle (n, k)> 1}$ ${\ displaystyle (n, k)> 1}$ Și $0<n<k$ ${\ displaystyle 0 <n <k}$ ${\ displaystyle 0 <n <k}$ , apoi ^[8]

\zeta (s,n/k)={\frac {k^{s}}{\varphi (k)}}\sum _{\chi }{\overline {\chi }}(n)L(s,\chi ),

{\ displaystyle \ zeta (s, n / k) = {\ frac {k ^ {s}} {\ varphi (k)}} \ sum _ {\ chi} {\ overline {\ chi}} (n) L (s, \ chi),}

{\ displaystyle \ zeta (s, n / k) = {\ frac {k ^ {s}} {\ varphi (k)}} \ sum _ {\ chi} {\ overline {\ chi}} (n) L (s, \ chi),}

unde suma este pe caracterele lui Dirichlet mod $k$ ${\ displaystyle k}$ $k$ . În direcția opusă avem combinația liniară ^[7]

L(s,\chi )={\frac {1}{k^{s}}}\sum _{n=1}^{k}\chi (n)\;\zeta \left(s,{\frac {n}{k}}\right).

{\ displaystyle L (s, \ chi) = {\ frac {1} {k ^ {s}}} \ sum _ {n = 1} ^ {k} \ chi (n) \; \ zeta \ left (s , {\ frac {n} {k}} \ right).}

{\ displaystyle L (s, \ chi) = {\ frac {1} {k ^ {s}}} \ sum _ {n = 1} ^ {k} \ chi (n) \; \ zeta \ left (s , {\ frac {n} {k}} \ right).}

Există, de asemenea, teorema multiplicării

k^{s}\zeta (s)=\sum _{n=1}^{k}\zeta \left(s,{\frac {n}{k}}\right),

{\ displaystyle k ^ {s} \ zeta (s) = \ sum _ {n = 1} ^ {k} \ zeta \ left (s, {\ frac {n} {k}} \ right),}

{\ displaystyle k ^ {s} \ zeta (s) = \ sum _ {n = 1} ^ {k} \ zeta \ left (s, {\ frac {n} {k}} \ right),}

dintre care o generalizare utilă este relația de distribuție ^[9]

\sum _{p=0}^{q-1}\zeta (s,a+p/q)=q^{s}\,\zeta (s,qa).

{\ displaystyle \ sum _ {p = 0} ^ {q-1} \ zeta (s, a + p / q) = q ^ {s} \, \ zeta (s, qa).}

{\ displaystyle \ sum _ {p = 0} ^ {q-1} \ zeta (s, a + p / q) = q ^ {s} \, \ zeta (s, qa).}

(Acest ultim formular este valabil numai dacă $q$ ${\ displaystyle q}$ $q$ este un număr natural și $1-qa$ ${\ displaystyle 1-qa}$ ${\ displaystyle 1-qa}$ nu este.)

Zero

De sine $q=1$ ${\ displaystyle q = 1}$ $q = 1$ , funcția zeta Hurwitz este redusă la funcția zeta Riemann ; de sine $q=1/2$ ${\ displaystyle q = 1/2}$ ${\ displaystyle q = 1/2}$ se reduce la funcția zeta Riemann înmulțită cu o funcție simplă variabilă complexă $s$ ${\ displaystyle s}$ $s$ ( vezi mai sus ), referindu-se în orice caz la studiul dificil al zerourilor din Zeta lui Riemann. În special, nu există zerouri cu o parte reală mai mare sau egală cu 1. Cu toate acestea, dacă $0<q<1$ ${\ displaystyle 0 <q <1}$ $0 <q <1$ Și $q\neq 1/2$ ${\ displaystyle q \ neq 1/2}$ ${\ displaystyle q \ neq 1/2}$ , apoi există zerouri ale funcției zeta Hurwitz în bandă $1<\operatorname {Re} (s)<1+\epsilon$ ${\ displaystyle 1 <\ operatorname {Re} (s) <1+ \ epsilon}$ ${\ displaystyle 1 <\ operatorname {Re} (s) <1+ \ epsilon}$ pentru fiecare $\epsilon$ ${\ displaystyle \ epsilon}$ $\ epsilon$ real pozitiv. Acest fapt a fost dovedit de Davenport și Heilbronn pentru $q$ ${\ displaystyle q}$ $q$ rațional sau transcendent ^[10] și de Cassels pentru iraționalele algebrice. ^[7] ^[11]

Aplicații

Funcția zeta Hurwitz apare în diferite discipline. Cel mai frecvent, apare în teoria numerelor , unde studiul său este cel mai profund și dezvoltat. Cu toate acestea, apare și în studiul fractalelor și al sistemelor dinamice . În statisticile aplicate, este prezent în legea Zipf și în Zipf - legea lui Mandelbrot. În fizica particulelor , apare într-o formulă Julian Schwinger , ^[12] oferind un rezultat exact al ratei de producție a cuplului unui electron Dirac .

Cazuri speciale și generalizări

Funcția zeta Hurwitz cu $m$ ${\ displaystyle m}$ $m$ un număr întreg pozitiv este legat de funcția poligamă :

\psi ^{(m)}(z)=(-1)^{m+1}m!\zeta (m+1,z)\ .

{\ displaystyle \ psi ^ {(m)} (z) = (- 1) ^ {m + 1} m! \ zeta (m + 1, z) \.}

{\ displaystyle \ psi ^ {(m)} (z) = (- 1) ^ {m + 1} m! \ zeta (m + 1, z) \.}

Pentru numere întregi negative $-n$ ${\ displaystyle -n}$ $-n$ , valorile sunt legate de polinoamele Bernoulli : ^[13]

\zeta (-n,x)=-{\frac {B_{n+1}(x)}{n+1}}\ .

{\ displaystyle \ zeta (-n, x) = - {\ frac {B_ {n + 1} (x)} {n + 1}} \.}

{\ displaystyle \ zeta (-n, x) = - {\ frac {B_ {n + 1} (x)} {n + 1}} \.}

Funcția zeta a lui Barnes generalizează zeta lui Hurwitz ca

\zeta _{N}(s,w|a_{1},...,a_{N})=\sum _{n_{1},\dots ,n_{N}\geq 0}{\frac {1}{(w+n_{1}a_{1}+\cdots +n_{N}a_{N})^{s}}}

{\ displaystyle \ zeta _ {N} (s, w | a_ {1}, ..., a_ {N}) = \ sum _ {n_ {1}, \ dots, n_ {N} \ geq 0} { \ frac {1} {(w + n_ {1} a_ {1} + \ cdots + n_ {N} a_ {N}) ^ {s}}}}

{\ displaystyle \ zeta _ {N} (s, w | a_ {1}, ..., a_ {N}) = \ sum _ {n_ {1}, \ dots, n_ {N} \ geq 0} { \ frac {1} {(w + n_ {1} a_ {1} + \ cdots + n_ {N} a_ {N}) ^ {s}}}}

unde este $w$ ${\ displaystyle w}$ $w$ Și $a_{j}$ ${\ displaystyle a_ {j}}$ ${\ displaystyle a_ {j}}$ au o parte pozitivă și reală $\operatorname {Re} (s)>N$ ${\ displaystyle \ operatorname {Re} (s)> N}$ ${\ displaystyle \ operatorname {Re} (s)> N}$ .

O altă generalizare vine din funcția transcendentă a lui Lerch :

\Phi (z,s,q)=\sum _{k=0}^{\infty }{\frac {z^{k}}{(k+q)^{s}}}

{\ displaystyle \ Phi (z, s, q) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {(k + q) ^ {s}}}}

{\ displaystyle \ Phi (z, s, q) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {(k + q) ^ {s}}}}

prin urmare

\zeta (s,q)=\Phi (1,s,q).\,

{\ displaystyle \ zeta (s, q) = \ Phi (1, s, q). \,}

{\ displaystyle \ zeta (s, q) = \ Phi (1, s, q). \,}

În cele din urmă, apare funcția hipergeometrică

\zeta (s,a)=a^{-s}\cdot {}_{s+1}F_{s}(1,a_{1},a_{2},\ldots a_{s};a_{1}+1,a_{2}+1,\ldots a_{s}+1;1)

{\ displaystyle \ zeta (s, a) = a ^ {- s} \ cdot {} _ {s + 1} F_ {s} (1, a_ {1}, a_ {2}, \ ldots a_ {s} ; a_ {1} + 1, a_ {2} +1, \ ldots a_ {s} +1; 1)}

{\ displaystyle \ zeta (s, a) = a ^ {- s} \ cdot {} _ {s + 1} F_ {s} (1, a_ {1}, a_ {2}, \ ldots a_ {s} ; a_ {1} + 1, a_ {2} +1, \ ldots a_ {s} +1; 1)}

unde este

a_{1}=a_{2}=\ldots =a_{s}=a{\text{, }}a\notin \mathbb {N} {\text{ e  }}s\in \mathbb {N} ^{+}.

{\ displaystyle a_ {1} = a_ {2} = \ ldots = a_ {s} = a {\ text {,}} a \ notin \ mathbb {N} {\ text {e}} s \ in \ mathbb { N} ^ {+}.}

{\ displaystyle a_ {1} = a_ {2} = \ ldots = a_ {s} = a {\ text {,}} a \ notin \ mathbb {N} {\ text {e}} s \ in \ mathbb { N} ^ {+}.}

și funcția Meijer G.

\zeta (s,a)=G\,_{s+1,\,s+1}^{\,1,\,s+1}\left(-1\;\left|\;{\begin{matrix}0,1-a,\ldots ,1-a\\0,-a,\ldots ,-a\end{matrix}}\right)\right.\qquad s\in \mathbb {N} ^{+}.

{\ displaystyle \ zeta (s, a) = G \, _ {s + 1, \, s + 1} ^ {\, 1, \, s + 1} \ left (-1 \; \ left | \; {\ begin {matrix} 0,1-a, \ ldots, 1-a \\ 0, -a, \ ldots, -a \ end {matrix}} \ right) \ right. \ qquad s \ in \ mathbb { N} ^ {+}.}

{\ displaystyle \ zeta (s, a) = G \, _ {s + 1, \, s + 1} ^ {\, 1, \, s + 1} \ left (-1 \; \ left | \; {\ begin {matrix} 0,1-a, \ ldots, 1-a \\ 0, -a, \ ldots, -a \ end {matrix}} \ right) \ right. \ qquad s \ in \ mathbb { N} ^ {+}.}

Notă

^ https://nbviewer.jupyter.org/github/empet/Math/blob/master/DomainColoring.ipynb
^ Helmut Hasse, Ein Summierungsverfahren für die Riemannsche ζ-Reihe , în Mathematische Zeitschrift , vol. 32, nr. 1, 1930, pp. 458–464, DOI : 10.1007 / BF01194645 , JFM 56.0894.03 .
^ Iaroslav V. Blagouchine, Three Notes on Ser's and Hasse's Representations for the Zeta-functions , in Integers (Electronic Journal of Combinatorial Number Theory) , 18A, 2018, pp. 1–45, Bibcode : 2016arXiv160602044B , arXiv : 1606.02044 .
^ A se vedea, de exemplu, Anexa B a IV-ului Blagouchine, o teoremă pentru evaluarea în formă închisă a primei constante Stieltjes generalizate la argumente raționale și câteva rezumări conexe , în Journal of Number Theory , vol. 148, Elsevier, 2014, p. 537–592, DOI : 10.1016 / j.jnt.2014.08.009 , arXiv : 1401.3724 .
^ Furnizat de Djurdje Cvijović și Jacek Klinowski, Valori ale funcțiilor zeta Legendre chi și Hurwitz la argumente raționale , în Mathematics of Computation , vol. 68, nr. 228, 1999, pp. 1623–1630, Bibcode : 1999MaCom..68.1623C , DOI : 10.1090 / S0025-5718-99-01091-1 .
^ Linas Vepstas, Un algoritm eficient pentru accelerarea convergenței seriilor oscilatorii, util pentru calcularea polilogaritmului și a funcțiilor zeta Hurwitz , în Algoritmi numerici , vol. 47, 2007, pp. 211–252, Bibcode : 2008NuAlg..47..211V , DOI : 10.1007 / s11075-007-9153-8 , arXiv : math / 0702243 .
^ ^a ^b ^c Davenport (1967) p.73
^ David Lowry, Hurwitz Zeta este o sumă de funcții L Dirichlet și invers , în mixmath . Adus de douăzeci și unu iunie 2018.
^ Daniel S. Kubert și Serge Lang , Modular Units , Grundlehren der Mathematischen Wissenschaften, vol. 244, Springer-Verlag , 1981, p. 13 , ISBN 0-387-90517-0 , Zbl 0492.12002 .
^ H. Davenport și H. Heilbronn, Despre zerourile anumitor serii Dirichlet , în Journal of the London Mathematical Society , vol. 11, n. 3, 1936, pp. 181–185, DOI : 10.1112 / jlms / s1-11.3.181 , Zbl 0014.21601 .
^ JWS Cassels, Footnote to a note of Davenport and Heilbronn , in Journal of the London Mathematical Society , vol. 36, n. 1, 1961, pp. 177–184, DOI : 10.1112 / jlms / s1-36.1.177 , Zbl 0097.03403 .
^ J. Schwinger, Despre invarianța gabaritului și polarizarea în vid , în Physical Review , vol. 82, nr. 5, 1951, pp. 664–679, Bibcode : 1951PhRv ... 82..664S , DOI : 10.1103 / PhysRev.82.664 .
^ Apostol (1976) p.264

Bibliografie

Apostol, TM (2010), „Funcția zeta Hurwitz” , în Olver, Frank WJ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0521192255 , MR 2723248
vezi capitolul 12 din Apostol, TM (1976), Introducere în teoria numerelor analitice, Texte de licență în matematică, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3 , MR 0434929 , Zbl 0335.10001
Milton Abramowitz și Irene A. Stegun, Manual de funcții matematice , (1964) Dover Publications, New York. ISBN 0-486-61272-4 . (a se vedea secțiunea 6.4.10 pentru relația cu funcția poligamă.)
Harold Davenport , Teoria multiplicativă a numerelor , Prelegeri de matematică avansată, vol. 1, Chicago, Markham, 1967, Zbl 0159.06303 .
Jeff Miller e Victor S. Adamchik, Derivatives of the Hurwitz Zeta Function for Rational Arguments , in Journal of Computational and Applied Mathematics , vol. 100, 1998, pp. 201–206, DOI : 10.1016/S0377-0427(98)00193-9 .
Linas Vepstas, The Bernoulli Operator, the Gauss–Kuzmin–Wirsing Operator, and the Riemann Zeta ( PDF ), su linas.org .
István Mező e Ayhan Dil, Hyperharmonic series involving Hurwitz zeta function , in Journal of Number Theory , vol. 130, n. 2, 2010, pp. 360–369, DOI : 10.1016/j.jnt.2009.08.005 .

Voci correlate

Collegamenti esterni

( EN ) Eric W. Weisstein, Funzione zeta di Hurwitz , in MathWorld , Wolfram Research.

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[1] ttps://nbviewer.jupyter.org/github/empet/Math/blob/master/DomainColoring.ipynb

[2] Helmut Hasse, Ein Summierungsverfahren für die Riemannsche ζ-Reihe , în Mathematische Zeitschrift , vol. 32, nr. 1, 1930, pp. 458–464, DOI : 10.1007 / BF01194645 , JFM 56.0894.03 .

[3] Iaroslav V. Blagouchine, Three Notes on Ser's and Hasse's Representations for the Zeta-functions , in Integers (Electronic Journal of Combinatorial Number Theory) , 18A, 2018, pp. 1–45, Bibcode : 2016arXiv160602044B , arXiv : 1606.02044 .

[4] A se vedea, de exemplu, Anexa B a IV-ului Blagouchine, o teoremă pentru evaluarea în formă închisă a primei constante Stieltjes generalizate la argumente raționale și câteva rezumări conexe , în Journal of Number Theory , vol. 148, Elsevier, 2014, p. 537–592, DOI : 10.1016 / j.jnt.2014.08.009 , arXiv : 1401.3724 .

[5] Furnizat de Djurdje Cvijović și Jacek Klinowski, Valori ale funcțiilor zeta Legendre chi și Hurwitz la argumente raționale , în Mathematics of Computation , vol. 68, nr. 228, 1999, pp. 1623–1630, Bibcode : 1999MaCom..68.1623C , DOI : 10.1090 / S0025-5718-99-01091-1 .

[6] Linas Vepstas, Un algoritm eficient pentru accelerarea convergenței seriilor oscilatorii, util pentru calcularea polilogaritmului și a funcțiilor zeta Hurwitz , în Algoritmi numerici , vol. 47, 2007, pp. 211–252, Bibcode : 2008NuAlg..47..211V , DOI : 10.1007 / s11075-007-9153-8 , arXiv : math / 0702243 .

[Dav73-7] Davenport (1967) p.73

[MM13-8] David Lowry, Hurwitz Zeta este o sumă de funcții L Dirichlet și invers , în mixmath . Adus de douăzeci și unu iunie 2018.

[9] Daniel S. Kubert și Serge Lang , Modular Units , Grundlehren der Mathematischen Wissenschaften, vol. 244, Springer-Verlag , 1981, p. 13 , ISBN 0-387-90517-0 , Zbl 0492.12002 .

[10] H. Davenport și H. Heilbronn, Despre zerourile anumitor serii Dirichlet , în Journal of the London Mathematical Society , vol. 11, n. 3, 1936, pp. 181–185, DOI : 10.1112 / jlms / s1-11.3.181 , Zbl 0014.21601 .

[11] JWS Cassels, Footnote to a note of Davenport and Heilbronn , in Journal of the London Mathematical Society , vol. 36, n. 1, 1961, pp. 177–184, DOI : 10.1112 / jlms / s1-36.1.177 , Zbl 0097.03403 .

[12] J. Schwinger, Despre invarianța gabaritului și polarizarea în vid , în Physical Review , vol. 82, nr. 5, 1951, pp. 664–679, Bibcode : 1951PhRv ... 82..664S , DOI : 10.1103 / PhysRev.82.664 .

[Ap264-13] Apostol (1976) p.264

[1]

[2] a

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]