Imagini conforme

Teselare regulată a vârfului

Imagine conformă obținută printr-un polinom de grad

4

{\ displaystyle 4}

4

Imaginile conforme sunt obținute ca urmare a aplicării unei hărți conforme (o transformare a planului care păstrează unghiurile) la o imagine de pornire. În acest fel, se realizează o deformare a imaginii inițiale, care face posibilă vizualizarea efectelor unei hărți conforme pe un subset al planului: acestea sunt efecte greu de înțeles în orice alt mod, deoarece implică contorul -reprezentare mentală intuitivă.într-un spațiu cu patru dimensiuni, o reprezentare care scapă de intuiția spațială tridimensională normală.

Tehnica imaginii conforme este o generalizare a sistemului analog de colorare a domeniului , utilizată și pentru a vizualiza efectul hărților conforme. Dar, în timp ce acesta din urmă folosește un cerc cromatic prefixat format din culori infinite, tehnica conformării imaginilor folosește o teselare a planului realizată cu imagini finite. Interesul didactic-pedagogic al acestei abordări se datorează posibilității de a aplica metoda unui flux de imagini provenind de la o cameră web pentru a permite o interactivitate mai mare și o buclă de feedback mai bogată ^[1] .

(În restul articolului, termenii „desen” sau „figură” vor fi folosiți în loc de „imagine”, pentru a evita confuzia terminologică cu conceptele matematice de imagine și imagine contrară a unei funcții. partea de sus este un ceas centrat în origine, înconjurat de o propoziție ^[2] și inscripționat într-un pătrat).

Hărți conforme

Același subiect în detaliu: hartă conformă .

Planificați teselate de figura unui ceas

Aplicarea pe planul teselat al unei comparații :

z\mapsto az+b

{\ displaystyle z \ mapsto az + b}

{\ displaystyle z \ mapsto az + b}

O hartă conformală este o transformare plană care păstrează unghiuri. Acestea îndeplinesc, de exemplu, multe funcții de utilizare obișnuită, dacă sunt luate în considerare în câmpul complex: l ' exponențiere , l' exponențială , logaritmul , tangenta .

Planul poate fi parametrizat folosind coordonate carteziene unde fiecare punct este notat ca $(x,y)\in \mathbb {R} ^{2}$ ${\ displaystyle (x, y) \ in \ mathbb {R} ^ {2}}$ ${\ displaystyle (x, y) \ in \ mathbb {R} ^ {2}}$ , dar pentru hărțile conforme este mai simplu și mai convenabil să se utilizeze formalismul analizei complexe : în acest context, planul cartezian este înlocuit de planul complex , în ale cărui puncte, notat ca $x+i\,y\in \mathbb {C}$ ${\ displaystyle x + i \, y \ in \ mathbb {C}}$ ${\ displaystyle x + i \, y \ in \ mathbb {C}}$ , se aplică operațiile algebrice normale ale câmpului complex .

Operând în acest mod, se obține o simplificare datorită faptului că, în planul complex, o omotitate a relației $r$ ${\ displaystyle r}$ $r$ se obține cu o multiplicare simplă cu numărul real $r$ ${\ displaystyle r}$ $r$ , în timp ce o rotație a unghiului $\theta$ ${\ displaystyle \ theta}$ $\ theta$ se exprimă ca o simplă multiplicare cu numărul complex al unității $e^{i\theta }$ ${\ displaystyle e ^ {i \ theta}}$ ${\ displaystyle e ^ {i \ theta}}$ . Aceste două cazuri simple pot fi combinate atunci când este vorba de multiplicarea cu orice număr complex: $a=r\,e^{i\theta }$ ${\ displaystyle a = r \, e ^ {i \ theta}}$ ${\ displaystyle a = r \, e ^ {i \ theta}}$ este o operație algebrică în câmpul complex care, pe plan cartezian , se traduce printr-o roto-omotezie: adică este combinația dintre o rotație și o omotetie, o transformare a planului numită altfel similitudine . Din considerații algebrice simple asupra modulelor numerelor complexe implicate, rezultă că numărul complex $a=r\,e^{i\theta }$ ${\ displaystyle a = r \, e ^ {i \ theta}}$ ${\ displaystyle a = r \, e ^ {i \ theta}}$ reprezintă factorul de zoom al transformării plane .

Acest formalism, cu operațiile sale algebrice, permite unificarea a două concepte diferite într-unul singur, numărul complex, care reprezintă atât punctele planului ( $z$ ${\ displaystyle z}$ $z$ a funcției $z\mapsto az$ ${\ displaystyle z \ mapsto az}$ ${\ displaystyle z \ mapsto az}$ ) și asemănările care acționează asupra punctelor (coeficientul $la$ ${\ displaystyle a}$ $la$ a funcției $z\mapsto az$ ${\ displaystyle z \ mapsto az}$ ${\ displaystyle z \ mapsto az}$ )

Funcții holomorfe

Același subiect în detaliu: funcțiile holomorfe .

În cadrul hărților conforme , o anumită clasă este constituită de funcțiile holomorfe : acestea din urmă sunt conforme în toate punctele în care derivata nu dispare. Conformitatea în aceste puncte derivă din faptul că pot fi aproximate local printr-o comparație:

$f(z)=a\,(z-z_{0})+b+o(z-z_{0})$ ${\ displaystyle f (z) = a \, (z-z_ {0}) + b + o (z-z_ {0})}$ ${\ displaystyle f (z) = a \, (z-z_ {0}) + b + o (z-z_ {0})}$

În această expresie, $a=f'(z_{0})$ ${\ displaystyle a = f '(z_ {0})}$ ${\ displaystyle a = f '(z_ {0})}$ este derivatul lui $f(z)$ ${\ displaystyle f (z)}$ $f (z)$ în sens $z_{0}$ ${\ displaystyle z_ {0}}$ $z_0$ , in timp ce $b=f(z_{0})$ ${\ displaystyle b = f (z_ {0})}$ ${\ displaystyle b = f (z_ {0})}$ este valoarea asumată de $f(z)$ ${\ displaystyle f (z)}$ $f (z)$ în $z_{0}$ ${\ displaystyle z_ {0}}$ $z_ {0}$ . Comportamentul local al funcției poate fi aproximat cu un monomiu de gradul I. Termenul $o(z-z_{0})$ ${\ displaystyle o (z-z_ {0})}$ ${\ displaystyle o (z-z_ {0})}$ în schimb, reprezintă eroarea acestei aproximări, neglijabilă ( sau mică ) atunci când se tinde spre zero de $z-z_{0}$ ${\ displaystyle z-z_ {0}}$ ${\ displaystyle z-z_ {0}}$ . Din această expresie se poate observa că factorul de scală al omotentei este reprezentat tocmai de modulul valorii complexe a derivatei de $f$ ${\ displaystyle f}$ $f$ , unde acest lucru este diferit de zero. La zerourile derivatei, funcția nu mai este conformă și poate fi aproximată local cu un monomial de grad mai mare decât $1$ ${\ displaystyle 1}$ $1$ .

Funcții polinomiale

Similele, exprimate prin polinoame de gradul I, au derivate constante și sunt cele mai simple exemple de funcții holomorfe. După simile, cele mai simple exemple de holomorfie sunt cu polinoame de grad superior ( $k>1$ ${\ displaystyle k> 1}$ ${\ displaystyle k> 1}$ ) și, în special, cu monomii de acest tip $z\mapsto z^{k}$ ${\ displaystyle z \ mapsto z ^ {k}}$ ${\ displaystyle z \ mapsto z ^ {k}}$ . Derivatul monomial este $z\mapsto k\,z^{k-1}$ ${\ displaystyle z \ mapsto k \, z ^ {k-1}}$ ${\ displaystyle z \ mapsto k \, z ^ {k-1}}$ , că pentru $k>1$ ${\ displaystyle k> 1}$ ${\ displaystyle k> 1}$ dispare doar la origine: funcția planului în sine asociată cu monomiul de ordin superior a $1$ ${\ displaystyle 1}$ $1$ este în conformitate cu toate punctele, cu excepția originii.

O problemă care apare atunci când se dorește reprezentarea funcțiilor holomorfe constă în faptul că, în general, acestea nu sunt funcții injective : de exemplu, deja pentru monomiul simplu $z^{k}$ ${\ displaystyle z ^ {k}}$ $z ^ {k}$ (cu $k>1$ ${\ displaystyle k> 1}$ ${\ displaystyle k> 1}$ ) există $k$ ${\ displaystyle k}$ $k$ puncte diferite care sunt trimise în aceeași valoare $y$ ${\ displaystyle y}$ $y$ , cu singura excepție, desigur, a întâmplării $y=0$ ${\ displaystyle y = 0}$ ${\ displaystyle y = 0}$ : de exemplu, la punctul $y=1$ ${\ displaystyle y = 1}$ ${\ displaystyle y = 1}$ toate $k$ ${\ displaystyle k}$ $k$ rădăcini $k$ ${\ displaystyle k}$ $k$ -thth din unitate .

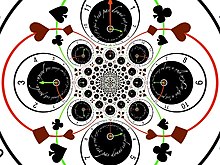
Lipsa injectivității are efecte importante la vizualizarea figurilor conforme. Deja dacă luăm în considerare, de exemplu, transformarea constând dintr-un simplu pătrat și o aplicăm planului teselat din proiectarea ceasului, obținem o figură în care există suprapunerea a două teselări diferite: de fapt, deși a spus înainte, în fiecare punct al rezultatului, cu excepția zero, sunt mapate două puncte ale originalului. Rezultatul este următoarea figură neclară:

Un ceas „pătrat”. Rețineți dubla suprapunere a fiecărui punct

Se poate observa că discul unității centrale este în general păstrat, deoarece este mapat la sine, dar fiecare punct (cu excepția zero) este acoperit de două ori, ceea ce face ca figura să fie confuză. De exemplu, punctele corespunzătoare $+1$ ${\ displaystyle +1}$ $+1$ (3:00 am) ea $-1$ ${\ displaystyle -1}$ $-1$ (9:00 am) sunt ambele trimise $+1$ ${\ displaystyle +1}$ $+1$ (la ora 3, în dreapta figurii, spre mijloc), $+i$ ${\ displaystyle + i}$ ${\ displaystyle + i}$ (12:00) e $-i$ ${\ displaystyle -i}$ ${\ displaystyle -i}$ (6:00 am) sunt ambele trimise $-1$ ${\ displaystyle -1}$ $-1$ (stânga în figură, spre mijloc).

Dacă vrem să avem de-a face cu o funcție injectivă, trebuie să restrângem domeniul transformării: putem, de exemplu, să ne restrângem la cazul semiplanului pozitiv sau al semiplanului negativ. Cifra rezultată nu va avea neclaritate din cauza suprapunerii.

Semiplanul negativ la pătrat

Semiplanul pozitiv la pătrat

Privind mai departe spre figură, estompările se estompează și obțineți același aspect, mare, pentru întreaga teselare.

Semiplanul negativ la pătrat.
Ceas pătrat: conform, dar nu injectiv.
Semiplanul pozitiv pătrat.

Imagine contra

Graficul salinității oceanului prezentat ca o imagine de contor

Pentru a obține o figură frumoasă conformă, este mai bine să lăsați în afara cartografierea directă și să luați în considerare figura obținută prin intermediul funcției inverse.

Cifra nu mai țiglă domeniul funcției ci codomainul acesteia (mai corect, dar cu un joc de cuvinte, ar trebui spus că „nu mai țiglă domeniul funcției ci imaginea domeniului ”). În această reprezentare, punctul $z$ ${\ displaystyle z}$ $z$ preia culoarea pixelului $f(z)$ ${\ displaystyle f (z)}$ $f (z)$ .

Imaginea contor a funcției

z\mapsto z^{2}

{\ displaystyle z \ mapsto z ^ {2}}

{\ displaystyle z \ mapsto z ^ {2}}

. Gradul

2

{\ displaystyle 2}

2

este dezvăluit prin duplicarea mâinilor

Rețineți duplicarea mâinilor și a numerelor de pe cadran: punctele $z$ ${\ displaystyle z}$ $z$ Și $-z$ ${\ displaystyle -z}$ ${\ displaystyle -z}$ sunt colorate la fel, deoarece ambele sunt mapate la același loc $z^{2}$ ${\ displaystyle z ^ {2}}$ ${\ displaystyle z ^ {2}}$ .

Un polinom de grad

4

{\ displaystyle 4}

4

. Observați zerourile derivatei sale. Zerourile simple nu au nimic special despre ele

Imaginea contra a

z\mapsto z^{3}

{\ displaystyle z \ mapsto z ^ {3}}

{\ displaystyle z \ mapsto z ^ {3}}

. Gradul 3 este dezvăluit prin triplarea acelor de ceas și a numerelor centrate pe origine

În mod similar, pentru ceea ce sa spus deja, monomiul de ordine k trimite k puncte diferite către același punct țintă.

Din imaginea contorului puteți obține o mulțime de informații utile despre harta conformă. Deoarece factorul de zoom al hărții directe este reprezentat de derivată, factorul de zoom de cartografiere inversă este reciproc al derivatei: unde harta directă mărește ( modulul factorului de scară mai mare $1$ ${\ displaystyle 1}$ $1$ ), harta inversă se micșorează ( modulul factorului de scală este mai mic decât $1$ ${\ displaystyle 1}$ $1$ ). Rezultă că de data aceasta se întâmplă ceva foarte special în corespondență cu zerourile derivatei funcției: factorul de zoom devine infinit, cu evidente deformări structurale puternice vizibile în apropierea acestor puncte. În plus, gradul de zero poate fi derivat cu ușurință din numărul de repetări ale caracteristicii de proiectare în jurul singularității (vezi mâinile, numerele de apel și literele din jur, toate acestea fiind dublate și triplate, respectiv, în imaginea contra $z\mapsto z^{2}$ ${\ displaystyle z \ mapsto z ^ {2}}$ ${\ displaystyle z \ mapsto z ^ {2}}$ Și $z\mapsto z^{3}$ ${\ displaystyle z \ mapsto z ^ {3}}$ ${\ displaystyle z \ mapsto z ^ {3}}$ ).

Puteți observa, de asemenea, când derivata este reală și pozitivă: există mărire, dar nu există rotație, iar figura este „în picioare”. Pe de altă parte, atunci când este real negativ, situația este similară, dar cifra este „pe dos”. Când ne restrângem la axa reală , ne putem imagina o reprezentare aproximativă a graficului unei funcții reale. Punctele de inflexiune vor fi, de asemenea, identificate: sunt situate la minimul și maximul factorului de zoom.

Inversie, poli

După funcțiile holomorfe, un alt exemplu de hărți holomorfe local este oferit de funcțiile meromorfe , dintre care este posibil să se identifice atât poziția, cât și ordinea polilor .

Inversiunea

z\mapsto 1/z

{\ displaystyle z \ mapsto 1 / z}

{\ displaystyle z \ mapsto 1 / z}

.

Inversiunea (vedere detaliată)

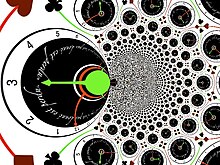
Să luăm în considerare funcția $z\mapsto 1/z$ ${\ displaystyle z \ mapsto 1 / z}$ ${\ displaystyle z \ mapsto 1 / z}$ , care are un pol simplu la zero. Este un caz special al transformării Möbius , adică o transformare de tip $z\mapsto {\frac {az+b}{cz+d}}$ ${\ displaystyle z \ mapsto {\ frac {az + b} {cz + d}}}$ ${\ displaystyle z \ mapsto {\ frac {az + b} {cz + d}}}$ , in care $la$ ${\ displaystyle a}$ $la$ , $b$ ${\ displaystyle b}$ $b$ , $c$ ${\ displaystyle c}$ $c$ Și $d$ ${\ displaystyle d}$ $d$ sunt patru numere complexe astfel încât $ad-bc\neq 0$ ${\ displaystyle ad-bc \ neq 0}$ ${\ displaystyle ad-bc \ neq 0}$ (în acest caz avem $a=d=0$ ${\ displaystyle a = d = 0}$ ${\ displaystyle a = d = 0}$ Și $b=c=1$ ${\ displaystyle b = c = 1}$ ${\ displaystyle b = c = 1}$ ). Prin urmare, trimite cercuri și linii în cercuri și linii, care este caracteristica sa principală. În special, liniile orizontale și verticale sunt transformate în cercuri care trec prin zero. Este foarte asemănător inversiunii circulare obișnuite ( $z\mapsto 1/{\bar {z}}$ ${\ displaystyle z \ mapsto 1 / {\ bar {z}}}$ ${\ displaystyle z \ mapsto 1 / {\ bar {z}}}$ ) și astfel face ca interiorul cercului unitar să „explodeze”, în interiorul căruia restul planului este „comprimat”. Schimbând linii curbe cu linii drepte și invers, transformarea se pretează la efecte grafice curioase: este utilizată pe scară largă de artiști pentru a obține deformări structurale anamorfice spectaculoase ale imaginilor.

Doi poli la

+{\frac {1}{2}}

{\ displaystyle + {\ frac {1} {2}}}

{\ displaystyle + {\ frac {1} {2}}}

Și

-{\frac {1}{2}}

{\ displaystyle - {\ frac {1} {2}}}

{\ displaystyle - {\ frac {1} {2}}}

Un pol al ordinii

2

{\ displaystyle 2}

2

pentru

z\mapsto 1/z^{2}

{\ displaystyle z \ mapsto 1 / z ^ {2}}

{\ displaystyle z \ mapsto 1 / z ^ {2}}

La fel ca zerourile, polii pot fi simpli sau de ordin superior. Cercurile, în general, sunt conservate doar la un nivel infinitesimal. Stâlpii de ordin superior pot fi vopsiți la fel de mulți stâlpi simpli la un loc.

Logaritm și exponențial

funcția exponențială

z\mapsto e^{z}

{\ displaystyle z \ mapsto e ^ {z}}

{\ displaystyle z \ mapsto e ^ {z}}

. Rețineți invarianțele în ceea ce privește omotitatea și rotația, corespunzătoare invarianțelor la translația orizontală (reală) și verticală (imaginară) în rețeaua țintă

Funcția logaritmică

z\mapsto \log(z)

{\ displaystyle z \ mapsto \ log (z)}

{\ displaystyle z \ mapsto \ log (z)}

. Observați, în stânga, benzile verticale, efectul „derulării” cercurilor și discurilor centrate pe origine. În schimb, observați mâinile roșii și verzi: liniile care ies din centru sunt transformate în linii orizontale

O transformare importantă în analiza și cartografia complexă este transformarea din coordonatele carteziene $(x,y)$ ${\ displaystyle (x, y)}$ $(X y)$ la coordonatele polare $(r,\theta )$ ${\ displaystyle (r, \ theta)}$ ${\ displaystyle (r, \ theta)}$ . Această transformare este exprimată de perechea de funcții logaritm / exponențiale una inversă a celeilalte ( $\log(\exp(z))=z$ ${\ displaystyle \ log (\ exp (z)) = z}$ ${\ displaystyle \ log (\ exp (z)) = z}$ ). În mod eficient,

$\log(r\,e^{i\theta })=\log(r)+i\theta$ ${\ displaystyle \ log (r \, e ^ {i \ theta}) = \ log (r) + i \ theta}$ ${\ displaystyle \ log (r \, e ^ {i \ theta}) = \ log (r) + i \ theta}$ trimite $(r,\theta )$ ${\ displaystyle (r, \ theta)}$ ${\ displaystyle (r, \ theta)}$ în $(x=log(r),y=\theta )$ ${\ displaystyle (x = log (r), y = \ theta)}$ ${\ displaystyle (x = log (r), y = \ theta)}$ Și $\exp(x+i\,y)=\exp(x)\,e^{i\,y}$ ${\ displaystyle \ exp (x + i \, y) = \ exp (x) \, e ^ {i \, y}}$ ${\ displaystyle \ exp (x + i \, y) = \ exp (x) \, e ^ {i \, y}}$ trimite $(x,y)$ ${\ displaystyle (x, y)}$ $(X y)$ în $(r=\exp(x),\theta =y)$ ${\ displaystyle (r = \ exp (x), \ theta = y)}$ ${\ displaystyle (r = \ exp (x), \ theta = y)}$ .

În figura obținută, logaritmul derulează cercurile centrate pe origine, transformându-le în linii verticale, în timp ce razele sunt transformate în linii orizontale: banda verde mare verticală este pivotul circular al mâinii în timp ce interiorul cadranului este transformat în banda verticală neagră traversată de scrierea verticală în franceză ; mâinile verzi și roșii, pe de altă parte, care sunt drepte din centru, sunt transformate în linii orizontale.

Comportamentul exponențialului este în schimb opusul: înfășoară liniile verticale transformându-le în cercuri concentrice și trimite linii drepte orizontale în raze care ies din origine.

Rețineți că logaritmul tinde spre infinit pe măsură ce se apropie de zero, dar mult mai lent decât inversiunea.

Singularități esențiale

Singularitatea esențială :

z\mapsto e^{1/z}

{\ displaystyle z \ mapsto e ^ {1 / z}}

{\ displaystyle z \ mapsto e ^ {1 / z}}

.

Funcțiile analitice prezintă un alt tip de singularitate, de exemplu singularitatea esențială .

$z\mapsto e^{1/z}$ ${\ displaystyle z \ mapsto e ^ {1 / z}}$ ${\ displaystyle z \ mapsto e ^ {1 / z}}$ este zero pentru $z\to 0^{-}$ ${\ displaystyle z \ to 0 ^ {-}}$ ${\ displaystyle z \ to 0 ^ {-}}$ ,

cu o acumulare de zerouri,

și nedeterminat pentru $z\to 0^{+}$ ${\ displaystyle z \ to 0 ^ {+}}$ ${\ displaystyle z \ to 0 ^ {+}}$ , cu o acumulare de poli.

Raza de convergență

Funcțiile analitice sunt (local) reprezentabile ca sume de serii de putere . Având în vedere un punct, seria Taylor admite o rază de convergență . Comparația dintre imaginea contra funcției și seria Taylor a acesteia trunchiată până la o anumită ordine, ne permite să ilustrăm conceptul:

Funcția tangentă are câte un pol simplu ${\frac {k\pi }{2}}$ ${\ displaystyle {\ frac {k \ pi} {2}}}$ ${\ displaystyle {\ frac {k \ pi} {2}}}$ . Prezintă o singularitate esențială până la infinit.
Trunchierea la comandă $7$ ${\ displaystyle 7}$ ${\ displaystyle 7}$ din seria sa Taylor în jurul valorii 0 oferă o bună aproximare în cadrul discului de convergență .

Notă

^ ( FR ) Christian Mercat, «Applications conformes» , Images des mathématiques , CNRS , Université Claude Bernard, Lyon 1, 2009
^ " Ce qui n'est pas donné est perdu " ("ceea ce nu este dat se pierde", o afirmație uneori atribuită Maicii Tereza din Calcutta )

Bibliografie

( FR ) Christian Mercat, «Applications conformes» , Images des mathématiques , CNRS , Université Claude Bernard, Lyon 1, 2009.

Lecturi suplimentare

( FR ) Michèle Audin, Analyze complexe , Université Louis Pasteur , Strasbourg .
( EN ) Tristan Needham , Visual Complex Analysis , Oxford University Press , 1999 ISBN 0-19-853446-9 .

Elemente conexe

linkuri externe

Imaginile articolului au fost obținute folosind acest applet Java , din care este disponibilă o versiune diferită pentru macOS care este capabilă să deformeze într-un mod amuzant fluxul video care vine de la camera web ( java -d32 -jar ComplexMap.jar ). Folosește biblioteca JTEM- Java Tools for Experimental Mathematics din Technische Universität Berlin
Modul de cartografiere conformă de John H. Mathews
Vizualizare interactivă a diferitelor hărți conforme , pe virtualmathmuseum.org . Adus pe 2 ianuarie 2012 (arhivat din original la 8 februarie 2016) .
Applet Java pentru afișarea hărților conforme
Conformal Maps de Michael Trott, Wolfram Demonstrations Project .
Applet Java ^{[ link rupt ]} de Jürgen Richter-Gebert, obținut cu Cenușăreasa .
(EN) Steven Lehar, Geometric Algebra: Conformal Geometry , slehar pe 24 iulie 2014. Adus pe 11 ianuarie 2017.

Portal de artă

Portalul de matematică

[1] ( FR ) Christian Mercat, «Applications conformes» , Images des mathématiques , CNRS , Université Claude Bernard, Lyon 1, 2009

[2] " Ce qui n'est pas donné est perdu " ("ceea ce nu este dat se pierde", o afirmație uneori atribuită Maicii Tereza din Calcutta )

[1]

[2]