Lista politopilor obișnuiți

Această intrare listează politopii obișnuiți în spațiile euclidiene , sferice și hiperbolice . Notația lui Schläfli descrie fiecare politop obișnuit și este folosită extensiv mai jos ca abreviere pentru fiecare dintre ele.

Politopii obișnuiți sunt grupați după mărime și împărțiți în forme convexe, neconvexe și infinite. Formele neconvexe utilizează aceleași vârfuri ca formele convexe, dar au fațete intersectate. Formele infinite teselează un spațiu euclidian cu o dimensiune inferioară.

Formele infinite pot fi extinse pentru a tessela un spațiu hiperbolic . Spațiul hiperbolic este ca spațiul normal pe distanțe scurte, dar liniile paralele diverg pe distanțe mari. Acest lucru permite figurilor de vârf să aibă un defect negativ al unghiului , cum ar fi compunerea unui vârf de 7 triunghiuri echilaterale și să le permită să se întindă în același plan. Nu se poate face pe planul regulat, dar la scara corectă se poate face pe planul hiperbolic.

Lista politopilor obișnuiți sortată după mărime

Dimensiune	Convex	Nu convex	Teselări Euclidian convex	Teselări hiperbolic convex	Teselări hiperbolic nu convex
2	∞ poligoane	∞ poligoane stelare	1	1	0
3	5 solide platonice	4 solide Kepler-Poinsot	3 teselări	∞	∞
4	6 policore convexe	10 policore ale lui Schläfli-Hess	1 stupi	4	0
5	3 politopi 5-conveși	0 5-politopi neconveși	3 teselări	5	4
6+	3	0	1	0	0

Politopi bidimensionali obișnuiți

Politopii bidimensionali se numesc poligoane . Poligoanele regulate sunt echilaterale și ciclice .

De obicei, numai poligoanele convexe sunt considerate regulate, totuși poligoanele stelare , cum ar fi pentagrama , pot fi, de asemenea, considerate regulate. Folosesc aceleași vârfuri ca formele convexe, dar se conectează într-o cale alternativă care merge de câteva ori înainte de a reveni la punctul de plecare.

Poligoanele stelare ar trebui să fie numite non-convexe, mai degrabă decât concave, deoarece marginile care se intersectează nu generează vârfuri noi și toate vârfurile sunt pe o circumferință.

Politopi tridimensionali regulari

În 3 dimensiuni, politopii obișnuiți se numesc poliedre :

Un poliedru regulat cu simbolul Schläfli $\{p,q\}$ ${\ displaystyle \ {p, q \}}$ ${\ displaystyle \ {p, q \}}$ are fețe de tip regulat $\{p\}$ ${\ displaystyle \ {p \}}$ ${\ displaystyle \ {p \}}$ , și figura de sus regulată $\{q\}$ ${\ displaystyle \ {q \}}$ ${\ displaystyle \ {q \}}$ .

O figură la vârf (a unui poliedru) este un poligon, care poate fi obținut prin conectarea acelor vârfuri care se află la o margine distanță de un vârf dat. Pentru poliedre regulate, această figură de vârf este întotdeauna un poligon regulat (și plan).

Existența unui poliedru regulat $\{p,q\}$ ${\ displaystyle \ {p, q \}}$ ${\ displaystyle \ {p, q \}}$ este constrâns de o inegalitate, legată de unghiul de defect al figurii de la vârf:

1/p+1/q>1/2

{\ displaystyle 1 / p + 1 / q> 1/2}

{\ displaystyle 1 / p + 1 / q> 1/2}

: Poliedru (existent în spațiul euclidian tridimensional)

1/p+1/q=1/2

{\ displaystyle 1 / p + 1 / q = 1/2}

{\ displaystyle 1 / p + 1 / q = 1/2}

: Teselare plană euclidiană

1/p+1/q<1/2

{\ displaystyle 1 / p + 1 / q <1/2}

{\ displaystyle 1 / p + 1 / q <1/2}

: Teselarea planului hiperbolic

Numărând permutațiile , găsim 5 forme convexe, 4 forme neconvexe și 3 teselări plane, toate cu poligoane $\{p\}$ ${\ displaystyle \ {p \}}$ ${\ displaystyle \ {p \}}$ Și $\{q\}$ ${\ displaystyle \ {q \}}$ ${\ displaystyle \ {q \}}$ limitat la: $\{3\},\{4\},\{5\}$ ${\ displaystyle \ {3 \}, \ {4 \}, \ {5 \}}$ ${\ displaystyle \ {3 \}, \ {4 \}, \ {5 \}}$ , {5/2} și $\{6\}$ ${\ displaystyle \ {6 \}}$ ${\ displaystyle \ {6 \}}$ .

În plus față de spațiul euclidian, există un set infinit de teselări regulate ale planului hiperbolic.

Politopi reguli cu patru dimensiuni

Policorurile obișnuite cu simbolul Schläfli $\{p,q,r\}$ ${\ displaystyle \ {p, q, r \}}$ ${\ displaystyle \ {p, q, r \}}$ au celule tip $\{p,q\}$ ${\ displaystyle \ {p, q \}}$ ${\ displaystyle \ {p, q \}}$ , tastați fețele $\{p\}$ ${\ displaystyle \ {p \}}$ ${\ displaystyle \ {p \}}$ , figuri de margine $\{r\}$ ${\ displaystyle \ {r \}}$ ${\ displaystyle \ {r \}}$ , și figuri de top $\{q,r\}$ ${\ displaystyle \ {q, r \}}$ ${\ displaystyle \ {q, r \}}$ .

O figură la vârf (a unui policor) este un poliedru, care poate fi obținut din dispunerea vârfurilor apropiate de un vârf dat. Pentru un policor regulat, această figură de vârf este un poliedru regulat.
O figură de margine este un poligon, obținut prin aranjarea fețelor în jurul unei margini. Pentru policore obișnuite, această figură de margine este un poligon regulat.

Existența unui policor regulat $\{p,q,r\}$ ${\ displaystyle \ {p, q, r \}}$ ${\ displaystyle \ {p, q, r \}}$ este legat de existența poliedrelor regulate $\{p,q\},\{q,r\}$ ${\ displaystyle \ {p, q \}, \ {q, r \}}$ ${\ displaystyle \ {p, q \}, \ {q, r \}}$ .

Fiecare dintre acestea va exista într-un spațiu dependent de următoarea expresie:

\sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)

{\ displaystyle \ sin \ left ({\ frac {\ pi} {p}} \ right) \ sin \ left ({\ frac {\ pi} {r}} \ right) - \ cos \ left ({\ frac {\ pi} {q}} \ right)}

{\ displaystyle \ sin \ left ({\ frac {\ pi} {p}} \ right) \ sin \ left ({\ frac {\ pi} {r}} \ right) - \ cos \ left ({\ frac {\ pi} {q}} \ right)}

>0

{\ displaystyle> 0}

{\ displaystyle> 0}

: Policor de suprafață hipersferică (în spațiu cu patru dimensiuni)

=0

{\ displaystyle = 0}

{\ displaystyle = 0}

: Stup stup euclidian

<0

{\ displaystyle <0}

{\ displaystyle <0}

: Stup hiperbolic tridimensional

Aceste constrângeri permit 21 de forme: 6 sunt convexe, 10 sunt neconvexe, 1 este un stup euclidian tridimensional și 4 sunt stupi hiperbolici.

Caracteristica lui Euler $\chi$ ${\ displaystyle \ chi}$ $\care$ pentru polycoris este: $\chi =V+F-E-C$ ${\ displaystyle \ chi = V + FEC}$ ${\ displaystyle \ chi = V + F-E-C}$ și este 0 pentru toate formele.

Politopi în cinci dimensiuni regulate

În cinci dimensiuni , un politop regulat poate fi scris ca $\{p,q,r,s\}$ ${\ displaystyle \ {p, q, r, s \}}$ ${\ displaystyle \ {p, q, r, s \}}$ unde este $\{p,q,r\}$ ${\ displaystyle \ {p, q, r \}}$ ${\ displaystyle \ {p, q, r \}}$ este tipul de hipercelula, $\{p,q\}$ ${\ displaystyle \ {p, q \}}$ ${\ displaystyle \ {p, q \}}$ este tipul de celulă, $\{p\}$ ${\ displaystyle \ {p \}}$ ${\ displaystyle \ {p \}}$ este tipul feței și $\{s\}$ ${\ displaystyle \ {s \}}$ ${\ displaystyle \ {s \}}$ este figura din față, $\{r,s\}$ ${\ displaystyle \ {r, s \}}$ ${\ displaystyle \ {r, s \}}$ este figura din colț și $\{q,r,s\}$ ${\ displaystyle \ {q, r, s \}}$ ${\ displaystyle \ {q, r, s \}}$ este figura din partea de sus.

Un politop 5 se numește politomer și, dacă infinit (adică un stup ), un politop 5 poate fi numit

O figură la vârf (a unui 5-politop) este un policor, care poate fi obținut din dispunerea vârfurilor aproape de un vârf dat.

O figură de margine (a unui 5-politop) este un poliedru, care poate fi obținut prin aranjarea fețelor în jurul unei muchii date.

O figură a feței (a unui 5-politop) este un poligon, care poate fi obținut prin aranjarea celulelor în jurul unei fețe date.

Un politop obișnuit $\{p,q,r,s\}$ ${\ displaystyle \ {p, q, r, s \}}$ ${\ displaystyle \ {p, q, r, s \}}$ există doar dacă $\{p,q,r\}$ ${\ displaystyle \ {p, q, r \}}$ ${\ displaystyle \ {p, q, r \}}$ Și $\{q,r,s\}$ ${\ displaystyle \ {q, r, s \}}$ ${\ displaystyle \ {q, r, s \}}$ sunt policrom regulat.

Spațiul pe care îl umple se bazează pe următoarea expresie:

{\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}

{\ displaystyle {\ frac {\ cos ^ {2} \ left ({\ frac {\ pi} {q}} \ right)} {\ sin ^ {2} \ left ({\ frac {\ pi} {p }} \ right)}} + {\ frac {\ cos ^ {2} \ left ({\ frac {\ pi} {r}} \ right)} {\ sin ^ {2} \ left ({\ frac { \ pi} {s}} \ right)}}}

{\ displaystyle {\ frac {\ cos ^ {2} \ left ({\ frac {\ pi} {q}} \ right)} {\ sin ^ {2} \ left ({\ frac {\ pi} {p }} \ right)}} + {\ frac {\ cos ^ {2} \ left ({\ frac {\ pi} {r}} \ right)} {\ sin ^ {2} \ left ({\ frac { \ pi} {s}} \ right)}}}

<1

{\ displaystyle <1}

{\ displaystyle <1}

: Politop sferic

=1

{\ displaystyle = 1}

{\ displaystyle = 1}

: Teselarea spațiului euclidian cu patru dimensiuni

>1

{\ displaystyle> 1}

{\ displaystyle> 1}

: Teselarea spațiului hiperbolic în patru dimensiuni

Cu aceste constrângeri obținem 3 politopi conveși, zero politopi neconveși, 3 teselări ale spațiului euclidian cu patru dimensiuni și 5 teselări ale spațiului hiperbolic cu patru dimensiuni.

Politopi clasici conveși

Două dimensiuni

Simbolul lui Schläfli ${p}$ ${\ displaystyle {p}}$ ${\ displaystyle {p}}$ reprezintă un p -agon regulat.

Poligoanele regulate convexe sunt:

Nume	Schläfli Simbol {p}
triunghi echilateral	{3}
pătrat	{4}
pentagon regulat	{5}
hexagon regulat	{6}
heptagon regulat	{7}
octogon regulat	{8}
nonagon regulat	{9}
decagon regulat	{10}
endecagon regulat	{11}
dodecagon regulat	{12}
... n- agono regulat	{ n }
stup de albine	{ ∞ }

{2}	{3}	{4}	{5}	{6}	{7}	{8}	{9}	{10}	{11}	{12}

Un digon , {2}, poate fi considerat un poligon regulat degenerat.

Trei dimensiuni

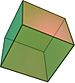
Cele cinci poliedre regulate convexe se numesc solide platonice . (Pentru fiecare vârf este dată figura de la vârful corespunzător.)

Nume	Simbolul Schläfli {p, q}	Fețe {p}	Margini	Vârfuri {q}	χ	Simetrie	Dual
Tetraedru	{3.3}	4 {3}	6	4 {3}	2	T _d	Auto-modulant
Cub (hexaedru)	{4.3}	6 {4}	12	8 {3}	2	O _h	Octaedru
Octaedru	{3.4}	8 {3}	12	6 {4}	2	O _h	cub
Dodecaedru	{5.3}	12 {5}	30	20 {3}	2	Eu _h	Icosaedru
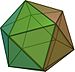
Icosaedru	{3.5}	20 {3}	30	12 {5}	2	Eu _h	Dodecaedru

{3.3}	{4.3}	{3.4}	{5.3}	{3.5}

În geometria sferică , osoedrul (simbolul Schläfli {2, n}) și diedrul (simbolul Schläfli {n, 2}) pot fi considerate poliedre regulate ( teselări ale sferei ).

Patru dimensiuni

Cele 6 policorize obișnuite sunt după cum urmează:

Nume	Simbolul Schläfli {p, q, r}	Celulele {p, q}	Fețe {p}	Margini {r}	Vârfuri {q, r}	Dual {r, q, p}
5-celule (Pentacor)	{3,3,3}	5 {3.3}	10 {3}	10 {3}	5 {3.3}	Auto-modulant
8-celule (Hypercube)	{4,3,3}	8 {4.3}	24 {4}	32 {3}	16 {3.3}	16-celule
16-celule	{3,3,4}	16 {3.3}	32 {3}	24 {4}	8 {3.4}	Hipercub
24 de celule	{3,4,3}	24 {3.4}	96 {3}	96 {3}	24 {4.3}	Auto-modulant
120 de celule	{5,3,3}	120 {5.3}	720 {5}	1200 {3}	600 {3.3}	600 de celule
600 de celule	{3,3,5}	600 {3.3}	1200 {3}	720 {5}	120 {3.5}	120 de celule

5-celule	8-celule	16-celule	24 de celule	120 de celule	600 de celule
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Proiecții ortografice cu zăbrele

Proiecții ortografice solide (centrate în celule)
Plic tetraedrică	Plic cub	Plic octaedrică	Plic cubocatedrică	Plic de triacontahedron trombat rombic	Plic pentacisdodecaedric
Diagrame Lattice Schlegel ( proiecție în perspectivă )
(centrat în celulă)	(centrat în celulă)	(centrat în celulă)	(centrat în celulă)	(centrat în celulă)	(centrat în vârf)
Proiecții stereografice reticulare (hipersferice)

Politopi finiti neconvexe - politopi stelati

Două dimensiuni

Există politopi reguli neconveși bidimensionali infini, ale căror simboluri Schläfli constau din numere raționale {m / n}. Se numesc poligoane stelare .

În general, pentru orice număr natural n, există poligoane stelate cu n-puncte cu simboluri Schläfli {n / m} pentru fiecare m, astfel încât m <n / 2 (sau echivalent {n / m} = {n / (nm)} ) em și n sunt coprimă .

Nume	Simbolul Schläfli {n / m}
personal	{5/2}
heptagrama	{7/2}, {7/3}
octagramă	{8/3}
eneagramă	{9/2}, {9/4}
decagram	{10/3}
hendecagramă	{11/2} {11/3}, {11/4}, {11/5}
dodecagramă	{12/5}
... n-agramele	{ n / m }

{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}

Dimensiuni superioare

Nu există politopi neconveși în cinci sau mai multe dimensiuni.

Teselări

Beirotopi

Un apeirotop este, ca orice alt politop, o hipersuprafață nelimitată. Diferența este că, în timp ce hipersuprafața unui politop se curbează în jurul său pentru a cuprinde un volum finit de hiperspațiu, un apeirotop pur și simplu nu se oprește niciodată.

Unii consideră apeirotopii pur și simplu ca un anumit tip de politop, în timp ce alții îi consideră a fi dintr-o specie complet diferită.

Politopi abstracte

Bibliografie

Coxeter , politopi obișnuiți , al treilea. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabelele I și II: politopi obișnuiți și faguri de miere, pp. 294–296)
Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999 ISBN 0-486-40919-8 (Capitolul 10: Faguri regulate în spațiul hiperbolic, tabele rezumative II, III, IV, V, p212-213)

Elemente conexe

Poligon
- Poligon regulat
- Poligon stelar
Poliedru
- Poliedru regulat (cele 5 solide platonice regulate și cele 4 solide Kepler-Poinsot )
  - Poliedru uniform
Policoro (matematică)
- Policore regulate convexe (6 policore obișnuite)
  - Policor uniform
- Policlor din Schläfli-Hess (10 policoruri înstelate obișnuite)
Teselări
- Suprapunerea poligoanelor obișnuite
- Stupi convex uniformi
Politop regulat
- Politop uniform

linkuri externe

Solidele platonice , pe math.utah.edu .
Poliedrele Kepler-Poinsot , pe georgehart.com .
Dezvoltări de politopi reguli în patru dimensiuni , pe weimholt.com . Adus la 29 septembrie 2007 (arhivat din original la 17 iulie 2011) .
Glosar multidimensional (vezi Hexacosichoron și Hecatonicosachoron )
Vizualizator de politopi , pe geocities.com .
Politopi și gruparea optimă a punctelor p în sfere n-dimensionale , pe presh.com . Adus la 29 septembrie 2007 (arhivat din original la 15 iunie 2006) .
Un atlas de politopi mici și reguli , pe abstract-polytopes.com .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică