Spațiul hiperbolic

O teselare a planului hiperbolic folosind triunghiuri.

În matematică , spațiul hiperbolic este un spațiu introdus independent de matematicienii Bolyai și Lobachevsky în secolul al XIX-lea , pe care este definită o anumită geometrie neeuclidiană , numită geometrie hiperbolică . Acesta este cel mai important exemplu de geometrie neeuclidiană, împreună cu geometria eliptică .

Spațiul hiperbolic are o dimensiune arbitrară $n$ ${\ displaystyle n}$ $n$ și este indicat cu $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ . Poate fi realizat prin diferite modele echivalente, precum discul , jumătatea spațiului Poincaré sau modelul hiperboloid . La fel ca în geometria euclidiană , cele mai studiate spații sunt planul hiperbolic $\mathbb {H} ^{2}$ ${\ displaystyle \ mathbb {H} ^ {2}}$ ${\ displaystyle \ mathbb {H} ^ {2}}$ și spațiul hiperbolic tridimensional $\mathbb {H} ^{3}$ ${\ displaystyle \ mathbb {H} ^ {3}}$ ${\ mathbb H} ^ {3}$ .

Modelele

Spațiul hiperbolic $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este un spațiu particular, pe care este definită o geometrie care satisface primele 4 axiome ale lui Euclid, dar nu și a cincea . Geometria prezentă în acest spațiu se numește hiperbolică .

Numarul $n$ ${\ displaystyle n}$ $n$ indică dimensiunea spațiului hiperbolic. În fiecare dimensiune $n$ ${\ displaystyle n}$ $n$ , spațiul hiperbolic poate fi realizat de diferite modele , toate echivalente.

Model de disc

Același subiect în detaliu: discul Poincaré .

Trei linii incidente în modelul discului. O linie este un arc de circumferință (sau segment) ortogonal față de margine.

În modelul discului Poincaré , spațiul hiperbolic este mingea $n$ ${\ displaystyle n}$ $n$ -dimensional

B^{n}=\{x\in \mathbb {R} ^{n}\ |\ |x|<1\}.

{\ displaystyle B ^ {n} = \ {x \ in \ mathbb {R} ^ {n} \ | \ | x | <1 \}.}

{\ displaystyle B ^ {n} = \ {x \ in \ mathbb {R} ^ {n} \ | \ | x | <1 \}.}

Pentru $n=2$ ${\ displaystyle n = 2}$ $n = 2$ , acesta este cercul razei unitare centrat în originea planului cartezian , fără circumferința muchiei.

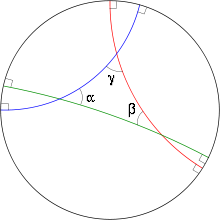
O linie din discul Poincaré este un arc de circumferință sau un segment care intersectează marginea $\partial B^{n}$ ${\ displaystyle \ partial B ^ {n}}$ ${\ displaystyle \ partial B ^ {n}}$ a mingii $B^{n}$ ${\ displaystyle B ^ {n}}$ ${\ displaystyle B ^ {n}}$ ortogonal în două puncte. Două „linii” care se intersectează într-un punct formează un unghi , iar lățimea acestuia este egală cu unghiul format de tangente.

Model pe jumătate de spațiu

Același subiect în detaliu: jumătatea spațiului Poincaré .

În modelul Poincaré al jumătății de spațiu, spațiul hiperbolic este jumătatea de spațiu

\{(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}\ |\ x_{n}>0\}.

{\ displaystyle \ {(x_ {1}, \ ldots, x_ {n}) \ in \ mathbb {R} ^ {n} \ | \ x_ {n}> 0 \}.}

{\ displaystyle \ {(x_ {1}, \ ldots, x_ {n}) \ in \ mathbb {R} ^ {n} \ | \ x_ {n}> 0 \}.}

Ca și în modelul de disc, liniile hiperbolice sunt arcele de circumferință și liniile ortogonale la margine. În acest model, marginea este hiperplanul orizontal $x_{n}=0$ ${\ displaystyle x_ {n} = 0}$ ${\ displaystyle x_ {n} = 0}$ .

Modelul Klein

Același subiect în detaliu: modelul Klein .

V postulatul geometriei hiperbolice în modelul Klein.

În modelul Klein spațiul hiperbolic este (la fel ca în modelul discului) setul de puncte din interiorul unui cerc $C.$ ${\ displaystyle C}$ $C.$ . Liniile drepte, totuși, sunt segmente reale: simplitatea mai mare în descrierea liniilor drepte este plătită în descrierea unghiurilor, care sunt distorsionate în raport cu unghiurile euclidiene: unghiul format din două linii drepte nu este cel euclidian. , dar depinde de aceasta printr-o formulă adecvată.

Distanța dintre două puncte $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ intern discului este

d(P,Q)={\frac {1}{2}}\log {\frac {|Q-A||P-B|}{|P-A||Q-B|}}

{\ displaystyle d (P, Q) = {\ frac {1} {2}} \ log {\ frac {| QA || PB |} {| PA || QB |}}}

{\ displaystyle d (P, Q) = {\ frac {1} {2}} \ log {\ frac {| Q-A || P-B |} {| P-A || Q-B |}}}

unde este $|R-S|$ ${\ displaystyle | RS |}$ ${\ displaystyle | R-S |}$ este distanța euclidiană între puncte $R.$ ${\ displaystyle R}$ $R.$ Și $S.$ ${\ displaystyle S}$ $S.$ . Punctele $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ sunt intersecțiile dintre linia euclidiană care trece $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ iar marginea $\partial B^{n}$ ${\ displaystyle \ partial B ^ {n}}$ ${\ displaystyle \ partial B ^ {n}}$ . Logaritmul este logaritmul natural . Argumentul logaritmului este raportul transversal al celor patru puncte aliniate.

Modelul hiperboloidului

În modelul hiperboloid , spațiul hiperbolic este hiperboloidul

H={\big \{}(x_{1},\ldots ,x_{n+1})\in \mathbb {R} ^{n+1}\ {\big |}\ x_{1}^{2}+\ldots +x_{n}^{2}-x_{n+1}^{2}=-1,x_{n+1}>0{\big \}}.

{\ displaystyle H = {\ big \ {} (x_ {1}, \ ldots, x_ {n + 1}) \ in \ mathbb {R} ^ {n + 1} \ {\ big |} \ x_ {1 } ^ {2} + \ ldots + x_ {n} ^ {2} -x_ {n + 1} ^ {2} = - 1, x_ {n + 1}> 0 {\ big \}}.}

{\ displaystyle H = {\ big \ {} (x_ {1}, \ ldots, x_ {n + 1}) \ in \ mathbb {R} ^ {n + 1} \ {\ big |} \ x_ {1 } ^ {2} + \ ldots + x_ {n} ^ {2} -x_ {n + 1} ^ {2} = - 1, x_ {n + 1}> 0 {\ big \}}.}

În acest model, o linie este dată de intersecția dintre $H.$ ${\ displaystyle H}$ $H.$ cu un avion care trece prin originea $\mathbb {R} ^{n+1}$ ${\ displaystyle \ mathbb {R} ^ {n + 1}}$ $\ mathbb {R} ^ {{n + 1}}$ . În acest context, este util să se definească su $\mathbb {R} ^{n+1}$ ${\ displaystyle \ mathbb {R} ^ {n + 1}}$ $\ mathbb {R} ^ {{n + 1}}$ o structură spațiu-timp Minkowski , adică produsul scalar cu semnătură $(n,1)$ ${\ displaystyle (n, 1)}$ ${\ displaystyle (n, 1)}$ :

\phi {\big (}(x_{1},\ldots ,x_{n+1}),(y_{1},\ldots ,y_{n+1}){\big )}=x_{1}y_{1}+\ldots +x_{n}y_{n}-x_{n+1}y_{n+1}.

{\ displaystyle \ phi {\ big (} (x_ {1}, \ ldots, x_ {n + 1}), (y_ {1}, \ ldots, y_ {n + 1}) {\ big)} = x_ {1} y_ {1} + \ ldots + x_ {n} y_ {n} -x_ {n + 1} y_ {n + 1}.}

{\ displaystyle \ phi {\ big (} (x_ {1}, \ ldots, x_ {n + 1}), (y_ {1}, \ ldots, y_ {n + 1}) {\ big)} = x_ {1} y_ {1} + \ ldots + x_ {n} y_ {n} -x_ {n + 1} y_ {n + 1}.}

Setul de $X$ ${\ displaystyle x}$ $X$ având $\phi (x,x)=-1$ ${\ displaystyle \ phi (x, x) = - 1}$ ${\ displaystyle \ phi (x, x) = - 1}$ are două componente conectate , dintre care una (cea superioară, având $x_{n+1}>0$ ${\ displaystyle x_ {n + 1}> 0}$ ${\ displaystyle x_ {n + 1}> 0}$ ) este hiperboloidul $H.$ ${\ displaystyle H}$ $H.$ . Distanța dintre două puncte $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ pe $H.$ ${\ displaystyle H}$ $H.$ este definit ca

d(P,Q)=\operatorname {arcosh} (\phi (P,Q)).

{\ displaystyle d (P, Q) = \ operatorname {arcosh} (\ phi (P, Q)).}

{\ displaystyle d (P, Q) = \ operatorname {arcosh} (\ phi (P, Q)).}

Definiție unică

Cea mai riguroasă definiție a spațiului hiperbolic $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este următorul: $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este singura varietate hiperbolică completă și pur și simplu conectată a dimensiunii $n$ ${\ displaystyle n}$ $n$ . O varietate hiperbolică este o varietate riemanniană având o curbură secțională constantă $-1$ ${\ displaystyle -1}$ $-1$ .

Prin „unic” înțelegem „până la izometrii ”: toate modelele enumerate mai sus sunt de fapt conectate prin izometrii, deci definesc în mod concret același soi. Faptul că există un singur spațiu cu aceste proprietăți este o teoremă importantă în geometria diferențială .

Subspatii

Geodezie

Geodezica este analogul liniei drepte în contextul euclidian. În modelul pe disc sau pe jumătate de spațiu, geodezicele sunt arcuri de circumferință sau linie dreaptă ortogonală la margine (a discului sau a jumătății de spațiu). Geodezica are proprietăți similare cu liniile din geometria euclidiană:

Pentru fiecare pereche de puncte distincte trece doar o singură dată geodezică,
Pentru fiecare punct și pentru fiecare vector tangent din punct, există o geodezică unică care trece prin punct și tangentă la acest vector,
Geodezica care leagă două puncte $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ este curba cu cea mai scurtă lungime dintre toate curbele care leagă cele două puncte. Această lungime este egală cu distanța $d(P,Q)$ ${\ displaystyle d (P, Q)}$ ${\ displaystyle d (P, Q)}$ .

Ultimele două proprietăți sunt valabile, cel puțin local, în fiecare varietate riemanniană .

Subspatii

Ca și în spațiul euclidian, în spațiul hiperbolic, pe lângă geodezice, sunt definite spații cu dimensiuni superioare, cum ar fi planurile.

Un subspatiu al $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este un subset $S.$ ${\ displaystyle S}$ $S.$ astfel încât pentru fiecare cuplu $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ de puncte în $S.$ ${\ displaystyle S}$ $S.$ întreaga trecere geodezică $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ este cuprins în $S.$ ${\ displaystyle S}$ $S.$ .

În timp ce geodezica există (cel puțin local) în fiecare soi riemannian, subspaiile există doar în soiuri foarte particulare, cum ar fi spațiul euclidian și hiperbolic. La fel ca în cazul euclidian, un subspatiu al $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ se dovedește a fi izometrică a $\mathbb {H} ^{k}$ ${\ displaystyle \ mathbb {H} ^ {k}}$ ${\ displaystyle \ mathbb {H} ^ {k}}$ , pentru unii $k$ ${\ displaystyle k}$ $k$ . Numarul $k$ ${\ displaystyle k}$ $k$ este dimensiunea subspațiului: pentru $k=1$ ${\ displaystyle k = 1}$ $k = 1$ primești un geodezic, pentru $k=2$ ${\ displaystyle k = 2}$ $k = 2$ un plan etc.

Intersecția a două subspatii este întotdeauna un subspatiu.

Paralelism

Același subiect în detaliu: Paralelismul în geometria hiperbolică .

Spațiul hiperbolic, însă, diferă clar de cel euclidian în noțiunea de paralelism . Având două subspatii $S.$ ${\ displaystyle S}$ $S.$ Și ${S.}^{'}$ ${\ displaystyle S '}$ $da$ disjunct, există două noțiuni distincte de paralelism:

Daca este o $k>0$ ${\ displaystyle k> 0}$ $k> 0$ astfel încât $d(x,x')>k$ ${\ displaystyle d (x, x ')> k}$ ${\ displaystyle d (x, x ')> k}$ pentru fiecare $X$ ${\ displaystyle x}$ $X$ în $S.$ ${\ displaystyle S}$ $S.$ și fiecare $X^{'}$ ${\ displaystyle x '}$ $X '$ în ${S.}^{'}$ ${\ displaystyle S '}$ $da$ , atunci cele două spații sunt ultraparalele .
Dacă nu există așa ceva $k$ ${\ displaystyle k}$ $k$ , cele două spații sunt asimptotic paralele .

În al doilea caz, există secvențe de puncte $(x_{i})$ ${\ displaystyle (x_ {i})}$ $(x_ {i})$ Și $(x_{i}')$ ${\ displaystyle (x_ {i} ')}$ ${\ displaystyle (x_ {i} ')}$ în $S.$ ${\ displaystyle S}$ $S.$ Și ${S.}^{'}$ ${\ displaystyle S '}$ $da$ ale cărei distanțe $d(x_{i},x_{i}')$ ${\ displaystyle d (x_ {i}, x_ {i} ')}$ ${\ displaystyle d (x_ {i}, x_ {i} ')}$ tind spre zero. Acest fenomen nu se produce în spațiile euclidiene.

Izometrii

Același subiect în detaliu: Izometria spațiului hiperbolic .

O izometrie a $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este o mișcare rigidă a spațiului, adică o funcție care mișcă toate punctele din spațiu menținând în același timp distanțele dintre ele. Izometriile spațiului hiperbolic se comportă în multe feluri similare cu cele din spațiul euclidian . Ele pot fi, de asemenea, studiate eficient prin sfera infinitului .

Spațiu omogen și izotrop

În spațiul euclidian $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ Exemple de izometrii sunt translațiile și rotațiile . Prin aceste izometrii este posibil să deplasăm puncte și linii după bunul plac: aceeași proprietate este valabilă și în spațiul hiperbolic: aceasta este de fapt omogenă și izotropă : punctele și liniile sunt toate nedistinguibile . Mai exact, pentru fiecare pereche de puncte $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ , și pentru fiecare pereche de linii $r$ ${\ displaystyle r}$ $r$ Și $s$ ${\ displaystyle s}$ $s$ trecători respectiv pentru $P.$ ${\ displaystyle P}$ $P.$ Și $Î$ ${\ displaystyle Q}$ $Î$ , există o izometrie a spațiului pe care îl trimite $P.$ ${\ displaystyle P}$ $P.$ în $Î$ ${\ displaystyle Q}$ $Î$ Și $r$ ${\ displaystyle r}$ $r$ în $s$ ${\ displaystyle s}$ $s$ .

Sferă până la infinit

În modelul discului Poincaré $B^{n}$ ${\ displaystyle B ^ {n}}$ ${\ displaystyle B ^ {n}}$ , sfera la infinitul spațiului hiperbolic $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ este marginea $\partial B^{n}$ ${\ displaystyle \ partial B ^ {n}}$ ${\ displaystyle \ partial B ^ {n}}$ a discului. Ca spațiu topologic , ${\overline {\mathbb {H} ^{n}}}$ ${\ displaystyle {\ overline {\ mathbb {H} ^ {n}}}}$ ${\ displaystyle {\ overline {\ mathbb {H} ^ {n}}}}$ este homeomorf pentru discul închis

D^{n}=\{x\in \mathbb {R} ^{n}\ |\ |x|\leq 1\}=B^{n}\cup S^{n-1}.

{\ displaystyle D ^ {n} = \ {x \ in \ mathbb {R} ^ {n} \ | \ | x | \ leq 1 \} = B ^ {n} \ cup S ^ {n-1}. }

{\ displaystyle D ^ {n} = \ {x \ in \ mathbb {R} ^ {n} \ | \ | x | \ leq 1 \} = B ^ {n} \ cup S ^ {n-1}. }

Prin urmare, este un spațiu compact . Procesul de compactificare prin adăugarea „punctelor la infinit” este similar cu trecerea de la Euclidean la spațiul proiectiv .

Tipuri de izometrii

O izometrie a spațiului hiperbolic

f:\mathbb {H} ^{n}\to \mathbb {H} ^{n}

{\ displaystyle f: \ mathbb {H} ^ {n} \ to \ mathbb {H} ^ {n}}

{\ displaystyle f: \ mathbb {H} ^ {n} \ to \ mathbb {H} ^ {n}}

se întinde până la margine. Adică, există un singur homeomorfism

{\bar {f}}:{\overline {\mathbb {H} ^{n}}}\to {\overline {\mathbb {H} ^{n}}}

{\ displaystyle {\ bar {f}}: {\ overline {\ mathbb {H} ^ {n}}} \ to {\ overline {\ mathbb {H} ^ {n}}}}

{\ displaystyle {\ bar {f}}: {\ overline {\ mathbb {H} ^ {n}}} \ to {\ overline {\ mathbb {H} ^ {n}}}}

care coincide cu $f$ ${\ displaystyle f}$ $f$ în interiorul discului, adică pe $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ .

Teorema punctului fix al lui Brouwer afirmă că fiecare homeomorfism al discului închis $D^{n}$ ${\ displaystyle D ^ {n}}$ $D ^ {n}$ în sine are un punct fix . Această teoremă, care nu este valabilă pe mingea deschisă $B^{n}$ ${\ displaystyle B ^ {n}}$ ${\ displaystyle B ^ {n}}$ , garantează astfel existența unui punct fix pentru funcția extinsă ${\bar {f}}$ ${\ displaystyle {\ bar {f}}}$ ${\ displaystyle {\ bar {f}}}$ (dar nu pentru $f$ ${\ displaystyle f}$ $f$ ).

O izometrie $f$ ${\ displaystyle f}$ $f$ care păstrează orientarea spațiului hiperbolic se numește:

eliptic dacă are un punct fix la $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ,
parabolică dacă nu are puncte fixe în $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ și are una pe margine $\partial \mathbb {H} ^{n}$ ${\ displaystyle \ partial \ mathbb {H} ^ {n}}$ ${\ displaystyle \ partial \ mathbb {H} ^ {n}}$ ,
hiperbolic dacă nu are puncte fixe în $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ și are două pe margine $\partial \mathbb {H} ^{n}$ ${\ displaystyle \ partial \ mathbb {H} ^ {n}}$ ${\ displaystyle \ partial \ mathbb {H} ^ {n}}$ .

Nu există alte posibilități în afară de cele enumerate.

Soiuri hiperbolice complete

Fiecare varietate hiperbolică completă poate fi obținută ca un coeficient al spațiului hiperbolic pentru un grup de izometrii care acționează într-un mod liber și corect discontinuu. În special, o astfel de izometrie nu trebuie să aibă puncte fixe în $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ .

Dacă varietatea hiperbolică este orientabilă , grupul este format din izometrii care păstrează orientarea. Astfel de izometrii sunt, prin urmare, hiperbolice sau parabolice (elipticele sunt excluse deoarece au puncte fixe în $\mathbb {H} ^{n}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ${\ displaystyle \ mathbb {H} ^ {n}}$ ). Dacă varietatea este compactă , toate izometriile sunt hiperbolice.

Planul hiperbolic

Geometrie hiperbolică

Planul hiperbolic reprezentat de discul Poincaré .

Același subiect în detaliu: geometria hiperbolică .

Planul hiperbolic este spațiul hiperbolic $\mathbb {H} ^{2}$ ${\ displaystyle \ mathbb {H} ^ {2}}$ ${\ displaystyle \ mathbb {H} ^ {2}}$ bidimensională. Este cel mai studiat spațiu hiperbolic și primul care a fost introdus istoric, ca exemplu de geometrie hiperbolică și, prin urmare , neeuclidiană . La nivel hiperbolic, primele patru axiome ale lui Euclid sunt valabile:

Între oricare două puncte este posibilă trasarea unei singure linii drepte .
Puteți extinde o linie dincolo de două puncte pe termen nelimitat.
Având în vedere un punct și o lungime, este posibil să se descrie un cerc .
Toate unghiurile drepte sunt aceleași.

dar al cincilea nu este adevărat:

Având în vedere orice linie dreaptă

r

{\ displaystyle r}

r

și un punct

P.

{\ displaystyle P}

P.

nu aparținând acestuia, puteți urmări

P.

{\ displaystyle P}

P.

o singură linie paralelă cu linia

r

{\ displaystyle r}

r

Data.

Această ultimă axiomă trebuie de fapt înlocuită cu următoarea:

Având în vedere orice linie dreaptă

r

{\ displaystyle r}

r

și un punct

P.

{\ displaystyle P}

P.

nu aparținând acestuia, puteți urmări

P.

{\ displaystyle P}

P.

linii infinite paralele cu linia

r

{\ displaystyle r}

r

Data.

Spațiul hiperbolic tridimensional

Spațiul hiperbolic tridimensional $\mathbb {H} ^{3}$ ${\ displaystyle \ mathbb {H} ^ {3}}$ ${\ mathbb H} ^ {3}$ a făcut obiectul unor studii intense efectuate de matematicieni, mai ales de la sfârșitul anilor șaptezeci , adică la mai bine de un secol după introducerea planului hiperbolic. Interesul brusc pentru spațiul hiperbolic se datorează studiilor lui William Thurston , care au arătat în mod neașteptat importanța enormă a geometriei hiperbolice în studiul varietăților diferențiate ale dimensiunii 3.

Bibliografie

( EN ) Riccardo Benedetti, Carlo Petronio, Lectures on hyperbolic geometry , Springer, 1992.
(EN) John Milnor , Geometrie hiperbolică: primii 150 de ani, în Buletinul Societății Americane de Matematică, vol. 6, nr. 1, 1982.

Elemente conexe

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică