Solid arhimedean
În geometrie , un solid arhimedean sau semiregular este un poliedru convex ale cărui fețe sunt formate din două sau mai multe tipuri de poligoane regulate și ale căror vârfuri sunt omogene. De asemenea, este necesar ca poliedrul să nu fie o prismă sau un antiprism . Solidele arhimediene sunt 13 și diferă de solidele platonice (sau regulate ), care au și fețe omogene, și de solidele Johnson , ale căror vârfuri nu sunt omogene.
Definiție
Un solid arhimedean sau semiregular este un poliedru convex care îndeplinește următoarele proprietăți:
- Fețele sale sunt poligoane regulate .
- Vârfurile sunt omogene : adică pentru fiecare pereche dintre acestea există o simetrie a solidului care îl mută pe primul în al doilea.
- Solidul nu este un solid platonic , nici o prismă , nici un anti-prismă .
Un solid arhimedean are cel puțin două tipuri distincte de fețe: solidele care satisfac primele două ipoteze și au un singur tip de față sunt solidele platonice (sau regulate ). Solidele arhimediene sunt, așadar, într-un anumit sens, cele mai „regulate” solide după cele platonice (de unde și termenul „semiregular”).
Prismele și antiprismele nu sunt considerate în mod tradițional arhimedice, deși satisfac primele două ipoteze. Prismele și antiprismele diferă calitativ de solidele arhimediene pentru doi factori:
- Prismele și antiprismele formează două familii infinite de solide, în timp ce solidele arhimedee au un număr finit (13)
- Prismele și antiprismele admit „puține” simetrii ( grupul lor de simetrie este grupul diedru , un grup „mai ușor” al grupelor de simetrie ale solilor arhimedici).
Originea numelui
Solidele arhimedee își derivă numele de la Arhimede , care le-a tratat într-o lucrare acum pierdută. În timpul Renașterii, diverși artiști matematici au redescoperit toate aceste poliedre bogate în simetrii în îmbunătățirea formelor pure . Această cercetare a fost finalizată în jurul anului 1619 de Kepler , care a redefinit prismele , antiprismele și două dintre poliedrele neconvexe obișnuite numite acum solide Kepler-Poinsot .
Proprietate
Vârfuri
Deoarece vârfurile sunt omogene, toate sunt la fel. Mai precis, cuspizii din jurul vârfurilor sunt identici (pot fi obținuți unul de la altul prin rotație ).
Margini
Marginile unui poliedru arhimedian au toate aceeași lungime: acest lucru se datorează faptului că fețele sunt toate poligoane regulate. Lungimea a unei muchii este deci un parametru care determină dimensiunea globală a poliedrului: variații ale transformă poliedrul prin comparație . În consecință, volumul și suprafața unui poliedru arhimedian sunt calculate în funcție de .
Clasificare
Există 13 solide arhimedeice, dintre care două sunt chirale , adică nu sunt echivalente cu imaginea lor reflectată: din acest motiv, în unele contexte aceste poliedre sunt numărate de două ori și vorbim de 15 solide arhimedeice.
În tabelul următor, incidența vârfurilor înseamnă secvența numerelor de laturi care caracterizează poligoanele regulate care afectează fiecare vârf. De exemplu, incidența (4,6,8) înseamnă că un pătrat, un hexagon și un octagon afectează fiecare vârf; o astfel de secvență este specificată procedând în sensul acelor de ceasornic în jurul vârfului.
Grupul de simetrie al solidului O h , I h și T d este grupul de simetrie al octaedrului , icosaedrului și respectiv tetraedrului . Grupurile O și I sunt subgrupurile lui O h și respectiv I h formate din simetriile care păstrează orientarea .
| Nume | Imagine | Fețe | Margini | Vârfuri | Incidența managementului de vârf | Grup de simetrie | |
|---|---|---|---|---|---|---|---|
| cuboctaedru | 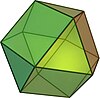 ( Animație ) | 14 | 8 triunghiuri 6 pătrate | 24 | 12 | 3,4,3,4 | O h |
| icosidodecaedru | 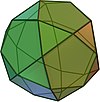 ( Animație ) | 32 | 20 de triunghiuri 12 pentagone | 60 | 30 | 3,5,3,5 | Eu h |
| tetraedru trunchiat | 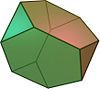 ( Animație ) | 8 | 4 triunghiuri 4 hexagone | 18 | 12 | 3,6,6 | T d |
| cub trunchiat (sau hexaedru trunchiat) |  ( Animație ) | 14 | 8 triunghiuri 6 octogonuri | 36 | 24 | 3.8.8 | O h |
| octaedru trunchiat |  ( Animație ) | 14 | 6 pătrate 8 hexagone | 36 | 24 | 4,6,6 | O h |
| dodecaedru trunchiat |  ( Animație ) | 32 | 20 de triunghiuri 12 decagonuri | 90 | 60 | 3.10.10 | Eu h |
| icosaedru trunchiat (sau mingea de fotbal) |  ( Animație ) | 32 | 12 pentagone 20 de hexagone | 90 | 60 | 5.6.6 | Eu h |
| rombicuboctaedru (sau mic rombicuboctaedru) |  ( Animație ) | 26 | 8 triunghiuri 18 pătrate | 48 | 24 | 3,4,4,4 | O h |
| cuboctaedru trunchiat (sau rombicuboctaedru mare) | 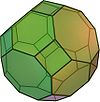 ( Animație ) | 26 | 12 pătrate 8 hexagone 6 octogonuri | 72 | 48 | 4,6,8 | O h |
| rombicosidodecaedru (sau mic rombicosidodecaedru) |  ( Animație ) | 62 | 20 de triunghiuri 30 de pătrate 12 pentagone | 120 | 60 | 3,4,5,4 | Eu h |
| icosidodecaedru trunchiat (sau rombicosidodecaedru mare) |  (Animație ) | 62 | 30 de pătrate 20 de hexagone 12 decagonuri | 180 | 120 | 4,6,10 | Eu h |
| cub snub (sau cuboctaedru snub) 2 forme chirale |  ( Animație )  ( Animație ) | 38 | 32 de triunghiuri 6 pătrate | 60 | 24 | 3,3,3,3,4 | SAU |
| snod dodecaedru (sau snob icosidodecaedru) 2 forme chirale |  ( Animație )  ( Animație ) | nouăzeci și doi | 80 de triunghiuri 12 pentagone | 150 | 60 | 3,3,3,3,5 | THE |
Poliedre aproape regulate
Primele două poliedre, cuboctaedrul și icosidodecaedrul, au (pe lângă vârfuri) și margini omogene: pentru fiecare pereche de margini există o simetrie a poliedrului care mută prima în a doua. Poliedrele cu această proprietate se numesc cvasiregulare (nu trebuie confundate cu semiregulare , sinonime cu arhimedeo ).
Poliedre chirale
Ultimele două, cubul snub și dodecaedrul snub sunt poliedre chirale , poliedre care nu sunt echivalente cu imaginea lor reflectată . Prin urmare, acestea au două forme, levomorfe și dextromorfe , care (precum mâinile) se transformă una în cealaltă atunci când sunt supuse unei reflexii față de un plan.
Cum să obțineți un solid arhimedean
Solidele arhimediene pot fi obținute prin trunchierea unui solid platonic sau a unui alt solid arhimedian pentru a obține un poliedru care respectă proprietățile solidelor semi-regulate:
De la tetraedru la octaedru
| Tetraedru | Tetraedru trunchiat | Octaedru |
|---|---|---|
 |  |  |
De la cub la octaedru
| cub | Cub trunchiat | Cuboctaedru | Otaedru trunchiat | Octaedru |
|---|---|---|---|---|
 |  |  |  | |
De la cuboctaedru la rombicuboctaedru
| Cuboctaedru | Cuboctaedru trunchiat | Rombicuboctaedru |
|---|---|---|
|  |  |
De la dodecaedru la icosaedru
| Dodecaedru | Dodecaedru trunchiat | Icosidodecaedru | Icosaedru trunchiat | Icosaedru |
|---|---|---|---|---|
 |  |  |  |  |
De la icosidodecaedru la rombicosidodecaedru
| Icosidodecaedru | Icosidodecaedru trunchiat | Rombicosidodecaedru |
|---|---|---|
|  |  |
Poliedre duale
Poliedrele duale ale solidelor arhimediene se numesc solide catalane . Relația de dualitate schimbă rolurile vârfurilor și fețelor: deoarece poliedrele arhimediene au vârfuri omogene (dar nu fețe), cele din catalană au fețe omogene (dar nu vârfuri).
Bibliografie
- Henry Martin Cundy și AP Rollett, Modelele matematice , Milano, Feltrinelli, 1974.
- Maria Dedò, Forme, simetrie și topologie , Bologna, Decibel și Zanichelli, 1999, ISBN 88-08-09615-7 .
- L. Berzolari, G. Vivanti, D. Gigli (editat de), Enciclopedia matematicii elementare , Milano, Ulrico Hoepli, 1979, ISBN 88-203-0265-9 .
Alte proiecte
-
Wikimedia Commons conține imagini sau alte fișiere pe solid Archimedean
linkuri externe
- Modele de hârtie de solide Archimedean , pe software3d.com .
- Poliedrele uniforme , pe mathconsult.ch .
- Virtual Reality Polyhedra Enciclopedia poliedrelor
- Penultimul Origami Modular , pe cs.utk.edu .
- Solid Archimedean în MathWorld
| Controlul autorității | GND ( DE ) 4122830-3 |
|---|
