Câmp electric

În fizică , câmpul electric este un câmp al forțelor generate în spațiu de prezența uneia sau mai multor sarcini electrice sau a unui câmp magnetic care variază în timp. Împreună cu câmpul magnetic constituie câmpul electromagnetic , responsabil pentru interacțiunea electromagnetică .

Introdus de Michael Faraday , câmpul electric se propagă cu viteza luminii și exercită o forță asupra oricărui obiect încărcat electric. În sistemul internațional de unități este măsurat în newtoni per coulomb (N / C) sau în volți pe metru (V / m). Dacă este generat doar de distribuția staționară a sarcinii spațiale, câmpul electric se numește electrostatic și este conservator .

Dacă este prezent într-un material conductor, câmpul electric generează un curent electric .

Dovezi experimentale

Atracția sau respingerea între corpurile încărcate electric are loc experimental, corespunzând a două stări de electrificare a materiei. Sarcina este definită ca pozitivă atunci când există o lipsă de electroni în obiect, negativă în prezența unui exces. Ambele corpuri electrificate pozitiv sau negativ se resping reciproc, în timp ce corpurile electrificate în mod opus se atrag reciproc.

Pentru a măsura electrificarea unui corp, se folosește un instrument numit electroscop cu frunze, format dintr-o fiolă de sticlă în care se introduce o tijă metalică care, în interiorul fiolei, are două cleme metalice foarte subțiri, numite frunze , în timp ce la exterior poate fi pus în contact cu un corp încărcat. Prin plasarea unui corp încărcat în contact cu tija, clapele se îndepărtează una de cealaltă proporțional cu electrificarea corpului care a fost adus în contact.

Pornind de la aceste dovezi experimentale, în a doua jumătate a secolului al XVIII-lea, Charles Augustin de Coulomb a formulat legea lui Coulomb , care cuantifică forța electrică atractivă sau respingătoare pe care o schimbă la distanță două corpuri punctiforme încărcate electric. Pornind de la această lege, se poate afirma că un corp încărcat electric produce un câmp în spațiul înconjurător astfel încât, dacă este introdusă o sarcină electrică, este afectată de efectul unei forțe , numită forță Coulomb , direct proporțională cu produsul cele două încărcături și invers proporționale cu pătratul distanței lor.

Câmp electrostatic în vid

În vid, câmpul electric $\mathbf {E}$ ${\ displaystyle \ mathbf {E}}$ $\ mathbf E$ la un punct din spațiu este definit ca forța pe unitate de sarcină electrică pozitivă la care este supusă o sarcină punctuală $q$ ${\ displaystyle q}$ $q$ , denumită acuzație de „proces”, dacă este plasată în punctul: ^[1] ^[2]

\mathbf {E} =\lim _{q\to 0}{\frac {\mathbf {F} }{q}}

{\ displaystyle \ mathbf {E} = \ lim _ {q \ to 0} {\ frac {\ mathbf {F}} {q}}}

{\ mathbf E} = \ lim _ {{q \ to 0}} {\ frac {{\ mathbf F}} {q}}

Poziția unei încărcături punctuale în spațiul euclidian. Câmpul generat în poziție

\mathbf {r}

{\ displaystyle \ mathbf {r}}

\ mathbf r

este proporțională cu valoarea încărcăturii plasate în punct

\mathbf {r} _{q}

{\ displaystyle \ mathbf {r} _ {q}}

{\ mathbf r} _ {q}

și invers proporțional cu pătratul distanței

\mathbf {r} -\mathbf {r} _{q}

{\ displaystyle \ mathbf {r} - \ mathbf {r} _ {q}}

{\ mathbf r} - {\ mathbf r} _ {q}

a taxei.

Vectorul câmpului electric $\mathbf {E}$ ${\ displaystyle \ mathbf {E}}$ $\ mathbf E$ într-un punct, prin urmare, este definit ca raportul dintre forța electrică care acționează asupra sarcinii de testare și valoarea sarcinii în sine, cu condiția ca sarcina de testare să fie suficient de mică pentru a provoca o perturbare neglijabilă a distribuției eventuale a sarcinii care generează câmpul. Prin urmare, câmpul este independent de valoarea sarcinii de test utilizate, relația dintre forță și sarcina însăși fiind independentă, iar acest lucru arată că câmpul electric este o proprietate caracteristică a spațiului. Din definiție rezultă că unitatea de măsură a câmpului electric este $\mathrm {N} /\mathrm {C}$ ${\ displaystyle \ mathrm {N} / \ mathrm {C}}$ ${\ displaystyle \ mathrm {N} / \ mathrm {C}}$ , care este echivalent cu $\mathrm {V} /\mathrm {m}$ ${\ displaystyle \ mathrm {V} / \ mathrm {m}}$ ${\ displaystyle \ mathrm {V} / \ mathrm {m}}$ .

Din legea lui Coulomb rezultă că o acuzație $Î$ ${\ displaystyle Q}$ $Î$ asezat in $\mathbf {r} '$ ${\ displaystyle \ mathbf {r} '}$ ${\ mathbf r} '$ generează un câmp electric care în orice moment $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ este definit de următoarea expresie:

\mathbf {E} (\mathbf {r} )={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {\mathbf {r} -\mathbf {r} '}{\left\|\mathbf {r} -\mathbf {r} '\right\|^{3}}}

{\ displaystyle \ mathbf {E} (\ mathbf {r}) = {\ frac {Q} {4 \ pi \ varepsilon _ {0}}} {\ frac {\ mathbf {r} - \ mathbf {r} ' } {\ left \ | \ mathbf {r} - \ mathbf {r} '\ right \ | ^ {3}}}}

{\ mathbf E} ({\ mathbf r}) = {\ frac {Q} {4 \ pi \ varepsilon _ {0}}} {\ frac {{\ mathbf r} - {\ mathbf r} '} {\ left \ | {\ mathbf r} - {\ mathbf r} '\ right \ | ^ {3}}}

unde este $\varepsilon _{0}$ ${\ displaystyle \ varepsilon _ {0}}$ $\ varepsilon _ {{0}}$ este constanta dielectrică a vidului .
Pentru un număr n de taxe punctuale $q_{i}$ ${\ displaystyle q_ {i}}$ $q_ {i}$ distribuie câmpul electrostatic în spațiu în poziție $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ este dat de: ^[3]

\mathbf {E} _{0}(\mathbf {r} )=\displaystyle \sum _{i=1}^{n}\mathbf {E} _{0i}(r)={\frac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{n}q_{i}{\frac {\mathbf {r} -\mathbf {r} _{i}'}{\left\|\mathbf {r} -\mathbf {r} _{i}'\right\|^{3}}}

{\ displaystyle \ mathbf {E} _ {0} (\ mathbf {r}) = \ displaystyle \ sum _ {i = 1} ^ {n} \ mathbf {E} _ {0i} (r) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ sum _ {i = 1} ^ {n} q_ {i} {\ frac {\ mathbf {r} - \ mathbf {r} _ {i} '} {\ left \ | \ mathbf {r} - \ mathbf {r} _ {i}' \ right \ | ^ {3}}}}

{\ mathbf E} _ {0} ({\ mathbf r}) = \ displaystyle \ sum _ {{i = 1}} ^ {n} {\ mathbf E} _ {{0i}} (r) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ sum _ {{i = 1}} ^ {n} q_ {i} {\ frac {{\ mathbf r} - {\ mathbf r} _ {i} '} {\ left \ | {\ mathbf r} - {\ mathbf r} _ {i}' \ right \ | ^ {3}}}

În general, pentru o distribuție continuă a sarcinii avem: ^[4]

\mathbf {E} _{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\iiint _{\Omega }\rho (\mathbf {r} '){\frac {\mathbf {r} -\mathbf {r} '}{\left\|\mathbf {r} -\mathbf {r} '\right\|^{3}}}\mathop {\mathrm {d} x'} \mathop {\mathrm {d} y'} \mathop {\mathrm {d} z'}

{\ displaystyle \ mathbf {E} _ {0} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ iiint _ {\ Omega} \ rho (\ mathbf {r} ') {\ frac {\ mathbf {r} - \ mathbf {r}'} {\ left \ | \ mathbf {r} - \ mathbf {r} '\ right \ | ^ {3}}} \ mathop {\ mathrm {d} x '} \ mathop {\ mathrm {d} y'} \ mathop {\ mathrm {d} z '}}

{\ displaystyle \ mathbf {E} _ {0} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ iiint _ {\ Omega} \ rho (\ mathbf {r} ') {\ frac {\ mathbf {r} - \ mathbf {r}'} {\ left \ | \ mathbf {r} - \ mathbf {r} '\ right \ | ^ {3}}} \ mathop {\ mathrm {d} x '} \ mathop {\ mathrm {d} y'} \ mathop {\ mathrm {d} z '}}

unde este $\rho (\mathbf {r} )$ ${\ displaystyle \ rho (\ mathbf {r})}$ $\ rho ({\ mathbf r})$ reprezintă densitatea de încărcare în spațiu:

\rho (\mathbf {r} )=\lim _{\Delta V\to 0}{\frac {\Delta q}{\Delta V}}={\frac {\mathop {\mathrm {d} q} }{\mathop {\mathrm {d} V} }}

{\ displaystyle \ rho (\ mathbf {r}) = \ lim _ {\ Delta V \ to 0} {\ frac {\ Delta q} {\ Delta V}} = {\ frac {\ mathop {\ mathrm {d } q}} {\ mathop {\ mathrm {d} V}}}}

{\ displaystyle \ rho (\ mathbf {r}) = \ lim _ {\ Delta V \ to 0} {\ frac {\ Delta q} {\ Delta V}} = {\ frac {\ mathop {\ mathrm {d } q}} {\ mathop {\ mathrm {d} V}}}}

Și $\Omega$ ${\ displaystyle \ Omega}$ $\Omega$ reprezintă regiunea spațiului ocupat de distribuția sarcinii. Câmpul electric poate fi exprimat ca un gradient al unui potențial scalar , potențialul electric : ^[5]

\mathbf {E} _{0}=-\operatorname {grad} V_{0}=-\nabla V_{0}

{\ displaystyle \ mathbf {E} _ {0} = - \ operatorname {grad} V_ {0} = - \ nabla V_ {0}}

{\ mathbf {E}} _ {0} = - \ operatorname {grad} V_ {0} = - \ nabla V_ {0}

Deoarece potențialul electric este un câmp scalar , câmpul electric este conservator.

Liniile de curgere și teorema lui Gauss

Același subiect în detaliu: Teorema fluxului .

Linii de flux de ieșire pentru câmpul electric produse de o sarcină pozitivă în spațiu

Linii de flux de intrare pentru câmpul electric produse de o sarcină negativă în spațiu

Linii de flux produse de două sarcini egale și opuse ale semnului în spațiu - dipol electric

Linii de flux produse de două sarcini egale și de același semn în spațiu

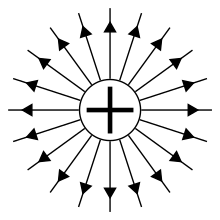
Câmpul electric este un câmp vector reprezentat prin linii de câmp: o sarcină punct pozitivă produce liniile de câmp radial care ies din acesta și este definită ca sursa liniilor de forță, în timp ce pentru o sarcină punct negativă liniile câmpului sunt radiale și de intrare spre sarcină, care este astfel definită ca un puț de linii de forță. Liniile de nivel de potențial electric constant sunt numite suprafețe echipotențiale și sunt perpendiculare pe liniile de flux ale câmpului electric.

Faptul că o suprafață închisă care închide sursa câmpului este traversată de toate liniile de forță generate de sursă este formalizată prin teorema fluxului, numită și teorema lui Gauss, care definește o proprietate matematică generală pentru câmpul electric electric. În vid, teorema afirmă că fluxul câmpului electric printr-o suprafață închisă conținând o distribuție a sarcinii caracterizată prin densitatea volumică a sarcinii $\rho$ ${\ displaystyle \ rho}$ $\ rho$ este egală cu sarcina totală conținută în volumul închis de suprafață împărțit la constanta dielectrică a vidului : ^[6]

\Phi _{\Sigma }(\mathbf {E} )={\frac {1}{\varepsilon _{0}}}\int _{V}\rho (x,y,z)\mathop {\mathrm {d} V} ={\frac {Q_{\text{int}}}{\varepsilon _{0}}}

{\ displaystyle \ Phi _ {\ Sigma} (\ mathbf {E}) = {\ frac {1} {\ varepsilon _ {0}}} \ int _ {V} \ rho (x, y, z) \ mathop {\ mathrm {d} V} = {\ frac {Q _ {\ text {int}}} {\ varepsilon _ {0}}}}

{\ displaystyle \ Phi _ {\ Sigma} (\ mathbf {E}) = {\ frac {1} {\ varepsilon _ {0}}} \ int _ {V} \ rho (x, y, z) \ mathop {\ mathrm {d} V} = {\ frac {Q _ {\ text {int}}} {\ varepsilon _ {0}}}}

Aplicând teorema divergenței la prima relație și echivalând integranzii obținem: ^[7]

\mathbf {\nabla } \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}

{\ displaystyle \ mathbf {\ nabla} \ cdot \ mathbf {E} = {\ frac {\ rho} {\ varepsilon _ {0}}}}

{\ mathbf \ nabla} \ cdot {\ mathbf E} = {\ frac {\ rho} {\ varepsilon _ {0}}}

Această ecuație este prima dintre ecuațiile lui Maxwell și constituie forma locală a teoremei lui Gauss pentru câmpul electric.

Circuit de câmp electrostatic

Câmpul electrostatic este generat de o distribuție a sarcinii independentă de timp. O condiție necesară și suficientă pentru ca un câmp vector să fie conservator într-un set simplu conectat , de exemplu, un set înstelat sau convex , este că circuitul câmpului, adică integralul câmpului de-a lungul unei linii închise, este zero: ^[8]

\oint _{\gamma }\mathbf {E} _{0}\cdot \mathop {\mathrm {d} \mathbf {l} } =0

{\ displaystyle \ oint _ {\ gamma} \ mathbf {E} _ {0} \ cdot \ mathop {\ mathrm {d} \ mathbf {l}} = 0}

{\ displaystyle \ oint _ {\ gamma} \ mathbf {E} _ {0} \ cdot \ mathop {\ mathrm {d} \ mathbf {l}} = 0}

Acest lucru se întâmplă numai în condiții staționare.

În mod echivalent, câmpul electrostatic este conservator, deoarece există o funcție scalară, potențialul electric , astfel încât integralul să treacă de la un punct A la un punct B nu depinde de calea parcursă, ci doar de valoarea funcției la extreme : ^[9]

\int _{A}^{B}\mathbf {E} _{0}\cdot \mathop {\mathrm {d} \mathbf {l} } =V_{0}(A)-V_{0}(B)

{\ displaystyle \ int _ {A} ^ {B} \ mathbf {E} _ {0} \ cdot \ mathop {\ mathrm {d} \ mathbf {l}} = V_ {0} (A) -V_ {0 } (B)}

{\ displaystyle \ int _ {A} ^ {B} \ mathbf {E} _ {0} \ cdot \ mathop {\ mathrm {d} \ mathbf {l}} = V_ {0} (A) -V_ {0 } (B)}

Ecuațiile lui Maxwell pentru câmpul electrostatic în vid

Același subiect în detaliu: ecuațiile lui Maxwell .

Din teorema divergenței și teorema fluxului obținem prima ecuație Maxwell în vid: ^[7]

\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}

{\ displaystyle \ nabla \ cdot \ mathbf {E} = {\ frac {\ rho} {\ varepsilon _ {0}}}}

\ nabla \ cdot {\ mathbf E} = {\ frac {\ rho} {\ varepsilon _ {0}}}

Pentru conservativitatea câmpului electrostatic este posibil să se afirme a treia ecuație a lui Maxwell în vid în formele: ^[10]

\mathbf {E} _{0}=-\nabla V_{0}\qquad \nabla \times \mathbf {E} =0

{\ displaystyle \ mathbf {E} _ {0} = - \ nabla V_ {0} \ qquad \ nabla \ times \ mathbf {E} = 0}

{\ mathbf E} _ {0} = - \ nabla V_ {0} \ qquad \ nabla \ times {\ mathbf E} = 0

Combinând prima cu a doua obținem ecuația Poisson : ^[11]

\nabla ^{2}V_{0}={\frac {\partial ^{2}V_{0}}{\partial x^{2}}}+{\frac {\partial ^{2}V_{0}}{\partial y^{2}}}+{\frac {\partial ^{2}V_{0}}{\partial z^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}

{\ displaystyle \ nabla ^ {2} V_ {0} = {\ frac {\ partial ^ {2} V_ {0}} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} V_ {0}} {\ partial y ^ {2}}} + {\ frac {\ partial ^ {2} V_ {0}} {\ partial z ^ {2}}} = - {\ frac {\ rho} {\ varepsilon _ {0}}}}

\ nabla ^ {{2}} V_ {0} = {\ frac {\ partial ^ {2} V_ {0}} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} V_ {0}} {\ partial y ^ {2}}} + {\ frac {\ partial ^ {2} V_ {0}} {\ partial z ^ {2}}} = - {\ frac {\ rho} { \ varepsilon _ {0}}}

unde cu $\nabla ^{2}$ ${\ displaystyle \ nabla ^ {2}}$ $\ nabla ^ {2}$ indicăm operatorul diferențial laplacian . Soluția ecuației Poisson este unică dacă sunt date condițiile la limită. În special, un potențial care satisface ecuația Poisson și care este zero la o distanță infinită de sursele câmpului coincide în mod necesar cu potențialul electric , ^[12] dat de expresia:

V_{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{v}{\frac {\rho (x',y',z')}{|\mathbf {r} -\mathbf {r} '|}}\mathop {\mathrm {d} x'} \mathop {\mathrm {d} y'} \mathop {\mathrm {d} z'}

{\ displaystyle V_ {0} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ int _ {v} {\ frac {\ rho (x ', y ', z')} {| \ mathbf {r} - \ mathbf {r} '|}} \ mathop {\ mathrm {d} x'} \ mathop {\ mathrm {d} y '} \ mathop {\ mathrm {d} z '}}

{\ displaystyle V_ {0} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ int _ {v} {\ frac {\ rho (x ', y ', z')} {| \ mathbf {r} - \ mathbf {r} '|}} \ mathop {\ mathrm {d} x'} \ mathop {\ mathrm {d} y '} \ mathop {\ mathrm {d} z '}}

În absența taxelor sursă în câmp, ecuația devine omogenă și ia numele ecuației lui Laplace :

\nabla ^{2}V=0

{\ displaystyle \ nabla ^ {2} V = 0}

\ nabla ^ {{2}} V = 0

.

din care rezultă că în absența sarcinilor potențialul este o funcție armonică .

Condiții de frontieră

Rezolvarea ecuației Poisson în regiuni limitate ale spațiului înseamnă rezolvarea problemei generale a electrostaticelor pentru condiții limită adecvate, cum ar fi absența sau prezența conductoarelor și sarcinile electrice localizate. În special, se disting trei tipuri:

Condițiile la limita Dirichlet

Același subiect în detaliu: Condițiile la limita Dirichlet .

În acest caz nu există sarcini localizate, iar câmpul electrostatic este generat de un sistem de conductori de geometrie și potențial cunoscut. În acest caz, se menține ecuația Laplace, unde condițiile la limită sunt că potențialul este zero la infinit și se menține $V_{0i}$ ${\ displaystyle V_ {0i}}$ $V _ {{0i}}$ pe suprafața conductoarelor. Odată ce potențialele pentru fiecare punct din spațiu au fost obținute prin rezolvarea ecuației Laplace, se obține câmpul electrostatic și este posibil să se determine densitatea sarcinii de suprafață $\sigma _{i}$ ${\ displaystyle \ sigma _ {i}}$ $\ sigma _ {i}$ pe dirijori folosind teorema lui Coulomb . ^[12] În cele din urmă, sarcina netă totală pe toți conductorii și coeficienții de capacitate pe aceștia pot fi găsiți prin intermediul sistemului următor ^[13] , care permite derivarea coeficienților.

{\begin{cases}Q_{1}=c_{11}V_{01}+c_{12}V_{02}+\cdots +c_{1n}V_{0n}\\Q_{2}=c_{21}V_{01}+c_{22}V_{02}+\cdots +c_{2n}V_{0n}\\\vdots \\Q_{n}=c_{n1}V_{01}+c_{n2}V_{02}+\cdots +c_{nn}V_{0n}\end{cases}}

{\ displaystyle {\ begin {cases} Q_ {1} = c_ {11} V_ {01} + c_ {12} V_ {02} + \ cdots + c_ {1n} V_ {0n} \\ Q_ {2} = c_ {21} V_ {01} + c_ {22} V_ {02} + \ cdots + c_ {2n} V_ {0n} \\\ vdots \\ Q_ {n} = c_ {n1} V_ {01} + c_ {n2} V_ {02} + \ cdots + c_ {nn} V_ {0n} \ end {cases}}}

{\ displaystyle {\ begin {cases} Q_ {1} = c_ {11} V_ {01} + c_ {12} V_ {02} + \ cdots + c_ {1n} V_ {0n} \\ Q_ {2} = c_ {21} V_ {01} + c_ {22} V_ {02} + \ cdots + c_ {2n} V_ {0n} \\\ vdots \\ Q_ {n} = c_ {n1} V_ {01} + c_ {n2} V_ {02} + \ cdots + c_ {nn} V_ {0n} \ end {cases}}}

Condițiile la limita Neumann

Același subiect în detaliu: condițiile la limita Neumann .

În acest caz câmpul electrostatic este dat de un sistem de conductori de geometrie cunoscută ale căror sarcini pe fiecare sunt cunoscute. Prin urmare, există potențiale arbitrare asupra conductorilor $V_{0}=V_{0i}^{p}$ ${\ displaystyle V_ {0} = V_ {0i} ^ {p}}$ $V _ {{0}} = V _ {{0i}} ^ {p}$ iar problema Dirichlet este rezolvată ca mai sus. Deoarece taxele sunt cunoscute și coeficienții de capacitate sunt independenți de taxe și potențiale, fiind dependenți doar de raportul lor, potențialele reale sunt obținute din sistemul cazului anterior $V_{0}=V_{0i}$ ${\ displaystyle V_ {0} = V_ {0i}}$ $V _ {{0}} = V _ {{0i}}$ . ^[13]

Condiții de graniță mixte

Un exemplu ar putea fi distribuirea taxelor $\rho$ ${\ displaystyle \ rho}$ $\ rho$ nota în spațiu și un sistem de conductori din care sunt cunoscute doar sarcinile de pe fiecare. Problema este rezolvarea ecuației Poisson și, deoarece potențialele nu sunt cunoscute, problema devine un sistem de ecuații precum: ^[13]

V_{i}=V_{i}(\rho )+\sum _{i}^{N}p_{ij}Q_{j}

{\ displaystyle V_ {i} = V_ {i} (\ rho) + \ sum _ {i} ^ {N} p_ {ij} Q_ {j}}

V_ {i} = V_ {i} (\ rho) + \ sum _ {i} ^ {N} p _ {{ij}} Q_ {j}

unde numerele $p_{ij}$ ${\ displaystyle p_ {ij}}$ $p _ {{ij}}$ sunt coeficienții matricei potențiale. Metoda potențialului de testare este apoi utilizată pentru a calcula potențialele. ^[14]

Câmp electric în condiții non-staționare

Electrostatica și magnetostatica reprezintă două cazuri particulare ale unei teorii mai generale, electrodinamica , deoarece tratează cazuri în care câmpurile electrice și magnetice nu variază în timp. În condiții staționare, câmpul electric și câmpul magnetic pot fi de fapt tratate independent unul de celălalt, cu toate acestea, în condiții non-staționare, cele două câmpuri apar ca manifestări ale aceleiași entități fizice: câmpul electromagnetic . ^[15]

Aceleași încărcături care sunt sursa câmpului electric, de fapt, atunci când sunt în mișcare generează un câmp magnetic. Acest fapt este descris de cele două legi fizice care corelează fenomenele electrice și magnetice: legea Ampere-Maxwell și legea lui Faraday simetrică, descrise mai jos.

Legea lui Faraday

Același subiect în detaliu: Legea lui Faraday .

Legea lui Faraday afirmă că forța electromotivă indusă într-un circuit închis de un câmp magnetic este egală cu opusul variației fluxului magnetic al câmpului prin zona îmbrățișată de circuit în unitatea de timp: ^[16]

{\text{f.e.m. }}=-{\mathrm {d} \Phi _{B} \over \mathrm {d} t}

{\ displaystyle {\ text {fem}} = - {\ mathrm {d} \ Phi _ {B} \ over \ mathrm {d} t}}

{\ displaystyle {\ text {f.e.m. }} = - {\ mathrm {d} \ Phi _ {B} \ over \ mathrm {d} t}}

unde este $\Phi _{B}$ ${\ displaystyle \ Phi _ {B}}$ $\ Phi _ {B}$ este fluxul câmpului magnetic $\mathbf {B}$ ${\ displaystyle \ mathbf {B}}$ $\ mathbf B$ . Din definiția forței electromotoare , relația anterioară poate fi scrisă ca:

\oint _{C}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\mathrm {d}  \over \mathrm {d} t}\int _{S}\mathbf {B} \cdot {\mbox{d}}\mathbf {S} =-\int _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot {\mbox{d}}\mathbf {S}

{\ displaystyle \ oint _ {C} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - {\ mathrm {d} \ over \ mathrm {d} t} \ int _ {S} \ mathbf {B} \ cdot {\ mbox {d}} \ mathbf {S} = - \ int _ {S} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ cdot {\ mbox { d}} \ mathbf {S}}

{\ displaystyle \ oint _ {C} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - {\ mathrm {d} \ over \ mathrm {d} t} \ int _ {S} \ mathbf {B} \ cdot {\ mbox {d}} \ mathbf {S} = - \ int _ {S} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ cdot {\ mbox { d}} \ mathbf {S}}

aplicând teorema rotorului la primul element:

\oint _{C}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =\int _{S}(\nabla \times \mathbf {E} )\cdot {\mbox{d}}\mathbf {S}

{\ displaystyle \ oint _ {C} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = \ int _ {S} (\ nabla \ times \ mathbf {E}) \ cdot {\ mbox { d}} \ mathbf {S}}

{\ displaystyle \ oint _ {C} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = \ int _ {S} (\ nabla \ times \ mathbf {E}) \ cdot {\ mbox { d}} \ mathbf {S}}

ajungem la:

\int _{S}(\nabla \times \mathbf {E} )\cdot {\mbox{d}}\mathbf {S} =-\int _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot {\mbox{d}}\mathbf {S}

{\ displaystyle \ int _ {S} (\ nabla \ times \ mathbf {E}) \ cdot {\ mbox {d}} \ mathbf {S} = - \ int _ {S} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ cdot {\ mbox {d}} \ mathbf {S}}

{\ displaystyle \ int _ {S} (\ nabla \ times \ mathbf {E}) \ cdot {\ mbox {d}} \ mathbf {S} = - \ int _ {S} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ cdot {\ mbox {d}} \ mathbf {S}}

Egalizarea integrandilor urmează forma locală a legii lui Faraday, care reprezintă a treia ecuație a lui Maxwell: ^[17] ^[18]

\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}

{\ displaystyle \ nabla \ times \ mathbf {E} = - {\ frac {\ partial \ mathbf {B}} {\ partial t}}}

\ nabla \ times {\ mathbf {E}} = - {\ frac {\ partial {\ mathbf {B}}} {\ partial t}}

Adică, câmpul electric poate fi generat de un câmp magnetic care variază în timp. O consecință fundamentală a legii lui Faraday este că câmpul electric în condiții non-staționare nu mai este conservator, deoarece circulația acestuia nu mai este zero. Mai mult, după ce am definit:

\mathbf {B} =\nabla \times \mathbf {A}

{\ displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A}}

\ mathbf {B} = \ nabla \ times \ mathbf {A}

unde este $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf {A}$ este potențialul vector magnetic, din legea lui Faraday rezultă că:

\nabla \times \left(\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}\right)={\boldsymbol {0}}

{\ displaystyle \ nabla \ times \ left (\ mathbf {E} + {\ frac {\ partial \ mathbf {A}} {\ partial t}} \ right) = {\ boldsymbol {0}}}

{\ displaystyle \ nabla \ times \ left (\ mathbf {E} + {\ frac {\ partial \ mathbf {A}} {\ partial t}} \ right) = {\ boldsymbol {0}}}

Deoarece rotorul este definit până la un gradient, avem:

\mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}

{\ displaystyle \ mathbf {E} = - \ nabla \ phi - {\ frac {\ partial \ mathbf {A}} {\ partial t}}}

{\ mathbf {E}} = - \ nabla \ phi - {\ frac {\ partial {\ mathbf {A}}} {\ partial t}}

Câmpul electric este astfel scris în funcție de potențialele asociate câmpului electromagnetic .

Legea lui Ampere-Maxwell

Același subiect în detaliu: Legea lui Ampère și curentul de deplasare .

Extinderea legii lui Ampère la cazul non-staționar arată cum un câmp electric care variază în timp este sursa unui câmp magnetic. Presupunând că suntem în vid, forma locală a legii lui Ampère constituie a patra ecuație Maxwell în cazul staționar:

\nabla \times \mathbf {B} =\mu _{0}\mathbf {J} \

{\ displaystyle \ nabla \ times \ mathbf {B} = \ mu _ {0} \ mathbf {J} \}

\ nabla \ times {\ mathbf B} = \ mu _ {0} {\ mathbf J} \

Această relație este valabilă doar în cazul staționar, deoarece implică faptul că divergența densității curentului este zero, contrazicând astfel ecuația de continuitate pentru curentul electric : ^[19]

\nabla \cdot \mathbf {J} =-{\frac {\partial \rho }{\partial t}}

{\ displaystyle \ nabla \ cdot \ mathbf {J} = - {\ frac {\ partial \ rho} {\ partial t}}}

\ nabla \ cdot {\ mathbf J} = - {\ frac {\ partial \ rho} {\ partial t}}

Pentru a extinde legea lui Ampère la cazul non-staționar, este necesar să se introducă prima lege a lui Maxwell în ecuația de continuitate:

\nabla \cdot \mathbf {J} +{\frac {\partial \rho }{\partial t}}=\nabla \cdot \left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)

{\ displaystyle \ nabla \ cdot \ mathbf {J} + {\ frac {\ partial \ rho} {\ partial t}} = \ nabla \ cdot \ left (\ mathbf {J} + \ varepsilon _ {0} {\ frac {\ partial \ mathbf {E}} {\ partial t}} \ right)}

\ nabla \ cdot \ mathbf J + \ frac {\ partial \ rho} {\ partial t} = \ nabla \ cdot \ left (\ mathbf J + \ varepsilon_0 \ frac {\ partial \ mathbf E} {\ partial t} \ dreapta)

Termenul

\mathbf {J} _{s}=\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}

{\ displaystyle \ mathbf {J} _ {s} = \ varepsilon _ {0} {\ frac {\ partial \ mathbf {E}} {\ partial t}}}

{\ mathbf {J}} _ {s} = \ varepsilon _ {0} {\ frac {\ partial {\ mathbf {E}}} {\ partial t}}

se numește curent de deplasare și trebuie adăugat la densitatea curentului în cazul non-staționar. ^[20]

Prin inserarea densității de curent generalizate astfel obținute în legea lui Ampère: ^[21] ^[22]

\mathbf {\nabla \times B} =\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)

{\ displaystyle \ mathbf {\ nabla \ times B} = \ mu _ {0} \ left (\ mathbf {J} + \ varepsilon _ {0} {\ frac {\ partial \ mathbf {E}} {\ partial t }} \ dreapta)}

\ mathbf {\ nabla \ times B} = \ mu_0 \ left (\ mathbf J + \ varepsilon_0 \ frac {\ partial \ mathbf E} {\ partial t} \ right)

obținem a patra ecuație Maxwell în vid. ^[23] Această expresie arată cum variația temporală a unui câmp electric este sursa unui câmp magnetic.

Câmp electric în prezența dielectricilor

Același subiect în detaliu: Inducție electrică și polarizare electrică .

Prezența materialului dielectric în spațiul în care există un câmp electric $\mathbf {E}$ ${\ displaystyle \ mathbf {E}}$ $\ mathbf E$ editați câmpul în sine. Acest lucru se datorează faptului că atomii și moleculele care alcătuiesc materialul se comportă ca dipoli microscopici și se polarizează în urma aplicării unui câmp electric extern. Efectul polarizării electrice poate fi descris prin urmărirea polarizării dipolilor microscopici la o cantitate vectorială macroscopică, care descrie comportamentul global al materialului supus prezenței unui câmp electric extern. Vectorul intensității polarizării , numit și vectorul polarizării electrice , este indicat de $\mathbf {P}$ ${\ displaystyle \ mathbf {P}}$ ${\ mathbf P}$ , este dipolul electric pe unitate de volum pe care îl posedă materialul.

Polarizarea dielectricului creează o anumită cantitate de sarcină electrică indusă în interiorul materialului, numită sarcină de polarizare $\rho _{p}$ ${\ displaystyle \ rho _ {p}}$ $\ rho _ {p}$ . Introducând această distribuție a sarcinii în prima dintre ecuațiile lui Maxwell, care exprimă forma locală a teoremei fluxului pentru câmpul electric, avem: ^[24]

\nabla \cdot \mathbf {E} ={\frac {1}{\varepsilon _{0}}}(\rho _{f}+\rho _{p})={\frac {1}{\varepsilon _{0}}}(\rho _{f}-\nabla \cdot \mathbf {P} )

{\ displaystyle \ nabla \ cdot \ mathbf {E} = {\ frac {1} {\ varepsilon _ {0}}} (\ rho _ {f} + \ rho _ {p}) = {\ frac {1} {\ varepsilon _ {0}}} (\ rho _ {f} - \ nabla \ cdot \ mathbf {P})}

\ nabla \ cdot {\ mathbf {E}} = {\ frac {1} {\ varepsilon _ {0}}} (\ rho _ {f} + \ rho _ {p}) = {\ frac {1} { \ varepsilon _ {0}}} (\ rho _ {f} - \ nabla \ cdot {\ mathbf {P}})

unde este $\rho _{f}$ ${\ displaystyle \ rho _ {f}}$ $\ rho _ {f}$ este densitatea sarcinilor libere și în al doilea pas a fost utilizată relația dintre densitatea volumică a sarcinii de polarizare și vectorul de polarizare. Prin urmare, avem:

\nabla \cdot (\varepsilon _{0}\mathbf {E} +\mathbf {P} )=\rho _{f}

{\ displaystyle \ nabla \ cdot (\ varepsilon _ {0} \ mathbf {E} + \ mathbf {P}) = \ rho _ {f}}

\ nabla \ cdot (\ varepsilon _ {0} {\ mathbf {E}} + {\ mathbf {P}}) = \ rho _ {f}

.

Argumentul operatorului diferențial este vectorul de inducție electrică, definit ca: ^[25]

\mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P}

{\ displaystyle \ mathbf {D} = \ varepsilon _ {0} \ mathbf {E} + \ mathbf {P}}

{\ mathbf {D}} = \ varepsilon _ {0} {\ mathbf {E}} + {\ mathbf {P}}

Și prima ecuație a lui Maxwell ia forma:

\nabla \cdot \mathbf {D} =\rho -\rho _{p}=\rho _{f}

{\ displaystyle \ nabla \ cdot \ mathbf {D} = \ rho - \ rho _ {p} = \ rho _ {f}}

\ nabla \ cdot {\ mathbf {D}} = \ rho - \ rho _ {p} = \ rho _ {f}

Majoritatea materialelor izolante pot fi tratate ca un dielectric liniar omogen și izotrop, ceea ce înseamnă că există o relație liniară între dipolul indus în material și câmpul electric extern. Aceasta este o aproximare larg utilizată și, în acest caz, câmpurile $\mathbf {E}$ ${\ displaystyle \ mathbf {E}}$ $\ mathbf {E}$ Și $\mathbf {D}$ ${\ displaystyle \ mathbf {D}}$ $\ mathbf {D}$ sunt echivalente cu mai puțin de un factor de scară: ^[26]

\mathbf {D} =\varepsilon _{r}\varepsilon _{0}\mathbf {E}

{\ displaystyle \ mathbf {D} = \ varepsilon _ {r} \ varepsilon _ {0} \ mathbf {E}}

{\ mathbf {D}} = \ varepsilon _ {r} \ varepsilon _ {0} {\ mathbf {E}}

si in consecinta:

\mathbf {P} =(\varepsilon _{r}-1)\varepsilon _{0}\mathbf {E} =\varepsilon _{0}\chi \mathbf {E} ,

{\ displaystyle \ mathbf {P} = (\ varepsilon _ {r} -1) \ varepsilon _ {0} \ mathbf {E} = \ varepsilon _ {0} \ chi \ mathbf {E},}

{\ mathbf {P}} = (\ varepsilon _ {r} -1) \ varepsilon _ {0} {\ mathbf {E}} = \ varepsilon _ {{0}} \ chi {\ mathbf {E}},

Măreția $\varepsilon _{r}$ ${\ displaystyle \ varepsilon _ {r}}$ $\ varepsilon_r$ este constanta dielectrică relativă și depinde de caracteristicile microscopice ale materialului. Dacă materialul nu este omogen, liniar și izotrop, atunci $\varepsilon$ ${\ displaystyle \ varepsilon}$ $\ varepsilon$ depinde de factori precum poziția în interiorul mediului, temperatura sau frecvența câmpului aplicat.

În domeniul frecvenței, pentru un mediu liniar și independent de timp există relația:

\mathbf {D(\omega )} =\varepsilon (\omega )\mathbf {E} (\omega )

{\ displaystyle \ mathbf {D (\ omega)} = \ varepsilon (\ omega) \ mathbf {E} (\ omega)}

{\ mathbf {D (\ omega)}} = \ varepsilon (\ omega) {\ mathbf {E}} (\ omega)

unde este $\omega$ ${\ displaystyle \ omega}$ $\omega$ este frecvența câmpului.

Ecuațiile lui Maxwell în prezența dielectricelor

Același subiect în detaliu: ecuațiile lui Maxwell .

Prin inserarea vectorului de inducție electrică în ecuațiile lui Maxwell în materiale, luând în considerare cazul în care dielectricul este perfect și izotrop și presupunând că există o relație de liniaritate și pentru câmpul magnetic din materiale, avem: ^[27] ^[28]

{\begin{cases}\nabla \cdot \mathbf {D} =\rho \\\\\nabla \cdot \mathbf {B} =0\\\\\nabla \times \mathbf {E} =-{\dfrac {\partial \mathbf {B} }{\partial t}}\\\\\nabla \times \mathbf {H} =\mathbf {j} +{\dfrac {\partial \mathbf {D} }{\partial t}}\\\end{cases}}

{\ displaystyle {\ begin {cases} \ nabla \ cdot \ mathbf {D} = \ rho \\\\\ nabla \ cdot \ mathbf {B} = 0 \\\\\ nabla \ times \ mathbf {E} = - {\ dfrac {\ partial \ mathbf {B}} {\ partial t}} \\\\\ nabla \ times \ mathbf {H} = \ mathbf {j} + {\ dfrac {\ partial \ mathbf {D} } {\ partial t}} \\\ end {cases}}}

{\ displaystyle {\ begin {cases} \ nabla \ cdot \ mathbf {D} = \ rho \\\\\ nabla \ cdot \ mathbf {B} = 0 \\\\\ nabla \ times \ mathbf {E} = - {\ dfrac {\ partial \ mathbf {B}} {\ partial t}} \\\\\ nabla \ times \ mathbf {H} = \ mathbf {j} + {\ dfrac {\ partial \ mathbf {D} } {\ partial t}} \\\ end {cases}}}

unde este $\mathbf {H}$ ${\ displaystyle \ mathbf {H}}$ $\ mathbf {H}$ este câmpul magnetic din materiale și este analogul vectorului de inducție electrică pentru polarizarea magnetică .

Condiții de conectare între dielectric

Având în vedere dielectricele perfecte și izotrope, este posibil să se definească condițiile de conectare ale câmpului electrostatic atunci când acesta traversează două dielectrice de constantă dielectrică relativă $\varepsilon _{1}$ ${\ displaystyle \ varepsilon _ {1}}$ $\ varepsilon _ {1}$ Și $\varepsilon _{2}$ ${\ displaystyle \ varepsilon _ {2}}$ $\ varepsilon _ {2}$ . Pe suprafața de despărțire luați în considerare o suprafață cilindrică a bazelor $\operatorname {d} \mathbf {S}$ ${\ displaystyle \ operatorname {d} \ mathbf {S}}$ $\ operatorname {d} {\ mathbf S}$ și înălțime $\operatorname {d} l$ ${\ displaystyle \ operatorname {d} l}$ $\ operatorname {d} l$ infinitesimal, de un ordin de mărime mai mare decât baza. Applicando il flusso di Gauss uscente dalle basi si evince che il flusso infinitesimo è nullo poiché non vi sono cariche libere localizzate al suo interno: ^[29]

0=\Phi _{\mathbf {D} }=\mathbf {D} _{1}\cdot \operatorname {d} \mathbf {S} +\mathbf {D} _{2}\cdot \operatorname {d} \mathbf {S} =\operatorname {d} S(D_{1}^{n}-D_{2}^{n})

0=\Phi _{\mathbf {D} }=\mathbf {D} _{1}\cdot \operatorname {d} \mathbf {S} +\mathbf {D} _{2}\cdot \operatorname {d} \mathbf {S} =\operatorname {d} S(D_{1}^{n}-D_{2}^{n})

0=\Phi _{{{\mathbf D}}}={\mathbf D}_{1}\cdot \operatorname {d}{\mathbf S}+{\mathbf D}_{2}\cdot \operatorname {d}{\mathbf S}=\operatorname {d}S(D_{{1}}^{{n}}-D_{{2}}^{{n}})

dove $D_{1}^{n}=D_{2}^{n}$ $D_{1}^{n}=D_{2}^{n}$ $D_{1}^{n}=D_{2}^{n}$ sono le componenti normali del campo di spostamento elettrico. In termini di campo elettrico si ha quindi:

\varepsilon _{1}E_{1}^{n}=\varepsilon _{2}E_{2}^{n}

\varepsilon _{1}E_{1}^{n}=\varepsilon _{2}E_{2}^{n}

\varepsilon _{1}E_{{1}}^{{n}}=\varepsilon _{2}E_{2}^{{n}}

Per la componente tangenziale del campo elettrico vale il teorema di Coulomb , ovvero la direzione del campo elettrico è normale alla superficie del conduttore, e pertanto la componente tangenziale si conserva: ^[30]

E_{1}^{t}=E_{2}^{t}

E_{1}^{t}=E_{2}^{t}

E_{1}^{{t}}=E_{2}^{{t}}

In termini di campo di spostamento elettrico:

{\frac {D_{1}^{t}}{\varepsilon _{1}}}={\frac {D_{2}^{t}}{\varepsilon _{2}}}

{\frac {D_{1}^{t}}{\varepsilon _{1}}}={\frac {D_{2}^{t}}{\varepsilon _{2}}}

{\frac {D_{1}^{{t}}}{\varepsilon _{1}}}={\frac {D_{2}^{{t}}}{\varepsilon _{2}}}

Attraversando la superficie di separazione tra due dielettrici perfetti ed isotropi, quindi, la componente normale del campo elettrico subisce una discontinuità mentre quella tangenziale non si modifica, viceversa per il campo di spostamento elettrico. Unendo le due relazioni si ottiene la legge di rifrazione delle linee di forza del campo elettrico:

{\frac {E_{1}^{t}}{\varepsilon _{1}E_{1}^{n}}}={\frac {E_{2}^{t}}{\varepsilon _{2}E_{2}^{n}}}

{\frac {E_{1}^{t}}{\varepsilon _{1}E_{1}^{n}}}={\frac {E_{2}^{t}}{\varepsilon _{2}E_{2}^{n}}}

{\frac {E_{1}^{{t}}}{\varepsilon _{1}E_{1}^{{n}}}}={\frac {E_{2}^{{t}}}{\varepsilon _{2}E_{2}^{{n}}}}

e dunque:

{\frac {\tan \theta _{1}}{\tan \theta _{2}}}={\frac {\varepsilon _{1}}{\varepsilon _{2}}}

{\frac {\tan \theta _{1}}{\tan \theta _{2}}}={\frac {\varepsilon _{1}}{\varepsilon _{2}}}

{\frac {\tan \theta _{1}}{\tan \theta _{2}}}={\frac {\varepsilon _{1}}{\varepsilon _{2}}}

dove

\tan \theta ={\frac {E^{t}}{E^{n}}}

\tan \theta ={\frac {E^{t}}{E^{n}}}

\tan \theta ={\frac {E^{t}}{E^{n}}}

è l'angolo di rifrazione.

Il campo elettromagnetico

Lo stesso argomento in dettaglio: Campo elettromagnetico .

Il campo elettromagnetico è dato dalla combinazione del campo elettrico $\mathbf {E}$ $\mathbf {E}$ $\mathbf E$ e del campo magnetico $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ , solitamente descritti con vettori in uno spazio a tre dimensioni. Il campo elettromagnetico interagisce nello spazio con cariche elettriche e può manifestarsi anche in assenza di esse, trattandosi di un'entità fisica che può essere definita indipendentemente dalle sorgenti che l'hanno generata. In assenza di sorgenti il campo elettromagnetico è detto onda elettromagnetica , ^[31] essendo un fenomeno ondulatorio che non richiede di alcun supporto materiale per diffondersi nello spazio e che nel vuoto viaggia alla velocità della luce . Secondo il modello standard , il quanto della radiazione elettromagnetica è il fotone , mediatore dell' interazione elettromagnetica .

La variazione temporale di uno dei due campi determina il manifestarsi dell'altro: campo elettrico e campo magnetico sono caratterizzati da una stretta connessione, stabilita dalle quattro equazioni di Maxwell . Le equazioni di Maxwell, insieme alla forza di Lorentz , definiscono formalmente il campo elettromagnetico e ne caratterizzano l'interazione con oggetti carichi. Le prime due equazioni di Maxwell sono omogenee e valgono sia nel vuoto che nei mezzi materiali, e rappresentano in forma differenziale la Legge di Faraday e la legge di Gauss per il campo magnetico. Le altre due equazioni descrivono il modo con cui il materiale in cui avviene la propagazione interagisce, polarizzandosi, con il campo elettrico e magnetico, che nella materia sono denotati con $\mathbf {D}$ $\mathbf {D}$ $\mathbf D$ e $\mathbf {H}$ $\mathbf {H}$ $\mathbf H$ . Esse mostrano in forma locale la Legge di Gauss elettrica e la Legge di Ampère-Maxwell .

La forza di Lorentz è la forza $\mathbf {F}$ $\mathbf {F}$ $\mathbf{F}$ che il campo elettromagnetico genera su una carica $q$ ${\displaystyle q}$ $q$ puntiforme:

\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )

\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )

{\mathbf {F}}=q({\mathbf {E}}+{\mathbf {v}}\times {\mathbf {B}})

dove $\mathbf {v}$ $\mathbf {v}$ $\mathbf{v}$ è la velocità della carica.

Le equazioni di Maxwell sono formulate anche in elettrodinamica quantistica , dove il campo elettromagnetico viene quantizzato . Nell'ambito della meccanica relativistica , i campi sono descritti dalla teoria dell' elettrodinamica classica in forma covariante , cioè invariante sotto trasformazione di Lorentz . Nell'ambito della teoria della Relatività il campo elettromagnetico è rappresentato dal tensore elettromagnetico , un tensore a due indici di cui i vettori campo elettrico e magnetico sono particolari componenti.

Note

^ Mencuccini, Silvestrini , Pag. 11 .
^ Electric field in "Electricity and Magnetism", R Nave
^ Mencuccini, Silvestrini , Pag. 12 .
^ Mencuccini, Silvestrini , Pag. 14 .
^ Mencuccini, Silvestrini , Pag. 41 .
^ Mencuccini, Silvestrini , Pag. 20 .
^ ^a ^b Mencuccini, Silvestrini , pag. 28 .
^ Mencuccini, Silvestrini , Pag. 54 .
^ Mencuccini, Silvestrini , Pag. 31 .
^ Mencuccini, Silvestrini , Pag. 33 .
^ Mencuccini, Silvestrini , Pag. 107 .
^ ^a ^b Mencuccini, Silvestrini , Pag. 108 .
^ ^a ^b ^c Mencuccini, Silvestrini , Pag. 109 .
^ Mencuccini, Silvestrini , Pag. 110 .
^ Mencuccini, Silvestrini , Pag. 351 .
^ Mencuccini, Silvestrini , Pag. 353 .
^ Mencuccini, Silvestrini , Pag. 361 .
^ Paul G. Huray, Maxwell's Equations , Wiley-IEEE, 2009, p. 205, ISBN 0-470-54276-4 . , Chapter 7, p 205
^ Mencuccini, Silvestrini , Pag. 396 .
^ Mencuccini, Silvestrini , Pag. 397 .
^ Raymond Bonnett, Shane Cloude, An Introduction to Electromagnetic Wave Propagation and Antennas , Taylor & Francis, 1995, p. 16, ISBN 1-85728-241-8 .
^ JC Slater and NH Frank, Electromagnetism , Reprint of 1947 edition, Courier Dover Publications, 1969, p. 84, ISBN 0-486-62263-0 .
^ Mencuccini, Silvestrini , Pag. 398 .
^ Mencuccini, Silvestrini , Pag. 141 .
^ Mencuccini, Silvestrini , Pag. 142 .
^ Mencuccini, Silvestrini , Pag. 143 .
^ Mencuccini, Silvestrini , Pag. 458 .
^ Jackson , Pag. 238 .
^ Mencuccini, Silvestrini , Pag. 147 .
^ Mencuccini, Silvestrini , Pag. 148 .
^ Landau, Lifshits , Pag. 147 .

Bibliografia

Corrado Mencuccini, Vittorio Silvestrini, Fisica II , Napoli, Liguori Editore, 2010, ISBN 978-88-207-1633-2 .
Lev D Landau e Evgenij M. Lifshits , Fisica teorica 2 - Teoria dei campi , Roma, Editori Riuniti Edizioni Mir, 1976, ISBN 88-359-5358-8 .
( EN ) John D Jackson, Classical Electrodynamics , 3rd Edition, Wiley, 1999, ISBN 0-471-30932-X .

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su campo elettrico

Collegamenti esterni

( EN ) Campo elettrico , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.

Controllo di autorità	Thesaurus BNCF 12424 · LCCN ( EN ) sh85041688 · GND ( DE ) 4014211-5 · BNF ( FR ) cb11977320f (data)

Portale Elettromagnetismo

Portale Fisica

[1] Mencuccini, Silvestrini , Pag. 11 .

[hyperphysics.phy-astr.gsu.edu-2] Electric field in "Electricity and Magnetism", R Nave

[3] Mencuccini, Silvestrini , Pag. 12 .

[4] Mencuccini, Silvestrini , Pag. 14 .

[5] Mencuccini, Silvestrini , Pag. 41 .

[6] Mencuccini, Silvestrini , Pag. 20 .

[Mencucci2010-28-7] Mencuccini, Silvestrini , pag. 28 .

[8] Mencuccini, Silvestrini , Pag. 54 .

[9] Mencuccini, Silvestrini , Pag. 31 .

[10] Mencuccini, Silvestrini , Pag. 33 .

[11] Mencuccini, Silvestrini , Pag. 107 .

[pot-12] Mencuccini, Silvestrini , Pag. 108 .

[cond-13] Mencuccini, Silvestrini , Pag. 109 .

[14] Mencuccini, Silvestrini , Pag. 110 .

[15] Mencuccini, Silvestrini , Pag. 351 .

[16] Mencuccini, Silvestrini , Pag. 353 .

[17] Mencuccini, Silvestrini , Pag. 361 .

[18] Paul G. Huray, Maxwell's Equations , Wiley-IEEE, 2009, p. 205, ISBN 0-470-54276-4 . , Chapter 7, p 205

[19] Mencuccini, Silvestrini , Pag. 396 .

[20] Mencuccini, Silvestrini , Pag. 397 .

[Cloude-21] Raymond Bonnett, Shane Cloude, An Introduction to Electromagnetic Wave Propagation and Antennas , Taylor & Francis, 1995, p. 16, ISBN 1-85728-241-8 .

[Slater-22] JC Slater and NH Frank, Electromagnetism , Reprint of 1947 edition, Courier Dover Publications, 1969, p. 84, ISBN 0-486-62263-0 .

[23] Mencuccini, Silvestrini , Pag. 398 .

[24] Mencuccini, Silvestrini , Pag. 141 .

[pol-25] Mencuccini, Silvestrini , Pag. 142 .

[26] Mencuccini, Silvestrini , Pag. 143 .

[27] Mencuccini, Silvestrini , Pag. 458 .

[max-28] Jackson , Pag. 238 .

[29] Mencuccini, Silvestrini , Pag. 147 .

[30] Mencuccini, Silvestrini , Pag. 148 .

[31] Landau, Lifshits , Pag. 147 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]