Curbură

Termenul de curbură indică o serie de concepte geometrice legate între ele, care se referă intuitiv la măsura în care un anumit obiect se abate de la a fi plat. Măsura curburii este definită în moduri diferite în funcție de entitatea geometrică căreia i se aplică. Noțiunea de curbură este baza geometriei diferențiale . Are aplicații notabile în fizică , în special în relativitatea generală .

Curbură intrinsecă și extrinsecă

O cale închisă pe o sferă

Aceeași cale pe avion devine deschisă

Există două tipuri esențiale de curbură:

curbură extrinsecă : este curbura posedată de obiect în raport cu un spațiu plat cu o dimensiune superioară în care este scufundat și poate fi determinată doar prin compararea elementelor obiectului în raport cu elementele spațiului containerului;
curbură intrinsecă : este curbura care poate fi determinată folosind doar operații efectuate pe elemente ale obiectului în sine.

Un exemplu de curbură extrinsecă este cel al unei suprafețe cilindrice în spațiu tridimensional: liniile trasate pe cilindru sunt curbate în comparație cu liniile spațiului în care este scufundat cilindrul. Geometria intrinsecă a cilindrului, pe de altă parte, este plană, deoarece toate axiomele planului euclidian se aplică acestuia.

Pe de altă parte, o sferă are o curbură intrinsecă, care poate fi determinată rămânând în interiorul suprafeței: pe Pământ , o cale care pornește de la polul nord coborând de-a lungul unui meridian , se rotește în unghi drept de-a lungul unei paralele și din nou la unghiuri drepte de-a lungul altui meridian, revine la punctul de plecare. O cale analogă efectuată pe un avion nu trece niciodată prin același punct.

Măsurarea curburii

Circumferința oferă cel mai simplu model de măsurare a curburii (extrinseci): deoarece, într-un plan, curbura $k$ ${\ displaystyle k}$ $k$ intr-un loc $P.$ ${\ displaystyle P}$ $P.$ indică sensibilitatea tangentei în $P.$ ${\ displaystyle P}$ $P.$ să varieze la luarea în considerare a punctelor de lângă $P.$ ${\ displaystyle P}$ $P.$ , circumferințele cu rază mai mare au o curbură mai mică, și invers. Curbura unei curbe $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ este apoi definit ca reciproc al razei de curbură sau echivalent curbura este reciproc al razei cercului oscilant într-un punct:

k:={\frac {1}{R}}.

{\ displaystyle k: = {\ frac {1} {R}}.}

{\ displaystyle k: = {\ frac {1} {R}}.}

Cercul oscilant este un cerc central $ȘI$ ${\ displaystyle E}$ $ȘI$ tangentă la curba care o aproximează „până la al doilea ordin”, adică are aceeași primă și a doua derivată a $\gamma$ ${\ displaystyle \ gamma}$ $\gamă$ în punct (acest loc geometric al centrelor de curbură se numește evoluat al curbei). De sine $P(s)$ ${\ displaystyle P (s)}$ ${\ displaystyle P (s)}$ este o parametrizare a punctelor curbei, atunci centrul cercului osculant este $E(s)=P(s)+R(s)\mathbf {N} (s),$ ${\ displaystyle E (s) = P (s) + R (s) \ mathbf {N} (s),}$ ${\ displaystyle E (s) = P (s) + R (s) \ mathbf {N} (s),}$ unde este $R(s)$ ${\ displaystyle R (s)}$ ${\ displaystyle R (s)}$ este raza cercului oscilant e $\mathbf {N} (s)$ ${\ displaystyle \ mathbf {N} (s)}$ ${\ displaystyle \ mathbf {N} (s)}$ este vectorul unitar normal al curbei în punctul respectiv $P(s).$ ${\ displaystyle P (s).}$ ${\ displaystyle P (s).}$

Reprezentarea unei curbe și a cercului său oscilant , care este tangentă la punct

P.

{\ displaystyle P}

P.

: curbura în

P.

{\ displaystyle P}

P.

este reciprocul razei

r

{\ displaystyle r}

r

a cercului osculant.

Dacă curba este aproape o linie dreaptă, cercul oscilant are o rază mare și curbura este aproape zero (în limită, este zero pentru o linie dreaptă); curburile mari corespund punctelor în care există schimbări puternice de direcție.

Această definiție poate fi extinsă la obiecte mai complexe și mai mari, după cum se indică mai jos.

Curba plană

Același subiect în detaliu: Geometria diferențială a curbelor .

Având o curbă plană $\gamma :P(s)={\big (}x(s),y(s){\big )}$ ${\ displaystyle \ gamma: P (s) = {\ big (} x (s), y (s) {\ big)}}$ ${\ displaystyle \ gamma: P (s) = {\ big (} x (s), y (s) {\ big)}}$ (același raționament se poate face evident în trei dimensiuni) parametrizat prin parametrul arc $s$ ${\ displaystyle s}$ $s$ și sunt ${\hat {\tau }}={\big (}x'(s),y'(s){\big )}$ ${\ displaystyle {\ hat {\ tau}} = {\ big (} x '(s), y' (s) {\ big)}}$ ${\ displaystyle {\ hat {\ tau}} = {\ big (} x '(s), y' (s) {\ big)}}$ Și ${\hat {\tau }}_{0}={\big (}x'(s_{0}),y'(s_{0}){\big )}$ ${\ displaystyle {\ hat {\ tau}} _ {0} = {\ big (} x '(s_ {0}), y' (s_ {0}) {\ big)}}$ ${\ displaystyle {\ hat {\ tau}} _ {0} = {\ big (} x '(s_ {0}), y' (s_ {0}) {\ big)}}$ respectiv versorii tangenți la acesta în puncte $P(s)$ ${\ displaystyle P (s)}$ ${\ displaystyle P (s)}$ Și $P(s_{0})$ ${\ displaystyle P (s_ {0})}$ ${\ displaystyle P (s_ {0})}$ . Spus $\vartheta$ ${\ displaystyle \ vartheta}$ $\ vartheta$ unghiul dintre ele, relația

\displaystyle k_{m}={\frac {\vartheta }{|s_{0}-s|}}

{\ displaystyle \ displaystyle k_ {m} = {\ frac {\ vartheta} {| s_ {0} -s |}}}

{\ displaystyle \ displaystyle k_ {m} = {\ frac {\ vartheta} {| s_ {0} -s |}}}

se numește curbură medie și oferă o indicație a vitezei arcului $P(s)P(s_{0})$ ${\ displaystyle P (s) P (s_ {0})}$ ${\ displaystyle P (s) P (s_ {0})}$ se abate de la direcția tangentei în $P(s)$ ${\ displaystyle P (s)}$ ${\ displaystyle P (s)}$ .

Curba este prezentată în desen

\gamma :P(s)

{\ displaystyle \ gamma: P (s)}

{\ displaystyle \ gamma: P (s)}

și tangențele la acesta în puncte

P(s)

{\ displaystyle P (s)}

{\ displaystyle P (s)}

generic și

P(s_{0})

{\ displaystyle P (s_ {0})}

{\ displaystyle P (s_ {0})}

.

Prin urmare, definește curbura (extrinsecă) limita medie de curbură pentru puncte $P(s_{0})$ ${\ displaystyle P (s_ {0})}$ ${\ displaystyle P (s_ {0})}$ lângă $P(s)$ ${\ displaystyle P (s)}$ ${\ displaystyle P (s)}$ :

k:=\lim _{s_{0}\rightarrow s}{\frac {\vartheta }{|s_{0}-s|}}.

{\ displaystyle k: = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {| s_ {0} -s |}}.}

{\ displaystyle k: = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {| s_ {0} -s |}}.}

Operațional, se poate demonstra că:

\lim _{s_{0}\rightarrow s}{\frac {\vartheta }{|s_{0}-s|}}=\|P''(s)\|.

{\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {| s_ {0} -s |}} = \ | P '' (s) \ |.}

{\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {| s_ {0} -s |}} = \ | P '' (s) \ |.}

Demonstrație

Din moment ce $\lim _{s_{0}\rightarrow s}\vartheta =0$ ${\ displaystyle \ lim _ {s_ {0} \ rightarrow s} \ vartheta = 0}$ ${\ displaystyle \ lim _ {s_ {0} \ rightarrow s} \ vartheta = 0}$ , și apoi $\lim _{s_{0}\rightarrow s}{\frac {\sin \vartheta }{\vartheta }}=1$ ${\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ sin \ vartheta} {\ vartheta}} = 1}$ ${\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ sin \ vartheta} {\ vartheta}} = 1}$ , limita inițială devine:

\lim _{s_{0}\rightarrow s}{\frac {\vartheta }{\left\vert s_{0}-s\right\vert }}{\frac {\sin \vartheta }{\sin \vartheta }}=\lim _{s_{0}\rightarrow s}{\frac {\sin \vartheta }{\left\vert s_{0}-s\right\vert }}=\lim _{s_{0}\rightarrow s}{\frac {\left\Vert {\hat {\tau }}_{0}\times {\hat {\tau }}\right\Vert }{\left\vert s_{0}-s\right\vert }}

{\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {\ left \ vert s_ {0} -s \ right \ vert}} {\ frac {\ sin \ vartheta} {\ sin \ vartheta}} = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ sin \ vartheta} {\ left \ vert s_ {0} -s \ right \ vert}} = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ left \ Vert {\ hat {\ tau}} _ {0} \ times {\ hat {\ tau}} \ right \ Vert} {\ left \ vert s_ {0 } -s \ right \ vert}}}

{\ displaystyle \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ vartheta} {\ left \ vert s_ {0} -s \ right \ vert}} {\ frac {\ sin \ vartheta} {\ sin \ vartheta}} = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ sin \ vartheta} {\ left \ vert s_ {0} -s \ right \ vert}} = \ lim _ {s_ {0} \ rightarrow s} {\ frac {\ left \ Vert {\ hat {\ tau}} _ {0} \ times {\ hat {\ tau}} \ right \ Vert} {\ left \ vert s_ {0 } -s \ right \ vert}}}

,

deoarece unitățile vectoriale au un modul unitar ( $\left\Vert {\vec {u}}\times {\vec {v}}\right\Vert =\left\Vert {\vec {u}}\right\Vert \,\left\Vert {\vec {v}}\right\Vert \,\sin \vartheta$ ${\ displaystyle \ left \ Vert {\ vec {u}} \ times {\ vec {v}} \ right \ Vert = \ left \ Vert {\ vec {u}} \ right \ Vert \, \ left \ Vert { \ vec {v}} \ right \ Vert \, \ sin \ vartheta}$ ${\ displaystyle \ left \ Vert {\ vec {u}} \ times {\ vec {v}} \ right \ Vert = \ left \ Vert {\ vec {u}} \ right \ Vert \, \ left \ Vert { \ vec {v}} \ right \ Vert \, \ sin \ vartheta}$ ). Prin formula lui Taylor cu restul lui Peano avem variabila $the$ ${\ displaystyle i}$ $the$ -th poate fi aproximat ca. $x_{i}'(s_{0})=x_{i}'(s)+x_{i}''(s)(s_{0}-s)+o(s_{0}-s)$ ${\ displaystyle x_ {i} '(s_ {0}) = x_ {i}' (s) + x_ {i} '' (s) (s_ {0} -s) + o (s_ {0} -s )}}$ ${\ displaystyle x_ {i} '(s_ {0}) = x_ {i}' (s) + x_ {i} '' (s) (s_ {0} -s) + o (s_ {0} -s )}}$ , iar apoi raportul anterior devine:

{\frac {\left\Vert {\hat {\tau }}_{0}\times {\hat {\tau }}\right\Vert }{\left\vert s_{0}-s\right\vert }}={\frac {\left\Vert \det {\begin{bmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\x'(s_{0})&y'(s_{0})&0\\x'(s)&y'(s)&0\end{bmatrix}}\right\Vert }{\left\vert s_{0}-s\right\vert }}={\frac {\left\vert x'(s_{0})y'(s)-y'(s_{0})x'(s)\right\vert }{\left\vert s_{0}-s\right\vert }}=\left\vert x''(s)y'(s)-y''(s)x'(s)+\left[y'(s)-x'(s)\right]o(1)\right\vert

{\ displaystyle {\ frac {\ left \ Vert {\ hat {\ tau}} _ {0} \ times {\ hat {\ tau}} \ right \ Vert} {\ left \ vert s_ {0} -s \ dreapta \ vert}} = {\ frac {\ left \ Vert \ det {\ begin {bmatrix} {\ hat {i}} & {\ hat {j}} & {\ hat {k}} \\ x '( s_ {0}) & y '(s_ {0}) & 0 \\ x' (s) & y '(s) & 0 \ end {bmatrix}} \ right \ Vert} {\ left \ vert s_ {0 } -s \ right \ vert}} = {\ frac {\ left \ vert x '(s_ {0}) y' (s) -y '(s_ {0}) x' (s) \ right \ vert} {\ left \ vert s_ {0} -s \ right \ vert}} = \ left \ vert x '' (s) y '(s) -y' '(s) x' (s) + \ left [y '(s) -x' (s) \ right] sau (1) \ right \ vert}

{\ displaystyle {\ frac {\ left \ Vert {\ hat {\ tau}} _ {0} \ times {\ hat {\ tau}} \ right \ Vert} {\ left \ vert s_ {0} -s \ dreapta \ vert}} = {\ frac {\ left \ Vert \ det {\ begin {bmatrix} {\ hat {i}} & {\ hat {j}} & {\ hat {k}} \\ x '( s_ {0}) & y '(s_ {0}) & 0 \\ x' (s) & y '(s) & 0 \ end {bmatrix}} \ right \ Vert} {\ left \ vert s_ {0 } -s \ right \ vert}} = {\ frac {\ left \ vert x '(s_ {0}) y' (s) -y '(s_ {0}) x' (s) \ right \ vert} {\ left \ vert s_ {0} -s \ right \ vert}} = \ left \ vert x '' (s) y '(s) -y' '(s) x' (s) + \ left [y '(s) -x' (s) \ right] sau (1) \ right \ vert}

.

În cele din urmă, punând totul la limită pentru $s_{0}\rightarrow s$ ${\ displaystyle s_ {0} \ rightarrow s}$ ${\ displaystyle s_ {0} \ rightarrow s}$ :

\left\vert x''(s)y'(s)-y''(s)x'(s)\right\vert =\left\Vert \det {\begin{bmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\x''(s)&y''(s)&0\\x'(s)&y'(s)&0\end{bmatrix}}\right\Vert =\left\Vert P''(s)\times {\hat {\tau }}\right\Vert =\left\Vert P''(s)\right\Vert \,\left\Vert {\hat {\tau }}\right\Vert \,\sin 90^{\circ }=\left\Vert P''(s)\right\Vert

{\ displaystyle \ left \ vert x '' (s) y '(s) -y' '(s) x' (s) \ right \ vert = \ left \ Vert \ det {\ begin {bmatrix} {\ hat {i}} & {\ hat {j}} & {\ hat {k}} \\ x '' (s) & y '' (s) & 0 \\ x '(s) & y' (s) & 0 \ end {bmatrix}} \ right \ Vert = \ left \ Vert P '' (s) \ times {\ hat {\ tau}} \ right \ Vert = \ left \ Vert P '' (s) \ right \ Vert \, \ left \ Vert {\ hat {\ tau}} \ right \ Vert \, \ sin 90 ^ {\ circ} = \ left \ Vert P '' (s) \ right \ Vert}

{\ displaystyle \ left \ vert x '' (s) y '(s) -y' '(s) x' (s) \ right \ vert = \ left \ Vert \ det {\ begin {bmatrix} {\ hat {i}} & {\ hat {j}} & {\ hat {k}} \\ x '' (s) & y '' (s) & 0 \\ x '(s) & y' (s) & 0 \ end {bmatrix}} \ right \ Vert = \ left \ Vert P '' (s) \ times {\ hat {\ tau}} \ right \ Vert = \ left \ Vert P '' (s) \ right \ Vert \, \ left \ Vert {\ hat {\ tau}} \ right \ Vert \, \ sin 90 ^ {\ circ} = \ left \ Vert P '' (s) \ right \ Vert}

,

și, prin urmare, afirmația inițială ( QED ).

Prin urmare, o definiție alternativă a curburii poate fi: $k=\left\|{\frac {d\mathbf {T} }{ds}}\right\|$ ${\ displaystyle k = \ left \ | {\ frac {d \ mathbf {T}} {ds}} \ right \ |}$ ${\ displaystyle k = \ left \ | {\ frac {d \ mathbf {T}} {ds}} \ right \ |}$ , unde este $\mathbf {T}$ ${\ displaystyle \ mathbf {T}}$ ${\ displaystyle \ mathbf {T}}$ este vectorul tangent la curbă (rețineți cum vectorul tangent, dacă este parametrizat cu $s$ ${\ displaystyle s}$ $s$ , are deja formă unitară).

Pentru a calcula curbura (în orice dimensiune) se pot utiliza următoarele formule:

k={\frac {\left\|\displaystyle {\frac {d\mathbf {T} }{dt}}\right\|}{{\big \|}P'(t){\big \|}}}\,\,\,\,\,,\,\,\,\,\,k={\frac {\left\|P'(t)\times P''(t)\right\|}{{\big \|}P'(t){\big \|}^{3}}}

{\ displaystyle k = {\ frac {\ left \ | \ displaystyle {\ frac {d \ mathbf {T}} {dt}} \ right \ |} {{\ big \ |} P '(t) {\ big \ |}}} \, \, \, \, \ ,, \, \, \, \, \, k = {\ frac {\ left \ | P '(t) \ times P' '(t) \ dreapta \ |} {{\ big \ |} P '(t) {\ big \ |} ^ {3}}}}

{\ displaystyle k = {\ frac {\ left \ | \ displaystyle {\ frac {d \ mathbf {T}} {dt}} \ right \ |} {{\ big \ |} P '(t) {\ big \ |}}} \, \, \, \, \ ,, \, \, \, \, \, k = {\ frac {\ left \ | P '(t) \ times P' '(t) \ dreapta \ |} {{\ big \ |} P '(t) {\ big \ |} ^ {3}}}}

.

Demonstrația 1

Un vector generic normal la curbă $P(t)$ ${\ displaystyle P (t)}$ $P (t)$ în formă parametrică este ${\frac {d\mathbf {T} }{dt}}={\frac {d\mathbf {T} }{ds}}{\frac {ds}{dt}}={\frac {d\mathbf {T} }{ds}}\left\Vert P'(t)\right\Vert$ ${\ displaystyle {\ frac {d \ mathbf {T}} {dt}} = {\ frac {d \ mathbf {T}} {ds}} {\ frac {ds} {dt}} = {\ frac {d \ mathbf {T}} {ds}} \ left \ Vert P '(t) \ right \ Vert}$ ${\ displaystyle {\ frac {d \ mathbf {T}} {dt}} = {\ frac {d \ mathbf {T}} {ds}} {\ frac {ds} {dt}} = {\ frac {d \ mathbf {T}} {ds}} \ left \ Vert P '(t) \ right \ Vert}$ ; de fapt, ultima egalitate se obține derivând cu privire la $t$ ${\ displaystyle t}$ $t$ parametrul lungimii arcului $s(t)=\int \left\Vert P'(t)\right\Vert \,dt$ ${\ displaystyle s (t) = \ int \ left \ Vert P '(t) \ right \ Vert \, dt}$ ${\ displaystyle s (t) = \ int \ left \ Vert P '(t) \ right \ Vert \, dt}$ . Prin inserarea acestei relații în definiția anterioară a curburii rezultă că: $k=\left\Vert {\frac {d\mathbf {T} }{ds}}\right\Vert ={\frac {\left\Vert {\cfrac {d\mathbf {T} }{dt}}\right\Vert }{\left\Vert P'(t)\right\Vert }}$ ${\ displaystyle k = \ left \ Vert {\ frac {d \ mathbf {T}} {ds}} \ right \ Vert = {\ frac {\ left \ Vert {\ cfrac {d \ mathbf {T}} {dt }} \ right \ Vert} {\ left \ Vert P '(t) \ right \ Vert}}}$ ${\ displaystyle k = \ left \ Vert {\ frac {d \ mathbf {T}} {ds}} \ right \ Vert = {\ frac {\ left \ Vert {\ cfrac {d \ mathbf {T}} {dt }} \ right \ Vert} {\ left \ Vert P '(t) \ right \ Vert}}}$ (QED).

Demonstrația 2

Pentru a doua formulă, însă, prin unirea ecuațiilor ${\frac {ds}{dt}}=\left\Vert P'(t)\right\Vert$ ${\ displaystyle {\ frac {ds} {dt}} = \ left \ Vert P '(t) \ right \ Vert}$ ${\ displaystyle {\ frac {ds} {dt}} = \ left \ Vert P '(t) \ right \ Vert}$ Și $\mathbf {T} ={\frac {P'(t)}{\left\Vert P'(t)\right\Vert }}$ ${\ displaystyle \ mathbf {T} = {\ frac {P '(t)} {\ left \ Vert P' (t) \ right \ Vert}}}$ ${\ displaystyle \ mathbf {T} = {\ frac {P '(t)} {\ left \ Vert P' (t) \ right \ Vert}}}$ (versor tangent) obținem $P'(t)={\frac {ds}{dt}}\mathbf {T}$ ${\ displaystyle P '(t) = {\ frac {ds} {dt}} \ mathbf {T}}$ ${\ displaystyle P '(t) = {\ frac {ds} {dt}} \ mathbf {T}}$ . Pe de altă parte, vectorul normal, fiind derivatul vectorului tangent, se dovedește a fi $P''(t)={\frac {P'(t)}{dt}}={\frac {d^{2}s}{{dt}^{2}}}\mathbf {T} +{\frac {ds}{dt}}{\frac {d\mathbf {T} }{dt}}$ ${\ displaystyle P '' (t) = {\ frac {P '(t)} {dt}} = {\ frac {d ^ {2} s} {{dt} ^ {2}}} \ mathbf {T } + {\ frac {ds} {dt}} {\ frac {d \ mathbf {T}} {dt}}}$ ${\ displaystyle P '' (t) = {\ frac {P '(t)} {dt}} = {\ frac {d ^ {2} s} {{dt} ^ {2}}} \ mathbf {T } + {\ frac {ds} {dt}} {\ frac {d \ mathbf {T}} {dt}}}$ . Acum înmulțim vectorial vectorii tangenți și normali dintre ei: $P'(t)\times P''(t)={\frac {ds}{dt}}{\frac {d^{2}s}{{dt}^{2}}}\left(\mathbf {T} \times \mathbf {T} \right)+\left({\frac {ds}{dt}}\right)^{2}\left(\mathbf {T} \times {\frac {d\mathbf {T} }{dt}}\right)$ ${\ displaystyle P '(t) \ times P' '(t) = {\ frac {ds} {dt}} {\ frac {d ^ {2} s} {{dt} ^ {2}}} \ left (\ mathbf {T} \ times \ mathbf {T} \ right) + \ left ({\ frac {ds} {dt}} \ right) ^ {2} \ left (\ mathbf {T} \ times {\ frac {d \ mathbf {T}} {dt}} \ right)}$ ${\ displaystyle P '(t) \ times P' '(t) = {\ frac {ds} {dt}} {\ frac {d ^ {2} s} {{dt} ^ {2}}} \ left (\ mathbf {T} \ times \ mathbf {T} \ right) + \ left ({\ frac {ds} {dt}} \ right) ^ {2} \ left (\ mathbf {T} \ times {\ frac {d \ mathbf {T}} {dt}} \ right)}$ ; întrucât produsul vector al unui vector în sine este zero e $\mathbf {T}$ ${\ displaystyle \ mathbf {T}}$ ${\ displaystyle \ mathbf {T}}$ Și ${\frac {d\mathbf {T} }{dt}}$ ${\ displaystyle {\ frac {d \ mathbf {T}} {dt}}}$ ${\ displaystyle {\ frac {d \ mathbf {T}} {dt}}}$ sunt perpendiculare (derivata versorului tangent este pentru fiecare efect un vector normal) obținem: $\left\Vert P'(t)\times P''(t)\right\Vert =\left({\frac {ds}{dt}}\right)^{2}\left\Vert {\frac {d\mathbf {T} }{dt}}\right\Vert =\left\Vert P'(t)\right\Vert ^{2}\left\Vert {\frac {d\mathbf {T} }{dt}}\right\Vert$ ${\ displaystyle \ left \ Vert P '(t) \ times P' '(t) \ right \ Vert = \ left ({\ frac {ds} {dt}} \ right) ^ {2} \ left \ Vert { \ frac {d \ mathbf {T}} {dt}} \ right \ Vert = \ left \ Vert P '(t) \ right \ Vert ^ {2} \ left \ Vert {\ frac {d \ mathbf {T} } {dt}} \ right \ Vert}$ ${\ displaystyle \ left \ Vert P '(t) \ times P' '(t) \ right \ Vert = \ left ({\ frac {ds} {dt}} \ right) ^ {2} \ left \ Vert { \ frac {d \ mathbf {T}} {dt}} \ right \ Vert = \ left \ Vert P '(t) \ right \ Vert ^ {2} \ left \ Vert {\ frac {d \ mathbf {T} } {dt}} \ right \ Vert}$ . În sfârșit, din moment ce $k={\frac {\left\Vert {\cfrac {d\mathbf {T} }{dt}}\right\Vert }{\left\Vert P'(t)\right\Vert }}$ ${\ displaystyle k = {\ frac {\ left \ Vert {\ cfrac {d \ mathbf {T}} {dt}} \ right \ Vert} {\ left \ Vert P '(t) \ right \ Vert}}}$ ${\ displaystyle k = {\ frac {\ left \ Vert {\ cfrac {d \ mathbf {T}} {dt}} \ right \ Vert} {\ left \ Vert P '(t) \ right \ Vert}}}$ , da $k={\frac {\left\Vert P'(t)\times P''(t)\right\Vert }{\left\Vert P'(t)\right\Vert ^{3}}}$ ${\ displaystyle k = {\ frac {\ left \ Vert P '(t) \ times P' '(t) \ right \ Vert} {\ left \ Vert P' (t) \ right \ Vert ^ {3}} }}$ ${\ displaystyle k = {\ frac {\ left \ Vert P '(t) \ times P' '(t) \ right \ Vert} {\ left \ Vert P' (t) \ right \ Vert ^ {3}} }}$ (QED).

Formule utile

Următoarele formule pot fi utilizate pentru calculul explicit al curburii:

Curba în formă parametrică $\gamma (t)={\big (}x(t),y(t){\big )}$ ${\ displaystyle \ gamma (t) = {\ big (} x (t), y (t) {\ big)}}$ ${\ displaystyle \ gamma (t) = {\ big (} x (t), y (t) {\ big)}}$ :
$k={\frac {\left|{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}\right|}{({{\dot {x}}^{2}+{\dot {y}}^{2})}^{\frac {3}{2}}}}$ ${\ displaystyle k = {\ frac {\ left | {\ dot {x}} {\ ddot {y}} - {\ dot {y}} {\ ddot {x}} \ right |} {({{\ punct {x}} ^ {2} + {\ dot {y}} ^ {2})} ^ {\ frac {3} {2}}}}}$ ${\ displaystyle k = {\ frac {\ left | {\ dot {x}} {\ ddot {y}} - {\ dot {y}} {\ ddot {x}} \ right |} {({{\ punct {x}} ^ {2} + {\ dot {y}} ^ {2})} ^ {\ frac {3} {2}}}}}$ ,

unde punctele de deasupra variabilelor reprezintă derivatele în raport cu parametrul

t

{\ displaystyle t}

t

. Se derivă direct din

k={\frac {\left\|P'(t)\times P''(t)\right\|}{{\big \|}P'(t){\big \|}^{3}}}

{\ displaystyle k = {\ frac {\ left \ | P '(t) \ times P' '(t) \ right \ |} {{\ big \ |} P' (t) {\ big \ |} ^ {3}}}}

{\ displaystyle k = {\ frac {\ left \ | P '(t) \ times P' '(t) \ right \ |} {{\ big \ |} P' (t) {\ big \ |} ^ {3}}}}

amintind produsul vector în formă matricială.

Curba formei polare $r=r(\vartheta )$ ${\ displaystyle r = r (\ vartheta)}$ ${\ displaystyle r = r (\ vartheta)}$ :
$k={\frac {{\big |}r^{2}+2{r'}^{2}-rr''{\big |}}{(r^{2}+{r'}^{2})^{\frac {3}{2}}}}$ ${\ displaystyle k = {\ frac {{\ big |} r ^ {2} +2 {r '} ^ {2} -rr' '{\ big |}} {(r ^ {2} + {r' } ^ {2}) ^ {\ frac {3} {2}}}}}$ ${\ displaystyle k = {\ frac {{\ big |} r ^ {2} +2 {r '} ^ {2} -rr' '{\ big |}} {(r ^ {2} + {r' } ^ {2}) ^ {\ frac {3} {2}}}}}$ ,

unde derivatele sunt făcute în ceea ce privește

\vartheta

{\ displaystyle \ vartheta}

\ vartheta

. De asemenea, poate fi considerat un caz particular al precedentului dacă luăm în considerare o curbă polară exprimată în formă parametrică

{\begin{cases}\phi (\vartheta )=r(\vartheta )\cos {\vartheta }\\\varphi (\vartheta )=r(\vartheta )\sin {\vartheta }\end{cases}}

{\ displaystyle {\ begin {cases} \ phi (\ vartheta) = r (\ vartheta) \ cos {\ vartheta} \\\ varphi (\ vartheta) = r (\ vartheta) \ sin {\ vartheta} \ end { cazuri}}}

{\ displaystyle {\ begin {cases} \ phi (\ vartheta) = r (\ vartheta) \ cos {\ vartheta} \\\ varphi (\ vartheta) = r (\ vartheta) \ sin {\ vartheta} \ end { cazuri}}}

.

Curba sub formă implicită $f(x,y)=0$ ${\ displaystyle f (x, y) = 0}$ $f (x, y) = 0$ :
$k=\left|\nabla \cdot \left({\frac {\nabla f}{\|\nabla f\|}}\right)\right|$ ${\ displaystyle k = \ left | \ nabla \ cdot \ left ({\ frac {\ nabla f} {\ | \ nabla f \ |}} \ right) \ right |}$ $k = \ left | \ nabla \ cdot \ left ({\ frac {\ nabla f} {\ | \ nabla f \ |}} \ right) \ right |$ ,

adică curbura este divergența direcției gradientului de

f

{\ displaystyle f}

f

.

Curba în formă explicită $y=f(x)$ ${\ displaystyle y = f (x)}$ $y = f (x)$ :
$k=\displaystyle {\frac {|y''|}{\left(1+{y'}^{2}\right)^{\frac {3}{2}}}}$ ${\ displaystyle k = \ displaystyle {\ frac {| y '' |} {\ left (1+ {y '} ^ {2} \ right) ^ {\ frac {3} {2}}}}}$ ${\ displaystyle k = \ displaystyle {\ frac {| y '' |} {\ left (1+ {y '} ^ {2} \ right) ^ {\ frac {3} {2}}}}}$ ,

care se poate obține din aceasta în formă parametrică prin plasare

t=x

{\ displaystyle t = x}

{\ displaystyle t = x}

. Dacă panta funcției este neglijabilă în raport cu unitatea, atunci se poate utiliza aproximarea

k\approx y^{\prime \prime }

{\ displaystyle k \ approx y ^ {\ prime \ prime}}

k \ approx y ^ {{\ prime \ prime}}

.

Curba în spațiu

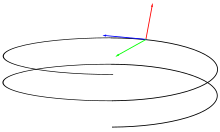
Același subiect în detaliu: Geometria diferențială a curbelor .

Triedrul Frenet al unei spirale

Comportamentul unei curbe în spațiu $\mathbb {R} ^{3}$ ${\ displaystyle \ mathbb {R} ^ {3}}$ $\ mathbb {R} ^ 3$ poate fi descris prin intermediul triadei Frenet , un sistem de referință format din trei vectori unitari . Sunt asociate două cantități scalare :

curbura , care este modulul vectorului normal la curbă și extinde conceptul de curbură definit pentru o curbă plană;
torsiunea , care măsoară cât de mult curba tinde să se abată de la planul osculant (planul care aproximează curba până la ordinul doi și care este determinat de primii doi vectori ai triplului Frenet); o curbă plană are deci torsiune zero.

Vectorul de curbură al proiecției ortogonale a curbei pe planul său tangent se numește vectorul de curbură geodezică ; modulul său, numit curbură geodezică, exprimă o altă măsură de curbură, înțeleasă ca deviația curbei în raport cu arcul de lungime minimă dintre două puncte învecinate. Curbele cu curbură geodezică zero se numesc geodezice .

Curba în n dimensiuni

Același subiect în detaliu: Geometria diferențială a curbelor .

În cel mai general caz, o curbă cufundată într-un spațiu $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ este descris de $n$ ${\ displaystyle n}$ $n$ vectori ortonormali (sistem Frenet generalizat)

{\vec {e}}_{1}(t),\ldots ,{\vec {e}}_{n}(t)

{\ displaystyle {\ vec {e}} _ {1} (t), \ ldots, {\ vec {e}} _ {n} (t)}

{\ vec e} _ {1} (t), \ ldots, {\ vec e} _ {n} (t)

,

la care sunt asociate $n-1$ ${\ displaystyle n-1}$ $n - 1$ curburi generalizate definite de

\chi _{i}(t)={\frac {\langle {\vec {e}}_{i}\,'(t),{\vec {e}}_{i+1}(t)\rangle }{|f'(t)|}}

{\ displaystyle \ chi _ {i} (t) = {\ frac {\ langle {\ vec {e}} _ {i} \, '(t), {\ vec {e}} _ {i + 1} (t) \ rangle} {| f '(t) |}}}

\ chi _ {i} (t) = {\ frac {\ langle {\ vec e} _ {i} \, '(t), {\ vec e} _ {{i + 1}} (t) \ rangle } {| f '(t) |}}

.

Suprafața în spațiu

Același subiect în detaliu: curbură principală , curbură gaussiană și curbură medie .

Un hiperboloid , un cilindru și o sferă : acestea sunt suprafețe cu curbură gaussiană (respectiv) negativă, nulă și pozitivă.

Pe o suprafață bidimensională, curbura variază în funcție de direcția în care este calculată. Cu toate acestea, este posibil să se măsoare pornind de la doar câteva direcții semnificative.

Având în vedere un punct $P.$ ${\ displaystyle P}$ $P.$ din suprafață, se iau în considerare toate planurile care trec prin normalul care intră în suprafață $P.$ ${\ displaystyle P}$ $P.$ : intersecția fiecărui plan cu suprafața determină o curbă plană a cărei curbură poate fi calculată, cu următoarea convenție: curbura este pozitivă dacă curba deviază în aceeași direcție ca cea normală, negativă în cazul opus. Valorile maxime și minime ale curburii astfel obținute se numesc curburi principale , direcțiile respective fiind numite direcții principale . Determinarea direcțiilor principale poate fi efectuată cu ajutorul operatorului Weingarten .

Având în vedere cele două curburi principale $k_{1}$ ${\ displaystyle k_ {1}}$ $k_1$ Și $k_{2}$ ${\ displaystyle k_ {2}}$ $k_2$ , este posibil să se definească două măsuri diferite de curbură: curbura Gaussiană și curbura medie .

Curbura Gaussiană este dată de produsul celor două curburi principale, $k_{G}=k_{1}k_{2}$ ${\ displaystyle k_ {G} = k_ {1} k_ {2}}$ $k_ {G} = k_ {1} k_ {2}$ . Dacă cele două curburi principale au același semn, curbura Gauss este pozitivă și indică faptul că suprafața este local convexă (ca în cazul sferei); dacă în schimb au semn opus, curbura este negativă și suprafața are forma unei șe (ca în cazul unui hiperboloid ). Punctele de pe suprafața în care curbura Gauss este pozitivă se numesc puncte eliptice , punctele în care este negativă se numesc puncte hiperbolice . Dacă într-un punct al suprafeței doar una dintre cele două curburi principale este egală cu zero, curbura Gaussiană este zero și punctul se numește punct parabolic (ca în cazul cilindrului); dacă ambele curburi principale sunt zero, punctul se numește punct plan (acesta este cazul planului).

După cum a demonstrat Gauss în Theorema Egregium , curbura Gauss nu depinde de fapt de scufundarea suprafeței într-un spațiu mai mare și poate fi definită folosind doar caracteristici ale suprafeței în sine, de exemplu în modul următor: distanța dintre două puncte pe suprafață este lungimea minimă dintre cele ale arcurilor care unesc cele două puncte rămase pe suprafață; o circumferință la suprafață este locusul punctelor la o distanță fixă $R.$ ${\ displaystyle R}$ $R.$ dintr-un punct $P.$ ${\ displaystyle P}$ $P.$ . Curbura Gaussiană poate fi calculată ca:

k_{G}=\lim _{R\rightarrow 0}{\big (}2\pi R-{\mbox{C}}(R){\big )}\cdot {\frac {3}{\pi R^{3}}}

{\ displaystyle k_ {G} = \ lim _ {R \ rightarrow 0} {\ big (} 2 \ pi R - {\ mbox {C}} (R) {\ big)} \ cdot {\ frac {3} {\ pi R ^ {3}}}}

{\ displaystyle k_ {G} = \ lim _ {R \ rightarrow 0} {\ big (} 2 \ pi R - {\ mbox {C}} (R) {\ big)} \ cdot {\ frac {3} {\ pi R ^ {3}}}}

,

unde este ${\mbox{C}}(R)$ ${\ displaystyle {\ mbox {C}} (R)}$ ${\ mbox {C}} (R)$ este lungimea circumferinței la suprafață. Pentru un spațiu plat, ${\mbox{C}}(R)=2\pi R$ ${\ displaystyle {\ mbox {C}} (R) = 2 \ pi R}$ ${\ mbox {C}} (R) = 2 \ pi R$ iar curbura Gauss este zero.

Direcțiile principale într-un cilindru

Curbura medie este media aritmetică a celor două curburi principale, $k_{m}={\frac {k_{1}+k_{2}}{2}}$ ${\ displaystyle k_ {m} = {\ frac {k_ {1} + k_ {2}} {2}}}$ $k_ {m} = {\ frac {k_ {1} + k_ {2}} {2}}$ . Depinde de spațiul în care este scufundată suprafața și, prin urmare, este o curbură extrinsecă. Curbura medie este strâns legată de problemele minime de suprafață: fiecare suprafață minimă are o curbură medie egală cu zero.

Ca exemplu de calcul al curburii, să luăm în considerare un cilindru de rază $R.$ ${\ displaystyle R}$ $R.$ : cele două direcții principale sunt paralele și perpendiculare pe axa cilindrului; se aplică curburile respective $k_{1}=0$ ${\ displaystyle k_ {1} = 0}$ $k_ {1} = 0$ Și $k_{2}={\frac {1}{R}}$ ${\ displaystyle k_ {2} = {\ frac {1} {R}}}$ $k_ {2} = {\ frac {1} {R}}$ . Curbura Gaussiană se menține $k_{1}k_{2}=0$ ${\ displaystyle k_ {1} k_ {2} = 0}$ $k_ {1} k_ {2} = 0$ , prin urmare geometria intrinsecă a cilindrului este plană; curbura medie este valabilă în schimb ${\frac {k_{1}+k_{2}}{2}}={\frac {1}{2R}}$ ${\ displaystyle {\ frac {k_ {1} + k_ {2}} {2}} = {\ frac {1} {2R}}}$ ${\ frac {k_ {1} + k_ {2}} {2}} = {\ frac {1} {2R}}$ .

Soi diferențiat

Transport paralel al unui vector de-a lungul unei căi închise pe o sferă: la sfârșitul căii

LA Nu. B. LA

{\ displaystyle ANBA}

ANBA

vectorul este deviat datorită curburii sferei în sine.

O varietate diferențiată poate fi înzestrată cu o altă structură care determină metrica sa (varietatea Riemanniană sau pseudo-Riemanniană) și, cu aceasta, curbura sa; această structură este definită de tensorul de curbură Riemann .

Obiectul astfel definit este strâns legat de o definiție intrinsecă a curburii, numită transport paralel : se realizează prin tragerea unui vector punct cu punct de-a lungul unei căi închise conținute în colector, astfel încât direcția vectorului (referită la colector și nu la spațiul care îl conține) nu se schimbă. După ce a acoperit o revoluție completă, vectorul nu mai coincide cu vectorul original, ci este deviat de o cantitate care depinde atât de aria suprafeței delimitate de calea închisă, cât și de curbura intrinsecă a suprafeței în sine ( pentru suprafețele plane deviația nu este nimic).

Folosind notația lui Einstein pentru tensori , cantitatea de variație pe care o suferă un vector pentru un transport paralel de-a lungul marginii suprafeței $\Sigma$ ${\ displaystyle \ Sigma}$ $\ Sigma$ este dat de:

\Delta A^{\mu }={\frac {1}{2}}\int _{\Sigma }{dS^{\beta \sigma }R_{\nu \beta \sigma }^{\mu }A^{\nu }}

{\ displaystyle \ Delta A ^ {\ mu} = {\ frac {1} {2}} \ int _ {\ Sigma} {dS ^ {\ beta \ sigma} R _ {\ nu \ beta \ sigma} ^ { \ mu} A ^ {\ nu}}}

\ Delta A ^ {\ mu} = {\ frac {1} {2}} \ int _ {\ Sigma} {dS ^ {{\ beta \ sigma}} R _ {{\ nu \ beta \ sigma}} ^ {\ mu} A ^ {\ nu}}

.

Curbura spațiului fizic și a gravitației

Același subiect în detaliu: relativitatea generală .

Reprezentarea celor trei destine posibile ale Universului conform teoriei relativității: de sus, univers finit cu curbură pozitivă, univers infinit cu curbură negativă, univers plat cu curbură zero.

Conform teoriei relativității generale , gravitația este o expresie a curburii spațiu-timpului , o varietate pseudo-riemanniană . La rândul său, curbura este determinată de distribuția în spațiu a masei , a energiei și a presiunii , în conformitate cu ecuația câmpului lui Einstein :

R_{\mu \nu }-{1 \over 2}g_{\mu \nu }R+\Lambda g_{\mu \nu }={\frac {8\pi G}{c^{4}}}T_{\mu \nu }

{\ displaystyle R _ {\ mu \ nu} - {1 \ over 2} g _ {\ mu \ nu} R + \ Lambda g _ {\ mu \ nu} = {\ frac {8 \ pi G} {c ^ {4}}} T _ {\ mu \ nu}}

R _ {{\ mu \ nu}} - {1 \ over 2} g _ {{\ mu \ nu}} R + \ Lambda g _ {{\ mu \ nu}} = {\ frac {8 \ pi G } {c ^ {4}}} T _ {{\ mu \ nu}}

,

unde este $R.$ ${\ displaystyle R}$ $R.$ este tensorul Ricci , o contracție a tensorului Riemann, $\Lambda$ ${\ displaystyle \ Lambda}$ $\ Lambda$ este constanta cosmologică , $g$ ${\ displaystyle g}$ $g$ este metrica spațiu-timp, $T.$ ${\ displaystyle T}$ $T.$ este tensorul energetic al impulsului .

Notă

Bibliografie

( EN ) Bernard F. Schutz , Multiple curbe , în Bernard F. Schutz, Un prim curs de relativitate generală . Cambridge University Press, 1985. ISBN 0-521-27703-5
Calogero Vinti, Lecții de analiză matematică (cu exerciții efectuate și propuse) , Volumul II, Galeno Editrice - Perugia, 1983.