Funcția Cantor

În matematică , funcția Cantor (numită uneori funcția Cantor-Vitali sau scara diavolului ) este un exemplu de funcție continuă și în creștere , în ciuda faptului că are derivată zero în aproape toate punctele fiind constantă în toate subintervalele de [0,1] care nu conțin puncte din setul Cantor . Intuitiv, este o scară cu trepte infinite, toate cu o pantă zero, dar la înălțimi crescând progresiv, astfel încât panta medie este încă egală cu 1.

Funcția Cantor este o scară cu trepte infinite de pantă zero, dar cu înălțime în creștere progresivă: acest desen arată o aproximare.

Definiție

Cu elementele de bază

Funcția Cantor f : [0, 1] → [0, 1] este definită după cum urmează:

Scriem fiecare număr x în [0, 1] în baza trei . Cu această notație, 1/3 este scris ca 0,1 ₃ și 2/3 este scris ca 0,2 ₃ . Observăm că unele numere raționale pot avea două scrieri diferite, de exemplu 1/3 este, de asemenea, scris ca 0,0222 ... ₃ (acest fapt este valabil și în baza 10: de fapt, 0,1 este scris și ca 0,09999 ...). Alegem, atunci când este posibil, o notație care nu conține numărul „1”.
Înlocuim prima apariție a cifrei "1" cu un "2" și toate cifrele ulterioare cu "0".
Înlocuim toate cifrele „2” cu „1”.
Interpretăm rezultatul ca un număr binar. Acest rezultat este f ( x ).

De exemplu:

1/4 = 0,02020202 ... ₃ devine 0,01010101 ... ₂ = 1/3. Deci f (1/4) = (1/3).
1/5 = 0,01210121 ... ₃ , în pasul 2 devine 0,02000000 ..., deci 0,01000000 ... ₂ = 1/4. Deci f (1/5) = 1/4.

Ca limită a unei succesiuni

Funcția poate fi definită și ca limita unei succesiuni de funcții definite în [0,1], construite în acest fel:

Este $f_{0}(x)=x$ ${\ displaystyle f_ {0} (x) = x}$ $f _ {{0}} (x) = x$ ;
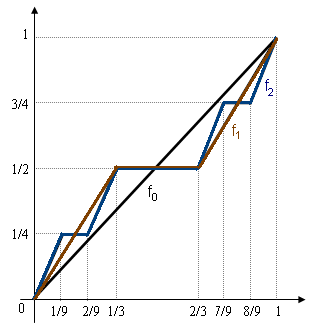
Este $f_{n}(x)$ ${\ displaystyle f_ {n} (x)}$ $f _ {{n}} (x)$ o funcție crescătoare al cărei grafic este poligonalul sugerat în figura din lateral, având $2^{n+1}-1$ ${\ displaystyle 2 ^ {n + 1} -1}$ $2 ^ {{n + 1}} - 1$ laturi: 2 ⁿ laturi sunt oblic ale coeficientului unghiular (3/2) ⁿ și 2 ⁿ -1 laturi sunt orizontale, fiecare cu lungimea (1/3) ⁿ . Pentru fiecare n∈N rezultă f _n (0) = 0, f _n (1) = 1. În figura f ₀ , se desenează f ₁ și f ₂ .

N + 1-a poligonală f _{n + 1} poate fi „construită” ca o transformare a lui f _n : de fapt, numită I _k ⁽ⁿ⁾ , k = 1, ..., 2 ⁿ și J _k ⁽ⁿ⁾ , k = 1, ..., 2 ⁿ -1 proiecțiile pe axa abscisei laturilor oblice și respectiv orizontale (rețineți că este f (J _k ⁽ⁿ⁾ ) = {k / 2 ⁿ }), atunci este f _{n + 1} = f _n în J _k ⁽ⁿ⁾ pentru fiecare k, în timp ce fiecare parte oblică a lui f _n (care are intervalul I _k ⁽ⁿ⁾ ca proiecție pe axa abscisei) este modificată în trei laturi, dintre care două sunt oblici în corespondență la intervalele I _2k-1 ^{(n + 1)} și I _2k ^{(n + 1)} , și unul orizontal la intervalul J _2k-1 ^{(n + 1)} .

Se poate dovedi că rezultă:

\sup _{p\in \mathbb {N} \ }{\big \{}\max _{x\in [0,1]}\{f_{n}(x)-f_{n+p}(x)\}{\big \}}\leq \ {\frac {1}{3\cdot 2^{n}}}

{\ displaystyle \ sup _ {p \ in \ mathbb {N} \} {\ big \ {} \ max _ {x \ in [0,1]} \ {f_ {n} (x) -f_ {n + p} (x) \} {\ big \}} \ leq \ {\ frac {1} {3 \ cdot 2 ^ {n}}}}

\ sup _ {{p \ in {\ mathbb {N}} \}} {\ big \ {} \ max _ {{x \ in [0,1]}} \ {f _ {{n}} (x ) -f _ {{n + p}} (x) \} {\ big \}} \ leq \ {\ frac {1} {3 \ cdot 2 ^ {{n}}}}

.

Din acest ultim rezultat rezultă că această succesiune este a lui Cauchy în spațiul funcțiilor continue din [0,1] . Prin urmare, pentru n → ∞ converge uniform către o funcție limită, care se numește funcție Cantor .

Proprietate

Funcția Cantor este o funcție continuă (ca limită uniformă a funcțiilor continue), crescătoare și surjectivă din intervalul [0, 1] în sine. Este de variație limitată, dar nu absolut continuă . Nu este diferențiat în niciun punct al setului Cantor , în timp ce în celelalte puncte este diferențiat și are zero derivate. Prin urmare, este o funcție constantă în fiecare subinterval de [0, 1] care nu conține puncte ale setului Cantor (ultimul set are măsură zero ), adică în intervale de tip (0. x ₁ x ₂ x ₃ ... x _n 022222 ..., 0. x ₁ x ₂ x ₃ ... x _n 200000 ...). În ciuda acestui fapt, este în creștere (în sens larg).

Funcția Cantor, limitată la setul Cantor, este întotdeauna continuă, crescând și surjectivă pe intervalul [0, 1]: aceasta implică faptul că setul Cantor nu poate fi numărat . Această funcție este utilă pentru definirea unei curbe Peano , adică o curbă care umple complet un pătrat.

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere bazate pe Cantor

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

V · D · M Teoria haosului
Teoria bifurcației	Furcă de bifurcație · Nod de șa de bifurcație · Bifurcație imperfectă · Bifurcație transcritică · Bifurcație Hopf · Larva Pin (sistem dinamic)
Fractale	Arta fractală · Buddhabrot · navă de ardere · compresie fractală · Koch fulg de zăpadă · curba Peano · curba Sierpinski · Dimensiunea Hausdorff · dimensiunii fractale · Funcția Cantor · Set Cantor · Set Julia · Mandelbrot · Fractalii pentru dimensiune Hausdorff · Cantor de praf · Sterling · Sierpinski Triangle · Dimensiunea Minkowski-Bouligand
Atractorii	Sistem Lorenz · Atractorul din Hénon · Harta Poincaré · Harta logistică · Harta potcoavelor · Spațiul de fază
Teoreticienii haosului	Edward Norton Lorenz · Aleksandr Lyapunov · Benoît Mandelbrot · Edward October · Henri Poincare · David Ruelle · Stephen Wolfram · James Yorke