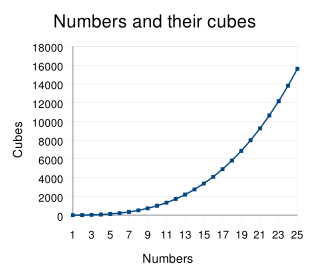
Cub perfect

Un cub perfect este orice număr natural a cărui rădăcină cubă corespunde unui număr întreg .

y = x³, pentru valori întregi 1≤x≤25.

În aritmetică și algebră , cubul unui număr n este a treia sa putere , adică rezultatul înmulțirii numărului cu el însuși de trei ori:

n ³ = n × n × n .

Este, de asemenea, formula pentru calcularea volumului unui cub a cărui latură are o lungime egală cu n . De aici și numele.

Funcția inversă de a găsi numărul al cărui cub este n se numește „extragerea rădăcinii cubice a lui n ”. Returnează partea laterală a unui cub având în vedere volumul.

Primii 21 de cuburi perfecte

0 = 0 ridicat la cub
1 = 1 ridicat la cub .
8 = 2 ridicat la cub .
27 = 3 ridicat la cub .
64 = 4 ridicat la cub .
125 = 5 ridicat la cub .
216 = 6 ridicat la cub .
343 = 7 ridicat la cub .
512 = 8 cub .
729 = 9 ridicat la cub .
1000 = 10 ridicat la cub .
1331 = 11 ridicat la cub .
1728 = 12 ridicate la cub .
2197 = 13 ridicat la cub .
2744 = 14 ridicat la cub .
3375 = 15 cub .
4096 = 16 ridicat la cub .
4913 = 17 ridicat la cub .
5832 = 18 ridicat la cub .
6859 = 19 ridicat la cub .
8000 = 20 cub .

Diferența dintre cuburile a două numere întregi consecutive poate fi exprimată ca:

n^{3}-(n-1)^{3}=3(n-1)n+1

{\ displaystyle n ^ {3} - (n-1) ^ {3} = 3 (n-1) n + 1}

{\ displaystyle n ^ {3} - (n-1) ^ {3} = 3 (n-1) n + 1}

sau

(n+1)^{3}-n^{3}=3(n+1)n+1

{\ displaystyle (n + 1) ^ {3} -n ^ {3} = 3 (n + 1) n + 1}

{\ displaystyle (n + 1) ^ {3} -n ^ {3} = 3 (n + 1) n + 1}

Aplicații

Cubul unui număr apare în formula de calcul al volumului unei sfere regulate, octaedru, dodecaedru, icosaedru, în suma pătratelor primelor n numere naturale , în a treia lege a lui Kepler .

Dacă kd ^ 2 se adaugă la produsul a trei termeni consecutivi ai unei progresii aritmetice cu primul termen a și motivul d ( a și d numere întregi pozitive), obținem un număr cub perfect K.
Produsul a trei termeni consecutivi ai unei progresii geometrice este un cub perfect.

Problema lui Waring pentru cuburi

Același subiect în detaliu: problema lui Waring .

Fiecare cub perfect poate fi scris ca suma a nouă sau mai puține cuburi pozitive. De exemplu, 23 nu poate fi scris ca suma a cel puțin nouă cuburi pozitive:

23 = 2 ³ + 2 ³ + 1 ³ + 1 ³ + 1 ³ + 1 ³ + 1 ³ + 1 ³ + 1 ³ .

Ultima teoremă a lui Fermat pentru cuburi

Același subiect în detaliu: Ultima teoremă a lui Fermat .

Ecuația $x^{3}+y^{3}=z^{3}$ ${\ displaystyle x ^ {3} + y ^ {3} = z ^ {3}}$ ${\ displaystyle x ^ {3} + y ^ {3} = z ^ {3}}$ nu are soluții întregi non-banale (de ex. xyz = 0). De fapt, nu are numere întregi Eisenstein ^[1]

ambele afirmații sunt valabile și pentru ecuația ^[2] $x^{3}+y^{3}=3z^{3}$ ${\ displaystyle x ^ {3} + y ^ {3} = 3z ^ {3}}$ ${\ displaystyle x ^ {3} + y ^ {3} = 3z ^ {3}}$ .

Acest lucru nu este adevărat dacă luăm în considerare suma cuburilor, cu mai mult de două completări:

3^{3}+4^{3}+5^{3}=6^{3}\,

{\ displaystyle 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 6 ^ {3} \,}

{\ displaystyle 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 6 ^ {3} \,}

Același subiect în detaliu: Cuaternul lui Ramanujan .

Suma primelor n cuburi

Cuburile numerelor naturale sunt suma blocurilor numerelor naturale impare în ordine crescătoare, exemplu:

\underbrace {1} _{1}\ \underbrace {3\ 5} _{8}\ \underbrace {7\ 9\ 11} _{27}\ \underbrace {13\ 15\ 17\ 19} _{64}\ \underbrace {21\ 23\ 25\ 27\ 29} _{125}\ \ldots

{\ displaystyle \ underbrace {1} _ {1} \ \ underbrace {3 \ 5} _ {8} \ \ underbrace {7 \ 9 \ 11} _ {27} \ \ underbrace {13 \ 15 \ 17 \ 19} _ {64} \ \ underbrace {21 \ 23 \ 25 \ 27 \ 29} _ {125} \ \ ldots}

{\ displaystyle \ underbrace {1} _ {1} \ \ underbrace {3 \ 5} _ {8} \ \ underbrace {7 \ 9 \ 11} _ {27} \ \ underbrace {13 \ 15 \ 17 \ 19} _ {64} \ \ underbrace {21 \ 23 \ 25 \ 27 \ 29} _ {125} \ \ ldots}

Începând cu succesiunea numerelor hexagonale centrate
${\begin{aligned}1&=1\\8&=1+7\\27&=1+7+19\\64&=1+7+19+37\\125&=1+7+19+37+61\\\ldots &=\ldots \end{aligned}}$ ${\ displaystyle {\ begin {align} 1 & = 1 \\ 8 & = 1 + 7 \\ 27 & = 1 + 7 + 19 \\ 64 & = 1 + 7 + 19 + 37 \\ 125 & = 1 + 7 + 19 + 37 +61 \\\ ldots & = \ ldots \ end {align}}}$ ${\ displaystyle {\ begin {align} 1 & = 1 \\ 8 & = 1 + 7 \\ 27 & = 1 + 7 + 19 \\ 64 & = 1 + 7 + 19 + 37 \\ 125 & = 1 + 7 + 19 + 37 +61 \\\ ldots & = \ ldots \ end {align}}}$

suma primelor n cuburi este al n-lea număr triunghiular pătrat

$1^{3}+2^{3}+\dots +n^{3}=(1+2+\dots +n)^{2}=\left({\frac {n(n+1)}{2}}\right)^{2}.$ ${\ displaystyle 1 ^ {3} + 2 ^ {3} + \ dots + n ^ {3} = (1 + 2 + \ dots + n) ^ {2} = \ left ({\ frac {n (n + 1)} {2}} \ right) ^ {2}.}$ ${\ displaystyle 1 ^ {3} + 2 ^ {3} + \ dots + n ^ {3} = (1 + 2 + \ dots + n) ^ {2} = \ left ({\ frac {n (n + 1)} {2}} \ right) ^ {2}.}$

Dovadă vizuală că 1 Șablon: Sup + 2 Șablon: Sup + 3 Șablon: Sup + 4 Șablon: Sup + 5 Șablon: Sup = (1 + 2 + 3 + 4 + 5) Șablon: Sup .

De exemplu, suma primelor 5 cuburi perfecte este pătratul celui de-al cincilea număr triunghiular

1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=15^{2}\,

{\ displaystyle 1 ^ {3} + 2 ^ {3} + 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 15 ^ {2} \,}

{\ displaystyle 1 ^ {3} + 2 ^ {3} + 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 15 ^ {2} \,}

dar x, y trebuie să satisfacă ecuația Pell negativă $x^{2}-2y^{2}=-1$ ${\ displaystyle x ^ {2} -2y ^ {2} = - 1}$ ${\ displaystyle x ^ {2} -2y ^ {2} = - 1}$ . De exemplu pentru y = 5 și 29, atunci,

1^{3}+3^{3}+\dots +9^{3}=(7\cdot 5)^{2}\,

{\ displaystyle 1 ^ {3} + 3 ^ {3} + \ dots + 9 ^ {3} = (7 \ cdot 5) ^ {2} \,}

{\ displaystyle 1 ^ {3} + 3 ^ {3} + \ dots + 9 ^ {3} = (7 \ cdot 5) ^ {2} \,}

1^{3}+3^{3}+\dots +57^{3}=(41\cdot 29)^{2}

{\ displaystyle 1 ^ {3} + 3 ^ {3} + \ dots + 57 ^ {3} = (41 \ cdot 29) ^ {2}}

{\ displaystyle 1 ^ {3} + 3 ^ {3} + \ dots + 57 ^ {3} = (41 \ cdot 29) ^ {2}}

si asa mai departe. Fiecare număr perfect , cu excepția minorului, este suma primilor $2^{(}(p-1)/2)$ ${\ displaystyle 2 ^ {(} (p-1) / 2)}$ ${\ displaystyle 2 ^ {(} (p-1) / 2)}$ cuburi impare:

28=2^{2}(2^{3}-1)=1^{3}+3^{3}

{\ displaystyle 28 = 2 ^ {2} (2 ^ {3} -1) = 1 ^ {3} + 3 ^ {3}}

{\ displaystyle 28 = 2 ^ {2} (2 ^ {3} -1) = 1 ^ {3} + 3 ^ {3}}

496=2^{4}(2^{5}-1)=1^{3}+3^{3}+5^{3}+7^{3}

{\ displaystyle 496 = 2 ^ {4} (2 ^ {5} -1) = 1 ^ {3} + 3 ^ {3} + 5 ^ {3} + 7 ^ {3}}

{\ displaystyle 496 = 2 ^ {4} (2 ^ {5} -1) = 1 ^ {3} + 3 ^ {3} + 5 ^ {3} + 7 ^ {3}}

8128=2^{6}(2^{7}-1)=1^{3}+3^{3}+5^{3}+7^{3}+9^{3}+11^{3}+13^{3}+15^{3}

{\ displaystyle 8128 = 2 ^ {6} (2 ^ {7} -1) = 1 ^ {3} + 3 ^ {3} + 5 ^ {3} + 7 ^ {3} + 9 ^ {3} + 11 ^ {3} + 13 ^ {3} + 15 ^ {3}}

{\ displaystyle 8128 = 2 ^ {6} (2 ^ {7} -1) = 1 ^ {3} + 3 ^ {3} + 5 ^ {3} + 7 ^ {3} + 9 ^ {3} + 11 ^ {3} + 13 ^ {3} + 15 ^ {3}}

Suma de cuburi de numere în progresie aritmetică

Există exemple de cuburi de numere în progresie aritmetică a căror sumă este un cub:

3^{3}+4^{3}+5^{3}=6^{3}

{\ displaystyle 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 6 ^ {3}}

{\ displaystyle 3 ^ {3} + 4 ^ {3} + 5 ^ {3} = 6 ^ {3}}

11^{3}+12^{3}+13^{3}+14^{3}=20^{3}

{\ displaystyle 11 ^ {3} + 12 ^ {3} + 13 ^ {3} + 14 ^ {3} = 20 ^ {3}}

{\ displaystyle 11 ^ {3} + 12 ^ {3} + 13 ^ {3} + 14 ^ {3} = 20 ^ {3}}

31^{3}+33^{3}+35^{3}+37^{3}+39^{3}+41^{3}=66^{3}

{\ displaystyle 31 ^ {3} + 33 ^ {3} + 35 ^ {3} + 37 ^ {3} + 39 ^ {3} + 41 ^ {3} = 66 ^ {3}}

{\ displaystyle 31 ^ {3} + 33 ^ {3} + 35 ^ {3} + 37 ^ {3} + 39 ^ {3} + 41 ^ {3} = 66 ^ {3}}

Formula F pentru a găsi suma de n cuburi de numere în progresie aritmetică, având diferența comună d începând de la un cub inițial $a^{3}$ ${\ displaystyle a ^ {3}}$ $a ^ {3}$ , Și:

F(d,a,n)=a^{3}+(a+d)^{3}+(a+2d)^{3}+\cdots +(a+dn-d)^{3}

{\ displaystyle F (d, a, n) = a ^ {3} + (a + d) ^ {3} + (a + 2d) ^ {3} + \ cdots + (a + dn-d) ^ { 3}}

{\ displaystyle F (d, a, n) = a ^ {3} + (a + d) ^ {3} + (a + 2d) ^ {3} + \ cdots + (a + dn-d) ^ { 3}}

este dat de

F(d,a,n)=(n/4)(2a-d+dn)(2a^{2}-2ad+2adn-d^{2}n+d^{2}n^{2})

{\ displaystyle F (d, a, n) = (n / 4) (2a-d + dn) (2a ^ {2} -2ad + 2adn-d ^ {2} n + d ^ {2} n ^ { 2})}

{\ displaystyle F (d, a, n) = (n / 4) (2a-d + dn) (2a ^ {2} -2ad + 2adn-d ^ {2} n + d ^ {2} n ^ { 2})}

O soluție parametrică

F(d,a,n)=y^{3}

{\ displaystyle F (d, a, n) = y ^ {3}}

{\ displaystyle F (d, a, n) = y ^ {3}}

e cunoscut pentru $d=1$ ${\ displaystyle d = 1}$ ${\ displaystyle d = 1}$ , sau cuburi consecutive, dar soluțiile non-sporadice sunt cunoscute și pentru numere întregi $d>1$ ${\ displaystyle d> 1}$ ${\ displaystyle d> 1}$ , Care $2,3,5,7,11,13,37,39,etc.$ ${\ displaystyle 2,3,5,7,11,13,37,39 etc.}$ ${\ displaystyle 2,3,5,7,11,13,37,39 etc.}$ ^[3]

Suma reciprocelor

Suma reciprocelor tuturor cuburilor, folosită într-o varietate de situații, este cunoscută sub numele de constanta Apéry . Valoarea sa este dată de funcția zeta Riemann la punctul 3.

\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}=\zeta {(3)}=1{,}2020569\ldots

{\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {3}}} = \ zeta {(3)} = 1 {,} 2020569 \ ldots}

{\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {3}}} = \ zeta {(3)} = 1 {,} 2020569 \ ldots}

În număr rațional

Fiecare număr rațional pozitiv este suma a trei cuburi raționale pozitive ^[4] , în timp ce există raționale care nu sunt suma a două cuburi raționale. ^[5]

Funcție generatoare

Funcția generatoare $\sum _{i\geq 0}a_{i}x^{i}$ ${\ displaystyle \ sum _ {i \ geq 0} a_ {i} x ^ {i}}$ ${\ displaystyle \ sum _ {i \ geq 0} a_ {i} x ^ {i}}$ a unei serii formale de puteri $(a_{i})_{i\geq 0}$ ${\ displaystyle (a_ {i}) _ {i \ geq 0}}$ ${\ displaystyle (a_ {i}) _ {i \ geq 0}}$ , este dat de:

\sum _{i\geq 0}i^{3}x^{i}=x+8x^{2}+27x^{3}+64x^{4}+\ldots ={\frac {x(x^{2}+4x+1)}{(x-1)^{4}}}

{\ displaystyle \ sum _ {i \ geq 0} i ^ {3} x ^ {i} = x + 8x ^ {2} + 27x ^ {3} + 64x ^ {4} + \ ldots = {\ frac { x (x ^ {2} + 4x + 1)} {(x-1) ^ {4}}}}

{\ displaystyle \ sum _ {i \ geq 0} i ^ {3} x ^ {i} = x + 8x ^ {2} + 27x ^ {3} + 64x ^ {4} + \ ldots = {\ frac { x (x ^ {2} + 4x + 1)} {(x-1) ^ {4}}}}

Istorie

Calculul cubului cu numere mari este comun în istoria matematicii .
În 2010, Alberto Zanoni a descoperit un algoritm ^[6] ^[7] pentru calcularea cubului unui întreg întreg, într-un anumit interval, mai rapid decât exponențierea binară (crescând la puteri întregi pozitive mari cu un număr).

Notă

^ Hardy & Wright, Thm. 227
^ Hardy & Wright, Thm. 232
^ O colecție de identități algebrice ^{[ link rupt ]} , pe sites.google.com .
^ Hardy & Wright, Thm. 234
^ Hardy & Wright, Thm. 233
^ http://bodrato.it/papers/zanoni/AnotherSugarCube.pdf
^ Un nou algoritm pentru calculul cubului întregului lung cu o oarecare perspectivă asupra puterilor superioare | SpringerLink

.

Bibliografie

Hardy GH, Wright EM, An Introduction to Theory of Numbers , ediția a 5-a, Oxford University Press , Oxford, 1980, ISBN 978-0-19-853171-5

Elemente conexe

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Hardy & Wright, Thm. 227

[2] Hardy & Wright, Thm. 232

[3] O colecție de identități algebrice ^{[ link rupt ]} , pe sites.google.com .

[4] Hardy & Wright, Thm. 234

[5] Hardy & Wright, Thm. 233

[6] ttp://bodrato.it/papers/zanoni/AnotherSugarCube.pdf

[7] Un nou algoritm pentru calculul cubului întregului lung cu o oarecare perspectivă asupra puterilor superioare | SpringerLink

[1]

[2]

[3]

[4]

[5]

[6]

[7]

V · D · M Numere figurate
Numere poligonale	Triunghiulara Număr · Număr pătrat · Număr pentagonală · Număr hexagonala · Număr heptagonala · Număr octogonal · Număr nonagonal · Număr decagonal · Număr de formă alungită · Număr poligonală centrală
Numere de poligon centrate	Număr triunghiular centrat · Număr centrat pătrat · pentagonal Număr centrat · hexagonal Număr centrat · heptagonal Număr centrat · octogonal Număr centrat · număr nonagonal centrat · Număr decagonal centrat · Număr stelat
Numere poliedrice	Tetraedral Numărul · Numărul piramidală pătrat · pentagonală piramidale număr · piramidă hexagonală Număr · piramidă Număr heptagonala · Număr octaedrala · Număr octaedrala trunchiate · stele Număr octangulare · Număr cilindrică · Nr cubică
Numere politopice	Număr de Pentatopic · Hypercubic numărul
Alte	Teorema lui Fermat asupra numerelor poligonale