vector Lenz

În mecanica clasică , Laplace - Runge - vectorul Lenz (sau pur și simplu , vectorul Lenz) este un vector utilizat în mod obișnuit pentru a descrie forma și orientarea orbita a unui corp ceresc în jurul altuia, ca și în cazul revoluției unei planete în jurul valorii de soare. Pentru două organisme în conformitate cu care interacționează gravitația newtoniană , vectorul Lenz este o constantă a mișcării , în sensul că, pentru o anumită orbită, își păstrează aspectul , indiferent de punctul sau din momentul în care aceasta se calculează în ^{[1 ]} ; într-un mod echivalent, vectorul poate fi spus să fie „conservat“ în timpul mișcării. Mai general, acest vector este stocat în toate problemele în care două corpuri interacționează prin intermediul unei forță centrală care variază în conformitate cu legea invers proporțional cu pătratul distanței; aceste probleme sunt dublate probleme Kepler ^[2] .

Atomul de hidrogen este un exemplu de o problemă de acest tip, deoarece acesta cuprinde două particule Interactiunea încărcat prin forța Coulomb . Vectorul de Lenz acoperit o funcție foarte importantă în prima derivarea cuantică a spectrului de emisie al atomului de hidrogen ^[3] , înainte de dezvoltarea " ecuației Schrödinger . Cu toate acestea, această abordare este greu folosit astăzi.

În mecanica clasică și cuantică, cantitățile conservate corespund , în general simetrii ale sistemului. Conservarea corespunde vectorului Lenz o simetrie oarecum neobișnuită: problema Kepler este de fapt matematic echivalent cu cel al unei mișcări libere de particule , la granița tridimensională a unui " hipersfere , ^[4] , astfel încât întreaga problemă este simetrică în ceea ce privește anumite rotații ale acestui spațiu cu patru dimensiuni ^[5] . Această simetrie ridicată este rezultatul a două proprietăți ale problemei Kepler: vectorul viteză se mișcă într - un cerc perfect și amenajat pentru energie mecanică, toate acestea se intersectează cercuri de viteză de-a lungul aceleași două puncte ^[6] .

Multe generalizări ale vectorului Lenz au fost dezvoltate cu scopul de a integra efectele relativității speciale , câmpuri electromagnetice sau alte tipuri de forțe centrale.

Context

O mișcare singură particulă într-un câmp central al forțelor conservatoare are cel mult patru constante ale mișcării: energia totală $ȘI$ ${\ displaystyle E}$ $ȘI$ iar cele trei componente carteziene ale momentului unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ . Orbita particulei este limitată la un plan definit de momentul Acasă $\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ ${\ mathbf p}$ (Sau, echivalent, cu viteză $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf v$ ) Și raza vectorului $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ între particula în sine și centrul câmpului de forță.

Așa cum sa definit anterior, vectorul Lenz $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ acesta se află întotdeauna în planul orbital al oricărei forțe centrale. Cu toate acestea, este constantă numai pentru o forță centrală care descrește conform legii pătratul ^[1] . Pentru cea mai mare parte a forțelor centrale, cu toate acestea, $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ nu este constantă, ci se schimbă atât în lungime și în direcție; în cazul în care forța de numai aproximativ Reacția produsă la criteriul de mai sus, vectorul $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ este destul de constantă în lungime, dar se rotește încet direcție. O formă mai generală a vectorului Lenz, notat prin ${\mathcal {A}}$ ${\ displaystyle {\ mathcal {A}}}$ ${\ mathcal {A}}$ , Dar acest nou vector se dovedește a fi o funcție destul de complicată a poziției, și în general nu poate fi exprimat într-o formă compactă. ^[7] ^[8]

Avionul pe care are loc mișcarea este perpendicular pe vectorul momentului unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ , Care este constantă; acest proprietăți geometrice pot fi exprimate matematic prin ecuația produsului scalar dintre vectorii $\mathbf {r} \cdot \mathbf {L} =0$ ${\ Displaystyle \ mathbf {r} \ cdot \ mathbf {L} = 0}$ ${\ Displaystyle \ mathbf {r} \ cdot \ mathbf {L} = 0}$ ; În mod similar, din moment ce $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ se află în același plan, $\mathbf {A} \cdot \mathbf {L} =0$ ${\ Displaystyle \ mathbf {A} \ cdot \ mathbf {L} = 0}$ ${\ Displaystyle \ mathbf {A} \ cdot \ mathbf {L} = 0}$ .

Istoria redescoperirea

vectorul lui Lenz $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ Este o constantă a mișcării în problema Kepler, și este utilă pentru a descrie orbitele corpurilor cerești, cum ar fi cazul mișcării unei planete în jurul Soarelui . Cu toate acestea, a fost pentru o lungă perioadă de timp puțin cunoscute și utilizate printre fizicieni, probabil pentru că este mai puțin intuitiv la alte cantități , cum ar fi timpul și momentul cinetic . Ca urmare, acesta a fost în mod independent „redescoperit“ de mai multe ori pe parcursul ultimelor trei secole. Jakob Hermann a fost primul care arata ca $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ este o constantă în cazul forțelor centrale , cu proporționalitate inversă pătratic ^[9] și realizat pe studii despre legătura sa cu excentricitatea orbitelor cerești. Munca lui a fost generalizată în forma sa modernă de Johann Bernoulli în 1710. ^[10] La sfârșitul secolului, Pierre-Simon de Laplace redescoperit conservarea $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ , Ea derivând analitic, mai degrabă decât geometrica. ^[11] În secolul mediu al nouăsprezecelea, William Rowan Hamilton a atras echivalent vectorul excentricitate și folosit pentru a arăta că vectorul timp $\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ ${\ mathbf p}$ se mișcă de-a lungul unui cerc prin mișcări în domenii ale forțelor centrale (Figura 3). La începutul secolului XX, Josiah Willard Gibbs derivat același vector utilizând metode de analiză vectorială . ^[12] Derivarea Gibbs a fost folosit pentru a mo „eșantion din Carle Runge într - o carte populară a textului german asupra transportatorilor, ^[13] , care a fost la rândul său , citat de Wilhelm Lenz în textul său pe (vechi) discuția în mecanica cuantică atom al spectrului de hidrogen . ^[14] În 1926, vectorul a fost utilizat de către Wolfgang Pauli pentru a obține spectrul hidrogenului folosind formularea de matrice a mecanicii cuantice, dar nu l ' ecuatia Schrodinger ; după publicarea Pauli lui, a devenit cunoscut sub numele de „vectorul Runge-Lenz“.

Definiție matematică

Pentru o singură particulă se deplasează într-un câmp de forță centrală descrisă de ecuația $\mathbf {F} (r)=-{\frac {k}{r^{2}}}\mathbf {\hat {r}}$ ${\ Displaystyle \ mathbf {F} (r) = - {\ frac {k} {r ^ {2}}} \ mathbf {\ hat {r}}}$ ${\ Displaystyle \ mathbf {F} (r) = - {\ frac {k} {r ^ {2}}} \ mathbf {\ hat {r}}}$ , Vectorul Lenz $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ Acesta este definit de formula ^[1]

Figura 1: Vectorul Lenz

\mathbf {A}

{\ displaystyle \ mathbf {A}}

\ mathbf A

(În roșu), la patru puncte (indicate 1, 2, 3 și 4) pe orbita eliptică a unui punct material se deplasează într-un câmp de forțe centrale. Centrul de atracție este indicat printr-un cerc mic negru din care vectorul de poziție (negru) provine. Purtătorul impuls unghiular

\mathbf {L}

{\ displaystyle \ mathbf {L}}

{\ mathbf L}

este perpendicular pe orbita. vectori coplanari

\mathbf {p} \times \mathbf {L}

{\ Displaystyle \ mathbf {p} \ ori \ mathbf {L}}

{\ Displaystyle \ mathbf {p} \ ori \ mathbf {L}}

Și

{\frac {mk}{r}}\mathbf {r}

{\ Displaystyle {\ frac {mk} {r}} \ mathbf {r}}

{\ Displaystyle {\ frac {mk} {r}} \ mathbf {r}}

acestea sunt în albastru și verde, respectiv. Vectorul

\mathbf {A}

{\ displaystyle \ mathbf {A}}

\ mathbf A

este constantă în direcția și modulul.

\mathbf {A} =\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} =m^{2}\mathbf {v} \times \mathbf {l} -mk\mathbf {\hat {r}}

{\ Displaystyle \ mathbf {A} = \ mathbf {p} \ ori \ mathbf {L} -MK \ mathbf {\ hat {r}} = m ^ {2} \ mathbf {v} \ ori \ mathbf {l} -MK \ mathbf {\ hat {r}}}

{\ Displaystyle \ mathbf {A} = \ mathbf {p} \ ori \ mathbf {L} -MK \ mathbf {\ hat {r}} = m ^ {2} \ mathbf {v} \ ori \ mathbf {l} -MK \ mathbf {\ hat {r}}}

unde este

$m$ ${\ displaystyle m}$ $m$ este masa a punctului material,
$\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ $\ mathbf {p}$ Acesta este vectorul impuls și $\mathbf {v}$ ${\ displaystyle \ mathbf {v}}$ $\ mathbf {v}$ viteza,
$\mathbf {L} =\mathbf {r} \times \mathbf {p}$ ${\ displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p}}$ ${\ displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p}}$ este vectorul momentului cinetic și $\mathbf {l}$ ${\ Displaystyle \ mathbf {l}}$ ${\ Displaystyle \ mathbf {l}}$ taxa specifică pe unitate de masă,
$k$ ${\ displaystyle k}$ $k$ Acesta este parametrul care descrie intensitatea forței centrale (echivalent cu $GMm=\mu m$ ${\ Displaystyle GMM = \ mu m}$ ${\ Displaystyle GMM = \ mu m}$ în cazul EA gravitaționale $k^{*}Qq$ ${\ K displaystyle ^ {*}} Qq$ ${\ K displaystyle ^ {*}} Qq$ în cel electrostatic),
$\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ este vectorul de poziție al particulei (Figura 1), și
$\mathbf {\hat {r}}$ ${\ displaystyle \ mathbf {\ hat {r}}}$ ${\ displaystyle \ mathbf {\ hat {r}}}$ este corespunzător versorul , $\mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}$ ${\ Displaystyle \ mathbf {\ hat {r}} = {\ frac {\ mathbf {r}} {r}}}$ ${\ Displaystyle \ mathbf {\ hat {r}} = {\ frac {\ mathbf {r}} {r}}}$ unde este $r$ ${\ displaystyle r}$ $r$ este forma $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ .

Deoarece forța este considerată conservatoare, energia totală $ȘI$ ${\ displaystyle E}$ $ȘI$ este o constantă de mișcare

E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}

{\ Displaystyle E = {\ frac {p ^ {2}} {2m}} - {\ frac {k} {r}} = {\ frac {1} {2}} mv ^ {2} - {\ frac {k} {r}}}

{\ Displaystyle E = {\ frac {p ^ {2}} {2m}} - {\ frac {k} {r}} = {\ frac {1} {2}} mv ^ {2} - {\ frac {k} {r}}}

.

Mai mult, este de asemenea, o forță centrală și, prin urmare, vectorul momentului unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ este, de asemenea conservat și definește planul în care se mișcă de particule. vectorul lui Lenz $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ Este perpendicular pe momentul cinetic $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ de cand este $\mathbf {p} \times \mathbf {L}$ ${\ Displaystyle \ mathbf {p} \ ori \ mathbf {L}}$ ${\ Displaystyle \ mathbf {p} \ ori \ mathbf {L}}$ acea $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ sunt perpendiculare $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ . Din aceasta rezultă că $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ se află în planul orbitei.

Această definiție a vectorului Lenz se referă la un singur punct material de masă $m$ ${\ displaystyle m}$ $m$ în mișcare sub acțiunea unei forțe fixe. Cu toate acestea, aceeași definiție poate fi extinsă la cazul celor două corpuri ca problema Kepler pozand $m$ ${\ displaystyle m}$ $m$ egal cu masa redusă a celor două corpuri și $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ ca raza vectorului între cele două corpuri.

Multe variante ale vectorului Lenz poate fi folosit pentru a exprima aceeași constantă de mișcare. Cel mai utilizat este vectorul excentricitatea, obținut din $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ după o divizie de $m k$ ${\ Displaystyle mk}$ ${\ Displaystyle mk}$ .

\mathbf {e} ={\frac {\mathbf {A} }{mk}}={\frac {1}{mk}}(\mathbf {p} \times \mathbf {L} )-\mathbf {\hat {r}}

{\ Displaystyle \ mathbf {e} = {\ frac {\ mathbf {A}} {mk}} = {\ frac {1} {mk}} (\ mathbf {p} \ ori \ mathbf {L}) - \ mathbf {\ hat {r}}}

{\ Displaystyle \ mathbf {e} = {\ frac {\ mathbf {A}} {mk}} = {\ frac {1} {mk}} (\ mathbf {p} \ ori \ mathbf {L}) - \ mathbf {\ hat {r}}}

.

Derivarea geometriei orbitale

Figura 2: versiune simplificată din figura 1, cu unghiul reprezentat

\theta

{\ displaystyle \ theta}

\ theta

între

\mathbf {A}

{\ displaystyle \ mathbf {A}}

\ mathbf A

și

\mathbf {r}

{\ displaystyle \ mathbf {r}}

\ mathbf r

într-un punct al orbitei.

Forma și orientarea orbitei poate fi determinată din vectorul Lenz după cum urmează. ^[1] Prin realizarea produsului scalar între $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ și poziția vectorului $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ obținem ecuația:

\mathbf {A} \cdot \mathbf {r} =Ar\cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)-mkr

{\ Displaystyle \ mathbf {A} \ cdot \ mathbf {r} = Ar \ cos \ theta = \ mathbf {r} \ cdot \ stânga (\ mathbf {p} \ ori \ mathbf {L} \ dreapta) -mkr}

{\ Displaystyle \ mathbf {A} \ cdot \ mathbf {r} = Ar \ cos \ theta = \ mathbf {r} \ cdot \ stânga (\ mathbf {p} \ ori \ mathbf {L} \ dreapta) -mkr}

unde este $\theta$ ${\ displaystyle \ theta}$ $\ theta$ este unghiul dintre $\mathbf {r}$ ${\ displaystyle \ mathbf {r}}$ $\ mathbf r$ și $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ (Figura 2). Prin permutare produsul triplu dot

\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)=\left(\mathbf {r} \times \mathbf {p} \right)\cdot \mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}

{\ Displaystyle \ mathbf {r} \ cdot \ stânga (\ mathbf {p} \ ori \ mathbf {L} \ dreapta) = \ stânga (\ mathbf {r} \ ori \ mathbf {p} \ dreapta) \ cdot \ mathbf {L} = \ mathbf {L} \ cdot \ mathbf {L} = L ^ {2}}

{\ Displaystyle \ mathbf {r} \ cdot \ stânga (\ mathbf {p} \ ori \ mathbf {L} \ dreapta) = \ stânga (\ mathbf {r} \ ori \ mathbf {p} \ dreapta) \ cdot \ mathbf {L} = \ mathbf {L} \ cdot \ mathbf {L} = L ^ {2}}

și rearanjarea formula este obținut, valabil pentru secțiunile conice

{\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)

{\ Displaystyle {\ frac {1} {r}} = {\ frac {mk} {L ^ {2}}} \ stânga (1 + {\ frac {A} {mk}} \ cos \ theta \ dreapta) }

{\ Displaystyle {\ frac {1} {r}} = {\ frac {mk} {L ^ {2}}} \ stânga (1 + {\ frac {A} {mk}} \ cos \ theta \ dreapta) }

excentricitate $Și$ ${\ displaystyle e}$ $Și$

e={\frac {A}{mk}}={\frac {\left|\mathbf {A} \right|}{mk}}

{\ Displaystyle e = {\ frac {A} {mk}} = {\ frac {\

din

stânga | \ mathbf {A} \ dreapta |} {mk}}}

{\ Displaystyle e = {\ frac {A} {mk}} = {\ frac {\ din stânga | \ mathbf {A} \ dreapta |} {mk}}}

și partea dreaptă

\left|4p\right|={\frac {2L^{2}}{mk}}

{\ Displaystyle \ left | 4P \ dreapta | = {\ frac {2L ^ {2}} {mk}}}

{\ Displaystyle \ left | 4P \ dreapta | = {\ frac {2L ^ {2}} {mk}}}

Axa semi-majoră $la$ ${\ displaystyle a}$ $la$ din secțiunea conică poate fi definit pornind de pe partea dreaptă și de excentricitatea

a\left(1\pm e^{2}\right)=2p={\frac {L^{2}}{mk}}

{\ Displaystyle un \ stânga (1 \ pm e ^ {2} \ dreapta) = 2p = {\ frac {L ^ {2}} {mk}}}

{\ Displaystyle un \ stânga (1 \ pm e ^ {2} \ dreapta) = 2p = {\ frac {L ^ {2}} {mk}}}

în cazul în care semnul minus este doar de „ elipsă , și de cele mai multe“ semn hiperbolă .

Produsul punct de $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ cu ea însăși dă naștere la o ecuație care conține energie mecanică $ȘI$ ${\ displaystyle E}$ $ȘI$ :

A^{2}=m^{2}k^{2}+2mEL^{2}\,

{\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2} \,}

{\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2} \,}

care pot fi scrise în termeni de excentricitate:

e^{2}-1={\frac {2L^{2}}{mk^{2}}}E

{\ Displaystyle e ^ {2} -1 = {\ frac {2L ^ {2}} {mk ^ {2}}} E}

{\ Displaystyle e ^ {2} -1 = {\ frac {2L ^ {2}} {mk ^ {2}}} E}

.

Deci, în cazul în care energia $ȘI$ ${\ displaystyle E}$ $ȘI$ este negativ (orbita închis), excentricitatea este mai mică decât una și orbita este o " elipsă . Pe de altă parte , în cazul în care energia este pozitivă (orbita deschisă), excentricitatea este mai mare decât una și orbita este reprezentat de un " hiperbolă . În cele din urmă, în cazul în care energia este exact zero, excentricitatea este una, iar orbita are o formă parabolică. În toate cazurile luate în considerare, gestionarea $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ se afla de-a lungul axei de simetrie a secțiunii conice și puncte din centrul forței spre absida, punctul de proximitate maxim.

Odograph circulară a momentului

Figura 3: Vectorul momentul

\mathbf {p}

{\ displaystyle \ mathbf {p}}

{\ mathbf p}

(În albastru) se mișcă pe un cerc, în timp ce se deplasează de-a lungul unei elipse de particule. Cele patru puncte subliniate corespund celor din figura 1. cercul este centrat pe axa

y

{\ displaystyle y}

y

la loc

{\frac {A}{L}}

{\ Displaystyle {\ frac {A} {L}}}

{\ Displaystyle {\ frac {A} {L}}}

(În magenta), cu raza

{\frac {mk}{L}}

{\ Displaystyle {\ frac {mk} {L}}}

{\ Displaystyle {\ frac {mk} {L}}}

(verde). Coltul

\eta

{\ displaystyle \ eta}

\vârstă

determină excentricitatea

Și

{\ displaystyle e}

Și

orbitei eliptice

(\cos \eta =e)

{\ Displaystyle (\ cos \ vârstă = e)}

{\ Displaystyle (\ cos \ vârstă = e)}

.

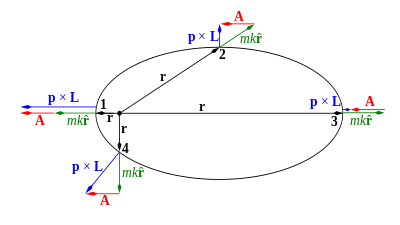
Conservarea vectorului Lenz $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ și vectorul momentului unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ este foarte util pentru a arăta că vectorul momentul (impuls) $\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ ${\ mathbf p}$ Se mișcă pe un cerc , în cazul unei forțe centrale. ^[6]

Prin rularea produsul scalar al

mk~{\hat {\mathbf {r} }}=\mathbf {p} \times \mathbf {L} -\mathbf {A}

{\ Displaystyle mk ~ {\ hat {\ mathbf {r}}} = \ mathbf {p} \ ori \ mathbf {L} - \ mathbf {A}}

{\ Displaystyle mk ~ {\ hat {\ mathbf {r}}} = \ mathbf {p} \ ori \ mathbf {L} - \ mathbf {A}}

cu ea însăși obținem:

(mk)^{2}=A^{2}+p^{2}L^{2}+2\mathbf {L} \cdot (\mathbf {p} \times \mathbf {A} )~.

{\ Displaystyle (mk) ^ {2} = A ^ {2} + p ^ {2} L ^ {2} 2 \ mathbf {L} \ cdot (\ mathbf {p} \ ori \ mathbf {A}) ~.}

{\ Displaystyle (mk) ^ {2} = A ^ {2} + p ^ {2} L ^ {2} 2 \ mathbf {L} \ cdot (\ mathbf {p} \ ori \ mathbf {A}) ~.}

Mai târziu, alegerea $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ de-a lungul axei $z$ ${\ displaystyle z}$ $z$ Și semi-majoră axa ca axă $X$ ${\ displaystyle x}$ $X$ , Obținem ecuația pentru $\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ ${\ mathbf p}$

p_{x}^{2}+\left(p_{y}-A/L\right)^{2}=\left(mk/L\right)^{2}~.

{\ Displaystyle P_ {x} ^ {2} + \ stânga (P_ {y} -A / L \ dreapta) ^ {2} = \ stânga (mk / L \ dreapta) ^ {2} ~.}

{\ Displaystyle P_ {x} ^ {2} + \ stânga (P_ {y} -A / L \ dreapta) ^ {2} = \ stânga (mk / L \ dreapta) ^ {2} ~.}

.

Cu alte cuvinte, vectorul impuls $\mathbf {p}$ ${\ displaystyle \ mathbf {p}}$ ${\ mathbf p}$ este limitată la un cerc de rază ${\frac {mk}{L}}$ ${\ Displaystyle {\ frac {mk} {L}}}$ ${\ Displaystyle {\ frac {mk} {L}}}$ centrat în punct $\left(0,{\frac {A}{L}}\right)$ ${\ Displaystyle \ stânga (0, {\ frac {A} {L}} \ dreapta)}$ ${\ Displaystyle \ stânga (0, {\ frac {A} {L}} \ dreapta)}$ . excentricitatea $Și$ ${\ displaystyle e}$ $Și$ corespunde cosinusul unghiului $\eta$ ${\ displaystyle \ eta}$ $\vârstă$ prezentat în figura 3. în limita orbitei circulare și, prin urmare, la anularea $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ , Cercul are centrul în originea $(0;0)$ ${\ displaystyle (0; 0)}$ ${\ displaystyle (0; 0)}$ . Din motive de concizie, este de asemenea util să se introducă variabila $p_{0}={\sqrt {2m\left|E\right|}}$ ${\ Displaystyle P_ {0} = {\ sqrt {2m \$ din $stânga | E \ dreapta |}}}$ ${\ Displaystyle P_ {0} = {\ sqrt {2m \ din stânga | E \ dreapta |}}}$ . Acest odograph circular este util pentru ilustrarea simetria problemei Kepler.

Constantele de mișcare și superintegrability

Cele șapte cantități scalare $ȘI$ ${\ displaystyle E}$ $ȘI$ , $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ și $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ (Fiind vectori, ultimele două contribuie trei cantități fiecare) sunt legate de două ecuații, $\mathbf {A} \cdot \mathbf {L} =0$ ${\ Displaystyle \ mathbf {A} \ cdot \ mathbf {L} = 0}$ ${\ Displaystyle \ mathbf {A} \ cdot \ mathbf {L} = 0}$ Și $A^{2}=m^{2}k^{2}+2mEL^{2}$ ${\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2}}$ ${\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2}}$ , Dând naștere la cinci constante ale mișcării independente. Acest rezultat este în concordanță cu cele șase condiții inițiale (adică, viteza și poziția vectorilor particulei, a trei componente fiecare) care specifica orbita corpului, deoarece momentul de pornire nu este determinată de aceste constante. Deoarece forma $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ (Si excentricitatea orbitala aferente $Și$ ${\ displaystyle e}$ $Și$ ) Poate fi determinată din momentul cinetic $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ și energie $ȘI$ ${\ displaystyle E}$ $ȘI$ , Numai direcția $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ este păstrat în mod independent; în plus, deoarece $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ trebuie să fie întotdeauna perpendicular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ , Contribuie doar cu o cantitate suplimentară stocată.

Un sistem mecanic cu $d$ ${\ displaystyle d}$ $d$ grade de libertate poate avea cel mult $2d-1$ ${\ Displaystyle 2d-1}$ ${\ Displaystyle 2d-1}$ Constantele de mișcare , deoarece există $2d$ ${\ displaystyle 2d}$ ${\ displaystyle 2d}$ condițiile inițiale și momentul inițial nu poate fi determinată de o constantă. Un sistem cu mai mult $d$ ${\ displaystyle d}$ $d$ Constantele de mișcare se numește superintegrabile și un sistem cu $2d-1$ ${\ Displaystyle 2d-1}$ ${\ Displaystyle 2d-1}$ Acesta a spus constante este maxim superintegrabile. ^[15] Deoarece soluția " ecuației Hamilton-Jacobi într - o coordonată a sistemului poate furniza numai $d$ ${\ displaystyle d}$ $d$ Constantele de mișcare, un sistem superintegrabile poate fi descompus în mai mult de un sistem de coordonate . ^[16] problema Kepler este cel mai superintegrabile, deoarece are trei grade de libertate $(d=3)$ ${\ Displaystyle (d = 3)}$ ${\ Displaystyle (d = 3)}$ și cinci constante independente ale mișcării; ecuația lui Hamilton-Jacobi este descompusă în ambele coordonate sferice , care , în coordonate parabolice . ^[17]

Sistemele superintegrabili urmeze Maximum o orbită închisă și unidimensional în spațiul de fază , deoarece orbita este dată de intersecția suprafeŃe de nivel dintre constantele mișcării. În consecință, orbitele sunt perpendiculare toate gradientilor tuturor acestor isosurfaces independente, cinci, în acest caz specific, și, prin urmare, sunt determinate de produsul vectorial generalizat al tuturor acestor gradienti. Ca urmare, toate sistemele sunt descrise automat superintegrabili prin mecanica Nambu ^[18] , sau, echivalent, de la mecanica Hamiltonian . Sistemele pot fi maximum superintegrabili cuantificați folosind relațiile comutative. ^[19] Cu toate acestea, într - o manieră echivalentă, ele pot fi cuantificați în setul de relații Nambu, ca și pentru problema clasică Kepler în atom de hidrogen ^[20] .

Evoluția în cadrul potențialelor perturbate

Figura 5: precesia treptată a unei orbite eliptice, cu excentricitate

e=0.667

{\ Displaystyle e = 0,667}

{\ Displaystyle e = 0,667}

. Acest precesiune își are originea în problema Kepler, dacă forța de atracție centrală deviază ușor de la pătratul. Precesia poate fi calculată cu ajutorul formulelor din text.

Laplace - vectorul Lenz - Runge $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ el este conservat doar într-o forță centrală cu proporționalitate pătratică inversă. In cele mai multe cazuri practice, cum ar fi mișcarea planetară, energia potențială a interacțiunii dintre cele două corpuri nu corespund întocmai legii pătratul, dar poate include o forță centrală suplimentară numită perturbație și descris de o energie potențială a tipului $h(r)$ ${\ H displaystyle (r)}$ ${\ H displaystyle (r)}$ . În aceste cazuri, Lenz se rotește încet vector în planul orbital, care corespunde unui fenomen matematic precesie orbita . Prin ipoteză, potențialul perturbând $h(r)$ ${\ H displaystyle (r)}$ ${\ H displaystyle (r)}$ Este o forță conservatoare centrală , ceea ce implică faptul că energia mecanică $ȘI$ ${\ displaystyle E}$ $ȘI$ și vectorul momentului cinetic $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ continuă să fie conservate. Prin urmare, mișcarea de minciuni încă în plan perpendicular la $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ și modulul de $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ este conservată conform ecuației $A^{2}=m^{2}k^{2}+2mEL^{2}$ ${\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2}}$ ${\ Displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2}}$ . Potențialul perturbare $h(r)$ ${\ H displaystyle (r)}$ ${\ H displaystyle (r)}$ acesta poate fi orice tip de funcție, dar ar trebui să fie semnificativ mai slabă decât forța de sine care unește cele două organisme.

Valoarea prin care se rotește vectorului Lenz oferă informații despre potențialul $h(r)$ ${\ H displaystyle (r)}$ ${\ H displaystyle (r)}$ . Este usor de demonstrat , folosind teoria obișnuită perturbatiilor și coordonatele de acțiune-unghi ^[1] , care $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ se rotește în ritmul

{\begin{array}{rcl}{\frac {\partial }{\partial L}}\langle h(r)\rangle &=&\displaystyle {\frac {\partial }{\partial L}}\left\{{\frac {1}{T}}\int _{0}^{T}h(r)\,dt\right\}\\[1em]&=&\displaystyle {\frac {\partial }{\partial L}}\left\{{\frac {m}{L^{2}}}\int _{0}^{2\pi }r^{2}h(r)\,d\theta \right\}.\end{array}}

{\ Displaystyle {\ begin {array} {RCL} {\ frac {\ parțial} {\ L parțială}} \ Langle h (r) \ rangle & = & \ displaystyle {\ frac {\ parțial} {\ L parțial} } \ stângă \ {{\ frac {1} {T}} \ int _ {0} ^ {T} h (r) \, dt \ dreapta \} \\ [1em] & = & \ displaystyle {\ frac { \ parțial} {\ L parțială}} \ left \ {{\ frac {m} {L ^ {2}}} \ int _ {0} ^ {2 \ pi} r ^ {2} h (r) \, d \ theta \ drept \}. \ end {array}}}

{\ Displaystyle {\ begin {array} {RCL} {\ frac {\ parțial} {\ L parțială}} \ Langle h (r) \ rangle & = & \ displaystyle {\ frac {\ parțial} {\ L parțial} } \ stângă \ {{\ frac {1} {T}} \ int _ {0} ^ {T} h (r) \, dt \ dreapta \} \\ [1em] & = & \ displaystyle {\ frac { \ parțial} {\ L parțială}} \ left \ {{\ frac {m} {L ^ {2}}} \ int _ {0} ^ {2 \ pi} r ^ {2} h (r) \, d \ theta \ drept \}. \ end {array}}}

unde este $T.$ ${\ displaystyle T}$ $T.$ este perioada orbitală și identitatea $Ldt=mr^{2}d\theta$ ${\ Displaystyle Ldt = mr ^ {2} d \ theta}$ ${\ Displaystyle Ldt = mr ^ {2} d \ theta}$ este utilizat pentru a converti integralei în timp la o integrală peste unghiul (Figura 5). Expresia din paranteze unghiulare, $\left\langle {h(r)}\right\rangle$ ${\ Displaystyle \$ din $stânga \ Langle {h (r)} \ dreapta \ rangle}$ ${\ Displaystyle \ din stânga \ Langle {h (r)} \ dreapta \ rangle}$ , Reprezintă potențialul perturbativa exprimat ca medie pe o perioadă întreagă, adică, peste un întreg pasaj a corpului în jurul orbitei sale. Matematic, această dată corespunde mediei cu suma următoare în acolade. Acest lucru ajută la fluctuațiile de mediere în viteza de rotație suprima.

Această abordare a fost utilizată pentru a ajuta la verificarea teoriei lui Einstein a relativității generale , care adaugă o mică perturbație invers cub de proporționalitate la gravitatea newtonian normale. ^[21]

h(r)={\frac {kL^{2}}{m^{2}c^{2}}}\left({\frac {1}{r^{3}}}\right)

{\ Displaystyle h (r) = {\ frac {kl ^ {2}} {m ^ {2} c ^ {2}}} \ stânga ({\ frac {1} {r ^ {3}}} \ dreapta )}

{\ Displaystyle h (r) = {\ frac {kl ^ {2}} {m ^ {2} c ^ {2}}} \ stânga ({\ frac {1} {r ^ {3}}} \ dreapta )}

Prin introducerea acestei funcții în integralei și folosind ecuația

{\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)

{\ Displaystyle {\ frac {1} {r}} = {\ frac {mk} {L ^ {2}}} \ stânga (1 + {\ frac {A} {mk}} \ cos \ theta \ dreapta) }

{\ Displaystyle {\ frac {1} {r}} = {\ frac {mk} {L ^ {2}}} \ stânga (1 + {\ frac {A} {mk}} \ cos \ theta \ dreapta) }

a exprima $r$ ${\ displaystyle r}$ $r$ în ceea ce privește $\theta$ ${\ displaystyle \ theta}$ $\ theta$ Precesia periapside cauzate de această perturbație non-newtoniene se dovedește a fi ^[21]

{\frac {6\pi k^{2}}{TL^{2}c^{2}}}

{\ Displaystyle {\ frac {6 \ pi k ^ {2}} {TL ^ {2} c ^ {2}}}}

{\ Displaystyle {\ frac {6 \ pi k ^ {2}} {TL ^ {2} c ^ {2}}}}

care se potrivește perfect cu precesia anormale observate empiric pentru planeta Mercur ^[22] și pulsar binar ^[23] . Acest acord cu experimentul este considerat o dovadă empirică puternică a relativității generale . ^[24] ^[25]

Paranteză lui Poisson

Cele trei componente $L_{i}$ ${\ L_ displaystyle {i}}$ ${\ L_ displaystyle {i}}$ a vectorului momentului unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ au un paranteze Poisson ^[1]

\left\{L_{i},L_{j}\right\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}

{\ Displaystyle \

din

stânga \ {L_ {i}, {L_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

{\ Displaystyle \ din stânga \ {L_ {i}, {L_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

unde este $i=1,2,3$ ${\ Displaystyle i = 1,2,3}$ $i = 1,2,3$ și $\varepsilon _{ijs}$ ${\ Displaystyle \ varepsilon _ {IJS}}$ ${\ Displaystyle \ varepsilon _ {IJS}}$ este simbolul Levi-Civita ; indicele $s$ ${\ displaystyle s}$ $s$ însumare este folosit aici pentru a se evita confuzia cu parametrul forță $k$ ${\ displaystyle k}$ $k$ definit anterior . Parantezele Poisson sunt reprezentate aici ca aparat dentar (nu pătrat), atât pentru coerența cu textele de referință , care la confuzii se evita contactul cu suportul Lie a mecanicii cuantice.

Așa cum va fi notat mai târziu, o variantă scalată a vectorului Lenz $\mathbf {D}$ ${\ displaystyle \ mathbf {D}}$ $\ mathbf D$ Ea poate fi definită cu aceleași unități de moment unghiular dividend $\mathbf {A}$ ${\ displaystyle \ mathbf {A}}$ $\ mathbf A$ pentru $p_{0}$ ${\ displaystyle p_ {0}}$ $p_ {0}$ . Cele parantezele Poisson de $\mathbf {D}$ ${\ displaystyle \ mathbf {D}}$ $\ mathbf D$ cu impuls unghiular $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ pot fi scrise într - o formă similară ^[26]

\left\{D_{i},L_{j}\right\}=\sum _{s=1}^{3}\varepsilon _{ijs}D_{s}

{\ Displaystyle \

din

stânga \ {D_ {i}, {L_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} D_ {s}}

{\ Displaystyle \ din stânga \ {D_ {i}, {L_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} D_ {s}}

Parantezele Poisson de $\mathbf {D}$ ${\ displaystyle \ mathbf {D}}$ $\ mathbf D$ cu sine depinde de semnul energiei mecanice $ȘI$ ${\ displaystyle E}$ $ȘI$ și, prin urmare, de faptul că orbita descrisă este deschis sau închis. Pentru o energie mecanică negativă -, prin urmare, pentru o orbită închisă - parantezele Poisson sunt exprimate ca

\left\{D_{i},D_{j}\right\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}

{\ Displaystyle \

din

stânga \ {D_ {i}, {D_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

{\ Displaystyle \ din stânga \ {D_ {i}, {D_ j} \ dreapta \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

în caz contrar, pentru energii pozitive pe care le arată semnul opus

\left\{D_{i},D_{j}\right\}=-\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}

{\ Displaystyle \

din

stânga \ {D_ {i}, {D_ j} \ dreapta \} = - \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

{\ Displaystyle \ din stânga \ {D_ {i}, {D_ j} \ dreapta \} = - \ sum _ {s = 1} ^ {3} \ varepsilon _ {IJS} L_ {s}}

L ' invariant Casimir pentru energia negativă este definită prin formula

C_{1}=\mathbf {D} \cdot \mathbf {D} +\mathbf {L} \cdot \mathbf {L} ={\frac {mk^{2}}{2\left|E\right|}}

{\ Displaystyle C_ {1} = \ mathbf {D} \ cdot \ mathbf {D} + \ mathbf {L} \ cdot \ mathbf {L} = {\ frac {mk ^ {2}} {2 \

din

stânga | E \ dreapta |}}}

{\ Displaystyle C_ {1} = \ mathbf {D} \ cdot \ mathbf {D} + \ mathbf {L} \ cdot \ mathbf {L} = {\ frac {mk ^ {2}} {2 \ din stânga | E \ dreapta |}}}

C_{2}=\mathbf {D} \cdot \mathbf {L} =0

{\ C_ displaystyle {2} = \ mathbf {D} \ cdot \ mathbf {L} = 0}

{\ C_ displaystyle {2} = \ mathbf {D} \ cdot \ mathbf {L} = 0}

și are zero paranteze Poisson cu fiecare componentă $\mathbf {D}$ ${\ displaystyle \ mathbf {D}}$ $\ mathbf D$ sau $\mathbf {L}$ ${\ displaystyle \ mathbf {L}}$ ${\ mathbf L}$ :

\left\{C_{1},L_{i}\right\}=\left\{C_{1},D_{i}\right\}=\left\{C_{2},L_{i}\right\}=\left\{C_{2},D_{i}\right\}=0

{\ Displaystyle \

din

stânga \ {C_ {1}, L_ {i} \ dreapta \} = \

din

stânga \ {C_ {1}, D_ {i} \ dreapta \} = \

din

stânga \ {C_ {2}, L_ { i} \ dreapta \} = \

din

stânga \ {C_ {2}, D_ {i} \ dreapta \} = 0}

{\ Displaystyle \ din stânga \ {C_ {1}, L_ {i} \ dreapta \} = \ din stânga \ {C_ {1}, D_ {i} \ dreapta \} = \ din stânga \ {C_ {2}, L_ { i} \ dreapta \} = \ din stânga \ {C_ {2}, D_ {i} \ dreapta \} = 0}

.

$C_{2}$ ${\ displaystyle C_ {2}}$ $C_ {2}$ ea este în mod evident la zero, astfel încât cei doi vectori sunt întotdeauna perpendiculare. Cu toate acestea, celălalt este invariantă $C_{1}$ ${\ displaystyle C_ {1}}$ $C_ {1}$ nu este evidentă și doar depinde de $m, k$ ${\ Displaystyle m, k}$ ${\ Displaystyle m, k}$ și $ȘI$ ${\ displaystyle E}$ $ȘI$ . Acest invariant ajută să derive nivelele de energie ale unui atom de hidrogen , cum ar fi folosind doar mecanicii cuantice canonice, în loc de mai complexe ecuația Schrödinger .

Spectru de energie al atomului de hidrogen

Figura 6: Nivelurile de energie ale atomului de hidrogen prezis de relațiile de comutare între momentul cinetic și vectorul Lenz; această configurație a fost verificată experimental.

Același subiect în detaliu: atom de hidrogen .

Le parentesi di Poisson sono un utile strumento per studiare lo spettro di energia dell'atomo di idrogeno, e più in generale forniscono un semplice metodo di quantizzazione canonica dei sistemi dinamici; le relazioni di commutazione fra due operatori quantistici corrispondono alle parentesi di Poisson delle corrispondenti variabili classiche moltiplicate per $i\hbar$ $i\hbar$ $i\hbar$ . ^[27] Portando a termine questa quantizzazione e calcolando il valore dell'operatore di Casimir $C_{1}$ $C_{1}$ $C_{{1}}$ per il problema di Keplero, Wolfgang Pauli riuscì a derivare lo spettro di energia di un atomo idrogenoide (Figura 6) e, di conseguenza, lo spettro di emissione. ^[3] Questa elegante derivazione fu ottenuta prima dello sviluppo del concetto di funzione d'onda . ^[28]

Una sottigliezza dell'operatore quantistico per il vettore di Lenz $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ è che gli operatori momento e momento angolare non commutano fra loro; dunque, il prodotto vettoriale di $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ ed $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ deve essere definito con cura. ^[26] Tipicamente, gli operatori per le componenti cartesiane $A_{s}$ $A_{s}$ $A_{s}$ sono definiti utilizzando un prodotto simmetrico:

A_{s}=-mk{\hat {r}}_{s}+{\frac {1}{2}}\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{sij}\left(p_{i}l_{j}+l_{j}p_{i}\right)

A_{s}=-mk{\hat {r}}_{s}+{\frac {1}{2}}\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{sij}\left(p_{i}l_{j}+l_{j}p_{i}\right)

A_{s}=-mk{\hat {r}}_{s}+{\frac {1}{2}}\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{sij}\left(p_{i}l_{j}+l_{j}p_{i}\right)

da cui i corrispondenti operatori di scala possono essere definiti come:

J_{0}=A_{3}\,

J_{0}=A_{3}\,

J_{0}=A_{3}\,

J_{\pm 1}=\mp {\frac {1}{\sqrt {2}}}\left(A_{1}\pm iA_{2}\right)

J_{\pm 1}=\mp {\frac {1}{\sqrt {2}}}\left(A_{1}\pm iA_{2}\right)

J_{\pm 1}=\mp {\frac {1}{\sqrt {2}}}\left(A_{1}\pm iA_{2}\right)

Un primo operatore per l'invariante di Casimir può così essere definito

C_{1}=-{\frac {mk^{2}}{2\hbar ^{2}}}H^{-1}-I

C_{1}=-{\frac {mk^{2}}{2\hbar ^{2}}}H^{-1}-I

C_{1}=-{\frac {mk^{2}}{2\hbar ^{2}}}H^{-1}-I

dove $H^{-1}$ $H^{-1}$ $H^{-1}$ è l'inverso dell'operatore Hamiltoniano dell'energia ed $I$ ${\displaystyle I}$ $I$ è l' operatore identità . Applicando questi operatori di scala agli stati $\left|lmn\right.\rangle$ $\left|lmn\right.\rangle$ $\left|lmn\right.\rangle$ degli operatori del momento angolare totale, momento angolare azimutale e dell'energia, i valori del primo operatore di Casimir $C_{1}$ $C_{1}$ $C_{1}$ sono $n^{2}-1$ $n^{2}-1$ $n^{2}-1$ ; cosa notevole, essi sono indipendenti dai numeri quantici $l$ ${\displaystyle l}$ $l$ ed $m$ ${\displaystyle m}$ $m$ , rendendo i livelli energetici degeneri. ^[26] In definitiva, i livelli energetici sono dati da:

E_{n}=-{\frac {mk^{2}}{2\hbar ^{2}n^{2}}}

E_{n}=-{\frac {mk^{2}}{2\hbar ^{2}n^{2}}}

E_{n}=-{\frac {mk^{2}}{2\hbar ^{2}n^{2}}}

che corrisponde alla Formula di Rydberg per l'atomo idrogenoide (Figura 6).

Conservazione e simmetria

La conservazione del vettore di Lenz corrisponde a una sottile simmetria del sistema. In meccanica classica , le simmetrie sono operazioni continue che trasformano un'orbita in un'altra senza mutare l'energia meccanica del sistema; in meccanica quantistica , le simmetrie diventano invece operazioni continue che "miscelano" orbitali atomici dotati della stessa energia. Una quantità conservata è usualmente associata a queste simmetrie. ^[1] Per esempio, ogni forza centrale è simmetrica rispetto al gruppo delle rotazioni in tre dimensioni SO(3), portando alla conservazione del momento angolare $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ . In meccanica classica , una rotazione totale del sistema non può variare l'energia dell'orbita; in meccanica quantistica, le rotazioni miscelano le armoniche sferiche aventi stesso numero quantico $l$ ${\displaystyle l}$ $l$ senza variazioni di energia.

Figura 7: Le famiglie di odografi del momento aventi la stessa energia

E

{\displaystyle E}

E

. Tutte le circonferenze passano per gli stessi due punti

\pm p_{0}=\pm {\sqrt {2m\left|E\right|}}

\pm p_{0}=\pm {\sqrt {2m\left|E\right|}}

\pm p_{0}=\pm {\sqrt {2m\left|E\right|}}

sull'asse

p_{x}

p_{x}

p_{x}

(vedi Figura 3).

La simmetria per una forza centrale rispondente alla legge dell'inverso del quadrato è più profonda e sottile; la peculiare simmetria di questi problemi dà come risultato sia la conservazione del momento angolare $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ e del vettore di Lenz $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ ed, in meccanica quantistica , assicura che i livelli energetici dell'idrogeno non dipendano dai numeri quantici del momento angolare $l$ ${\displaystyle l}$ $l$ ed $m$ ${\displaystyle m}$ $m$ . La simmetria è comunque più sottile, tuttavia, poiché le operazioni di simmetria devono essere rappresentate in uno spazio quadri-dimensionale, queste particolari simmetrie vengono spesso definite "simmetrie nascoste". In meccanica classica , l'alta simmetria dei problemi di Keplero permette l'esistenza di trasformazioni continue dell'orbita che conservano l'energia meccanica ma non il momento angolare, detto in altre parole, orbite della stessa energia ma diverso momento angolare (e quindi diversa eccentricità) possono essere trasformate simmetricamente l'una nell'altra. Quantisticamente parlando, ciò corrisponde a mischiare orbitali che differiscono per i numeri quantici $l$ ${\displaystyle l}$ $l$ ed $m$ ${\displaystyle m}$ $m$ , come per quel che riguarda gli orbitali $s$ ${\displaystyle s}$ $s$ (aventi $l=0$ ${\displaystyle l=0}$ $l=0$ ) e $p$ ${\displaystyle p}$ $p$ (aventi $l=1$ ${\displaystyle l=1}$ $l=1$ ). Queste trasformazioni non possono essere effettuate attraverso ordinarie traslazioni e rotazioni nello spazio euclideo tridimensionale, ma risultano invece equivalenti a una rotazione in più dimensioni.

Per energie meccaniche negative (orbite chiuse), il gruppo di simmetria più elevato è SO(4), che conserva il modulo dei vettori quadridimensionali

\left|\mathbf {e} \right|^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2}

\left|\mathbf {e} \right|^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2}

\left|\mathbf {e} \right|^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2}

Nel 1935 , Vladimir Fock dimostrò che i problemi di Keplero quantistici ad energia negativa sono equivalenti allo studio di una particella libera confinata in una superficie sferica tridimensionale dentro ad uno spazio quadri-dimensionale. ^[4] Specificatamente, Fock mostrò che la funzione d'onda di Schrödinger nello spazio del momento per il problema di Keplero corrispondeva alla proiezione stereografica dell' armonica sferica sulla sfera. Rotazioni di questa sfera e riproiezioni risultano in una continua variazione dell'orbita ellittica senza alcun cambiamento nell'energia totale; in termini quantistici, ciò corrisponde ad uno scambio di orbitali con lo stesso numero quantico di energia $n$ ${\displaystyle n}$ $n$ . Valentine Bargman notò conseguentemente che le parentesi di Poisson per il vettore momento angolare $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ ed il vettore di Lenz scalato $\mathbf {D}$ $\mathbf {D}$ $\mathbf D$ formano un' algebra di Lie per il gruppo di simmetria SO(4). ^[5] Detto semplicemente, le sei quantità $\mathbf {D}$ $\mathbf {D}$ $\mathbf D$ ed $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ corrispondono a sei momenti angolari conservati in quattro dimensioni, associati a sei possibili rotazioni semplici SO(4) in questo spazio (esistono infatti sei modi per scegliere due assi fra quattro). Questa conclusione non implica che il nostro universo sia una sfera tridimensionale, semplicemente implica che questo particolare sistema fisico è matematicamente equivalente a una particella libera su una sfera tridimensionale.

Per energie meccaniche positive (sistemi non legati) il gruppo di simmetria più elevato è SO(3,1), che preserva il modulo di Minkowski del quadrivettore

ds^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}-e_{4}^{2}

ds^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}-e_{4}^{2}

ds^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}-e_{4}^{2}

.

Entrambi i casi a energia positiva e negativa furono considerati nel lavoro di Fock ^[4] e rivisti enciclopedicamente da Bander e Itzykson . ^[29] ^[30]

Le orbite di un sistema sottoposto a una forza centrale (che risponde alla legge dell'inverso del quadrato) sono anche simmetriche nelle riflessioni . Dunque, i gruppi SO(3), SO(4) ed SO(3,1) citati sopra non corrispondono alla serie completa dei gruppi di simmetria di queste orbite; i gruppi completi sono i gruppi ortogonali O(3), O(4) ed O(3,1), rispettivamente. Nondimeno, solo i sottogruppi SO(3), SO(4) ed SO(3,1) sono necessari per dimostrare la conservazione del momento angolare e del vettore di Lenz; la simmetria per riflessione è irrilevante per le conservazioni, che possono essere derivate dell' algebra di Lie del gruppo.

Simmetrie di rotazione in quattro dimensioni

Figura 8: l'odografo del momento in Figura 7 corrisponde alla proiezione stereografica dei cerchi massimi sulla sfera tridimensionale unitaria

\eta

\eta

\eta

. Tutti i cerchi massimi intersecano l'asse

\eta _{x}

\eta _{x}

\eta _{x}

, che è perpendicolare alla pagina; la proiezione è dal polo Nord (il vettore unitario

\mathbf {w}

\mathbf {w}

\mathbf w

) al piano

\eta _{x}-\eta _{y}

\eta _{x}-\eta _{y}

\eta _{x}-\eta _{y}

, come mostrato qui per l'odografo magenta dalle linee nere tratteggiate. Il cerchio massimo a latitudine

\alpha

\alpha

\alpha

corrisponde al vettore eccentricità secondo l'equazione

e=\sin \alpha

e=\sin \alpha

e=\sin \alpha

. I colori dei cerchi massimi mostrati qui corrispondono a quelli dei loro corrispondenti odografi in figura 7.

La connessione fra il Problema dei due corpi e la simmetria rotazionale in quattro dimensioni SO(4) può essere visualizzato efficacemente. ^[29] ^[31] ^[32] Si determinino le quattro coordinate cartesiane $w, x, y, z$ ${\displaystyle w,x,y,z}$ $w,x,y,z$ , dove $x, y, z$ ${\displaystyle x,y,z}$ $x,y,z$ rappresentano le coordinate del normale vettore posizione $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ . Il vettore tridimensionale momento $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ è associato ad un vettore quadridimensionale ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ su una sfera tridimensionale unitaria

{\begin{array}{rcl}{\boldsymbol {\eta }}&=&\displaystyle {\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0}^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\[1em]&=&\displaystyle {\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\mathbf {p} \end{array}}

{\begin{array}{rcl}{\boldsymbol {\eta }}&=&\displaystyle {\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0}^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\[1em]&=&\displaystyle {\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\mathbf {p} \end{array}}

{\begin{array}{rcl}{\boldsymbol {\eta }}&=&\displaystyle {\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0}^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\[1em]&=&\displaystyle {\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\mathbf {p} \end{array}}

,

dove $\mathbf {\hat {w}}$ $\mathbf {\hat {w}}$ $\mathbf {\hat {w}}$ è il vettore unitario lungo il nuovo asse $w$ ${\displaystyle w}$ $w$ . La trasformazione che converte $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ in $\mathbf {\eta }$ $\mathbf {\eta }$ $\mathbf {\eta }$ può essere invertita univocamente, per esempio, la componente $x$ ${\displaystyle x}$ $x$ del momento è data da:

p_{x}=p_{0}{\frac {\eta _{x}}{1-\eta _{w}}}

p_{x}=p_{0}{\frac {\eta _{x}}{1-\eta _{w}}}

p_{x}=p_{0}{\frac {\eta _{x}}{1-\eta _{w}}}

e similmente per $p_{y}$ $p_{y}$ $p_{y}$ e $p_{z}$ $p_{z}$ $p_{z}$ . In altre parole, il vettore tridimensionale $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ è una proiezione stereografica del vettore quadri-dimensionale ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ , scalato per $p_{0}$ $p_{0}$ $p_{0}$ (Figura 8).

Senza perdere di generalità, noi possiamo eliminare la normale simmetria rotazionale imponendo le coordinate cartesiane in modo che l'asse $z$ ${\displaystyle z}$ $z$ sia allineato con il vettore momento angolare $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ e gli odografi del momento siano allineati così come lo sono in Figura 7, con i centri delle circonferenze sull'asse $y$ ${\displaystyle y}$ $y$ . Poiché il moto è planare e $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ ed $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ sono perpendicolari, $p_{z}=\eta _{z}=0$ $p_{z}=\eta _{z}=0$ $p_{z}=\eta _{z}=0$ , l'attenzione dovrebbe essere limitata al vettore tridimensionale ${\boldsymbol {\eta }}=(\eta _{w},\eta _{x},\eta _{y})$ ${\boldsymbol {\eta }}=(\eta _{w},\eta _{x},\eta _{y})$ ${\boldsymbol {\eta }}=(\eta _{w},\eta _{x},\eta _{y})$ . La famiglia di cerchi di Apollonio degli odografi del momento (Figura 7) corrisponde a una famiglia di cerchi massimi sulla sfera tridimensionale ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ , ognuno dei quali interseca l'asse $\eta _{x}$ $\eta _{x}$ $\eta _{x}$ nei due punti $\eta _{x}=\pm 1$ $\eta _{x}=\pm 1$ $\eta _{x}=\pm 1$ , corrispondenti ai punti degli odografi in $p_{x}=\pm p_{0}$ $p_{x}=\pm p_{0}$ $p_{x}=\pm p_{0}$ . Questi cerchi massimi sono legati da una semplice relazione riguardante l'asse $\eta _{x}$ $\eta _{x}$ $\eta _{x}$ (Figura 8). Questa simmetria di rotazione trasforma tutte le orbite della stessa energia in un'altra, tuttavia, una tale rotazione è ortogonale alle usuali rotazioni tridimensionali, poiché trasforma la quarta dimensione $\eta _{w}$ $\eta _{w}$ $\eta _{w}$ . Questa maggiore simmetria è una caratteristica del problema dei due corpi e corrisponde alla conservazione del vettore di Lenz.

Un'elegante soluzione in variabili angolo-azione per il problema di Keplero può essere ottenuta eliminando le ridondanti coordinate quadridimensionali ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ ${\boldsymbol {\eta }}$ in favore di un sistema di coordinate ellittico-cilindriche $(\chi ,\psi ,\varphi )$ $(\chi ,\psi ,\varphi )$ $(\chi ,\psi ,\varphi )$ ^[33]

\eta _{w}=\mathrm {cn} \,\chi \ \mathrm {cn} \,\psi

\eta _{w}=\mathrm {cn} \,\chi \ \mathrm {cn} \,\psi

\eta _{w}=\mathrm {cn} \,\chi \ \mathrm {cn} \,\psi

\eta _{x}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \cos \phi

\eta _{x}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \cos \phi

\eta _{x}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \cos \phi

\eta _{y}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \sin \phi

\eta _{y}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \sin \phi

\eta _{y}=\mathrm {sn} \,\chi \ \mathrm {dn} \,\psi \ \sin \phi

\eta _{z}=\mathrm {dn} \,\chi \ \mathrm {sn} \,\psi

\eta _{z}=\mathrm {dn} \,\chi \ \mathrm {sn} \,\psi

\eta _{z}=\mathrm {dn} \,\chi \ \mathrm {sn} \,\psi

dove $s n, c n$ ${\displaystyle sn,cn}$ $sn,cn$ e $d n$ ${\displaystyle dn}$ $dn$ sono le Funzioni ellittiche di Jacobi .

Generalizzazione ad altri potenziali e relatività

il vettore di Lenz può anche essere generalizzato allo scopo di identificare quantità conservate applicabili in situazioni diverse da quelle sopra descritte.

In presenza di un campo elettrico $\mathbf {E}$ $\mathbf {E}$ $\mathbf E$ , il vettore di Lenz generalizzato (e conservato) ${\mathcal {A}}$ ${\mathcal {A}}$ ${\mathcal {A}}$ è ^[17] ^[34]

{\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \right)\times \mathbf {r} \right]

{\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \right)\times \mathbf {r} \right]

{\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \right)\times \mathbf {r} \right]

,

dove $q$ ${\displaystyle q}$ $q$ è la carica elettrica della particella orbitante.

Generalizzando ulteriormente il vettore di Lenz ad altri potenziali ed alla relatività speciale , si ottiene la forma più generale e scritta come ^[7]

{\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \right)+\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\right)\right]L^{2}\mathbf {\hat {r}}

{\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \right)+\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\right)\right]L^{2}\mathbf {\hat {r}}

{\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \right)+\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\right)\right]L^{2}\mathbf {\hat {r}}

dove $u={\frac {1}{r}}$ $u={\frac {1}{r}}$ $u={\frac {1}{r}}$ (ved. teorema di Bertrand ) e $\xi =\cos \theta$ $\xi =\cos \theta$ $\xi =\cos \theta$ , con l'angolo $\theta$ $\theta$ $\theta$ definito da:

\theta =L\int ^{u}{\frac {du}{\sqrt {m^{2}c^{2}\left(\gamma ^{2}-1\right)-L^{2}u^{2}}}}

\theta =L\int ^{u}{\frac {du}{\sqrt {m^{2}c^{2}\left(\gamma ^{2}-1\right)-L^{2}u^{2}}}}

\theta =L\int ^{u}{\frac {du}{\sqrt {m^{2}c^{2}\left(\gamma ^{2}-1\right)-L^{2}u^{2}}}}

e $\gamma$ $\gamma$ $\gamma$ è il Fattore di Lorentz . Come osservato precedentemente, si può ottenere un vettore conservato binormale $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ eseguendo il prodotto vettoriale con il vettore momento angolare:

{\mathcal {B}}=\mathbf {L} \times {\mathcal {A}}

{\mathcal {B}}=\mathbf {L} \times {\mathcal {A}}

{\mathcal {B}}=\mathbf {L} \times {\mathcal {A}}

Questi due vettori possono essere combinati per formare un tensore diadico $\mathbf {W}$ $\mathbf {W}$ $\mathbf {W}$ :

{\mathcal {W}}=\alpha {\mathcal {A}}\otimes {\mathcal {A}}+\beta \,{\mathcal {B}}\otimes {\mathcal {B}}

{\mathcal {W}}=\alpha {\mathcal {A}}\otimes {\mathcal {A}}+\beta \,{\mathcal {B}}\otimes {\mathcal {B}}

{\mathcal {W}}=\alpha {\mathcal {A}}\otimes {\mathcal {A}}+\beta \,{\mathcal {B}}\otimes {\mathcal {B}}

Per esempio, è possibile calcolare il vettore di Lenz per un oscillatore armonico isotropo e non relativistico. ^[7] Poiché la forza è centrale

\mathbf {F} (r)=-k\mathbf {r}

\mathbf {F} (r)=-k\mathbf {r}

\mathbf {F} (r)=-k\mathbf {r}

il vettore momento angolare è conservato ed il moto giace in un piano. Il tensore diadico conservato può essere scritto in una semplice forma:

{\mathcal {W}}={\frac {1}{2m}}\mathbf {p} \otimes \mathbf {p} +{\frac {k}{2}}\,\mathbf {r} \otimes \mathbf {r}

{\mathcal {W}}={\frac {1}{2m}}\mathbf {p} \otimes \mathbf {p} +{\frac {k}{2}}\,\mathbf {r} \otimes \mathbf {r}

{\mathcal {W}}={\frac {1}{2m}}\mathbf {p} \otimes \mathbf {p} +{\frac {k}{2}}\,\mathbf {r} \otimes \mathbf {r}

inoltre si può notare che $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ ed $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ non sono necessariamente perpendicolari. Il vettore di Lenz corrispondente è più complicato:

{\mathcal {A}}={\frac {1}{\sqrt {mr^{2}\omega _{0}A-mr^{2}E+L^{2}}}}\left\{\left(\mathbf {p} \times \mathbf {L} \right)+\left(mr\omega _{0}A-mrE\right)\mathbf {\hat {r}} \right\}

{\mathcal {A}}={\frac {1}{\sqrt {mr^{2}\omega _{0}A-mr^{2}E+L^{2}}}}\left\{\left(\mathbf {p} \times \mathbf {L} \right)+\left(mr\omega _{0}A-mrE\right)\mathbf {\hat {r}} \right\}

{\mathcal {A}}={\frac {1}{\sqrt {mr^{2}\omega _{0}A-mr^{2}E+L^{2}}}}\left\{\left(\mathbf {p} \times \mathbf {L} \right)+\left(mr\omega _{0}A-mrE\right)\mathbf {\hat {r}} \right\}

dove $\omega _{0}={\sqrt {\frac {k}{m}}}$ $\omega _{0}={\sqrt {\frac {k}{m}}}$ $\omega _{0}={\sqrt {\frac {k}{m}}}$ è la frequenza naturale dell'oscillatore ed $A=(E^{2}-\omega ^{2}L^{2})^{1/2}/\omega$ $A=(E^{2}-\omega ^{2}L^{2})^{1/2}/\omega$ $A=(E^{2}-\omega ^{2}L^{2})^{1/2}/\omega$ .

Prove che il vettore di Lenz risulta conservato nei problemi di Keplero

I seguenti sono argomenti atti a dimostrare che il vettore di Lenz è conservato in campi di forze centrali che obbediscono alla legge dell'inverso del quadrato.

Prove dirette della conservazione

Una forza centrale $\mathbf {F}$ $\mathbf {F}$ $\mathbf{F}$ agente su una particella è:

\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}}

\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}}

\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}}

per alcune funzioni $f(r)$ ${\displaystyle f(r)}$ $f(r)$ del raggio $r$ ${\displaystyle r}$ $r$ . Poiché il momento angolare $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ è conservato in una forza centrale, ${\frac {d}{dt}}\mathbf {L} =0$ ${\frac {d}{dt}}\mathbf {L} =0$ ${\frac {d}{dt}}\mathbf {L} =0$ e

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right]

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right]

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right]

dove il momento $\mathbf {p} =m{\frac {d\mathbf {r} }{dt}}$ $\mathbf {p} =m{\frac {d\mathbf {r} }{dt}}$ $\mathbf {p} =m{\frac {d\mathbf {r} }{dt}}$ ed il triplo prodotto vettoriale è stato semplificato utilizzando la formula di Lagrange

\mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\right)=\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}

\mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\right)=\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}

\mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\right)=\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}

.

L'identità

{\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \right)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}\left(r^{2}\right)=2r{\frac {dr}{dt}}

{\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \right)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}\left(r^{2}\right)=2r{\frac {dr}{dt}}

{\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \right)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}\left(r^{2}\right)=2r{\frac {dr}{dt}}

porta all'equazione:

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)

per il caso speciale di una forza centrale che risponde alla legge dell'inverso del quadrato $f(r)={\frac {-k}{r^{2}}}$ $f(r)={\frac {-k}{r^{2}}}$ $f(r)={\frac {-k}{r^{2}}}$ , questo è uguale a:

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=mk{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)={\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=mk{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)={\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)

{\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=mk{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)={\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)

.

Dunque, $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ è conservato in questo tipo di forze:

{\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)-{\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)=\mathbf {0}

{\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)-{\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)=\mathbf {0}

{\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)-{\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)=\mathbf {0}

.

Come descritto sopra , questo vettore di Lenz $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ è un caso speciale del vettore generalizzato ${\mathcal {A}}$ ${\mathcal {A}}$ ${\mathcal {A}}$ che può essere definito per tutte le forze centrali . ^[7] ^[8] Tuttavia, poiché molte forze centrali non producono orbite chiuse (vedi Teorema di Bertrand , l'analogo vettore ${\mathcal {A}}$ ${\mathcal {A}}$ ${\mathcal {A}}$ raramente possiede una semplice definizione ed è generalmente una funzione funzione polidroma dell'angolo $\theta$ $\theta$ $\theta$ fra $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ e ${\mathcal {A}}$ ${\mathcal {A}}$ ${\mathcal {A}}$ .

Equazioni di Hamilton–Jacobi in coordinate paraboliche

La conservazione del vettore di Lenz può essere anche derivata dalle Equazioni di Hamilton–Jacobi in coordinate paraboliche $(\xi ,\eta )$ $(\xi ,\eta )$ $(\xi ,\eta )$ , che sono definite attraverso le equazioni

\xi =r+x\,

\xi =r+x\,

\xi =r+x\,

\eta =r-x\,

\eta =rx\,

\eta =r-x\,

dove $r$ ${\displaystyle r}$ $r$ rappresenta il raggio nel piano dell'orbita

r={\sqrt {x^{2}+y^{2}}}

r={\sqrt {x^{2}+y^{2}}}

r={\sqrt {x^{2}+y^{2}}}

l'inversione di queste coordinate è:

x={\frac {1}{2}}\left(\xi -\eta \right)

x={\frac {1}{2}}\left(\xi -\eta \right)

x={\frac {1}{2}}\left(\xi -\eta \right)

y={\sqrt {\xi \eta }}

y={\sqrt {\xi \eta }}

y={\sqrt {\xi \eta }}

.

La separazione delle equazioni di Hamilton–Jacobi in queste coordinate porta a due equazioni equivalenti ^[17] ^[35]

2\xi p_{\xi }^{2}-mk-mE\xi =-\Gamma

2\xi p_{\xi }^{2}-mk-mE\xi =-\Gamma

2\xi p_{\xi }^{2}-mk-mE\xi =-\Gamma

2\eta p_{\eta }^{2}-mk-mE\eta =\Gamma

2\eta p_{\eta }^{2}-mk-mE\eta =\Gamma

2\eta p_{\eta }^{2}-mk-mE\eta =\Gamma

dove $\Gamma$ $\Gamma$ $\Gamma$ è una costante del moto . Sottraendo e re-esprimendo in termini del vettore momento $p_{x}$ $p_{x}$ $p_{x}$ e $p_{y}$ $p_{y}$ $p_{y}$ si dimostra che $\Gamma$ $\Gamma$ $\Gamma$ è equivalente al vettore di Lenz:

\Gamma =p_{y}\left(xp_{y}-yp_{x}\right)-mk{\frac {x}{r}}=A_{x}

\Gamma =p_{y}\left(xp_{y}-yp_{x}\right)-mk{\frac {x}{r}}=A_{x}

\Gamma =p_{y}\left(xp_{y}-yp_{x}\right)-mk{\frac {x}{r}}=A_{x}

.

Teorema di Noether

La connessione fra la simmetria rotazionale descritta sopra e la conservazione del vettore di Lenz può essere espressa quantitativamente attraverso il Teorema di Noether . Questo teorema, che è utilizzato per trovare costanti del moto, afferma che ogni variazione infinitesimale delle coordinate generalizzate del sistema fisico

\delta q_{i}=\varepsilon g_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t)

\delta q_{i}=\varepsilon g_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t)

\delta q_{i}=\varepsilon g_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t)

che porta la Lagrangiana del sistema a una variazione di primo ordine per una derivata totale sul tempo

\delta L=\varepsilon {\frac {d}{dt}}G(\mathbf {q} ,t)

\delta L=\varepsilon {\frac {d}{dt}}G(\mathbf {q} ,t)

\delta L=\varepsilon {\frac {d}{dt}}G(\mathbf {q} ,t)

corrisponde a una quantità conservata $\Gamma$ $\Gamma$ $\Gamma$ :

\Gamma =-G+\sum _{i}g_{i}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)

\Gamma =-G+\sum _{i}g_{i}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)

\Gamma =-G+\sum _{i}g_{i}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)

in particolare, la componente conservata del vettore di Lenz $A_{s}$ $A_{s}$ $A_{s}$ corrisponde alla variazione nelle coordinate ^[36]

\delta x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{is}\left(\mathbf {r} \cdot \mathbf {p} \right)\right]

\delta x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{is}\left(\mathbf {r} \cdot \mathbf {p} \right)\right]

\delta x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{is}\left(\mathbf {r} \cdot \mathbf {p} \right)\right]

,

dove $i=1,2,3$ ${\displaystyle i=1,2,3}$ $i=1,2,3$ , con $x_{i}$ $x_{i}$ $x_i$ e $p_{i}$ $p_{i}$ $p_{i}$ diventano le componenti $i-$ ${\displaystyle i-}$ $i-$ esime dei vettori posizione e momento $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ e $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ , rispettivamente; come usuale, $\delta _{is}$ $\delta _{is}$ $\delta _{is}$ rappresenta il delta di Kronecker . La corrispondente variazione di primo ordine nella Lagrangiana è:

\delta L=\varepsilon mk{\frac {d}{dt}}\left({\frac {x_{s}}{r}}\right)

\delta L=\varepsilon mk{\frac {d}{dt}}\left({\frac {x_{s}}{r}}\right)

\delta L=\varepsilon mk{\frac {d}{dt}}\left({\frac {x_{s}}{r}}\right)

.

Sostituzioni nella formula generale per la quantità conservata $\Gamma$ $\Gamma$ $\Gamma$ porta alla componente conservata $A_{s}$ $A_{s}$ $A_{s}$ del vettore di Lenz:

A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \right)\right]-mk\left({\frac {x_{s}}{r}}\right)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \right)\right]_{s}-mk\left({\frac {x_{s}}{r}}\right)

A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \right)\right]-mk\left({\frac {x_{s}}{r}}\right)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \right)\right]_{s}-mk\left({\frac {x_{s}}{r}}\right)

A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \right)\right]-mk\left({\frac {x_{s}}{r}}\right)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \right)\right]_{s}-mk\left({\frac {x_{s}}{r}}\right)

.

Trasformazioni di Lie

Figura 9: La trasformazione di Lie dalla quale è stata derivata del vettore di Lenz

\mathbf {A}

\mathbf {A}

\mathbf A

. Al variare del fattore di scala

\lambda

\lambda

\lambda

, cambiano l'energia ed il momento angolare, ma l'eccentricità

e

{\displaystyle e}

e

ed il modulo e la direzione di

\mathbf {A}

\mathbf {A}

\mathbf A

rimangono inalterati.

La derivazione della conservazione del vettore di Lenz $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ attraverso il teorema di Noether è elegante, ma ha un problema: la variazione delle coordinate $\delta x_{i}$ $\delta x_{i}$ $\delta x_{i}$ comporta non solo la posizione $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ , ma anche il momento $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ o, equivalentemente, la velocità $\mathbf {v}$ $\mathbf {v}$ $\mathbf v$ . ^[37] Questa complicazione può essere eliminata semplicemente derivando la conservazione di $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ utilizzando un altro approccio, impostato da Sophus Lie . ^[38] ^[39] Per la precisione, è possibile definire una trasformazione di Lie ^[40] in cui le coordinate $\mathbf {r}$ $\mathbf {r}$ $\mathbf r$ ed il tempo $t$ ${\displaystyle t}$ $t$ sono riscalati per differenti valori del parametro $\lambda$ $\lambda$ $\lambda$ (Figura 9)

t\rightarrow \lambda ^{3}t,\ \mathbf {r} \rightarrow \lambda ^{2}\mathbf {r} ,\ \mathbf {p} \rightarrow {\frac {1}{\lambda }}\mathbf {p}

t\rightarrow \lambda ^{3}t,\ \mathbf {r} \rightarrow \lambda ^{2}\mathbf {r} ,\ \mathbf {p} \rightarrow {\frac {1}{\lambda }}\mathbf {p}

t\rightarrow \lambda ^{3}t,\ \mathbf {r} \rightarrow \lambda ^{2}\mathbf {r} ,\ \mathbf {p} \rightarrow {\frac {1}{\lambda }}\mathbf {p}

questa trasformazione cambia il momento angolare totale $L$ ${\displaystyle L}$ $L$ e l'energia $E$ ${\displaystyle E}$ $E$

L\rightarrow \lambda L,\ E\rightarrow {\frac {1}{\lambda ^{2}}}E

L\rightarrow \lambda L,\ E\rightarrow {\frac {1}{\lambda ^{2}}}E

L\rightarrow \lambda L,\ E\rightarrow {\frac {1}{\lambda ^{2}}}E

ma conserva il loro prodotto $EL^{2}$ $EL^{2}$ $EL^{2}$ . Dunque, l'eccentricità $e$ ${\displaystyle e}$ $e$ e la grandezza $A$ ${\displaystyle A}$ $A$ sono conservate, come si può vedere dalle equazioni per $A^{2}$ $A^{2}$ $A^{2}$

A^{2}=m^{2}k^{2}e^{2}=m^{2}k^{2}+2mEL^{2}

A^{2}=m^{2}k^{2}e^{2}=m^{2}k^{2}+2mEL^{2}

A^{2}=m^{2}k^{2}e^{2}=m^{2}k^{2}+2mEL^{2}

la direzione di $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ è anch'essa conservata, poiché i semiassi non sono alterati da una riscala globale. Queste trasformazioni conservano anche la terza legge di Keplero , ovvero, il semiasse maggiore $a$ ${\displaystyle a}$ $a$ ed il periodo $T$ ${\displaystyle T}$ $T$ formano una costante ${\frac {T^{2}}{a^{3}}}$ ${\frac {T^{2}}{a^{3}}}$ ${\frac {T^{2}}{a^{3}}}$ .

Fattori di scala, simboli e formulazioni alternative

Diversamente dai vettori momento e momento angolare $\mathbf {p}$ $\mathbf {p}$ ${\mathbf p}$ ed $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ , non esiste ancora una definizione universalmente accettata del vettore di Lenz; molti differenti fattori di scala e simboli sono stati utilizzati nella letteratura scientifica. La definizione più comune è stata fornita sopra , ma un'altra alternativa comune è di dividere il vettore per la costante $m k$ ${\displaystyle mk}$ $mk$ così da ottenere il vettore eccentricità privo di dimensioni

\mathbf {e} ={\frac {1}{mk}}\left(\mathbf {p} \times \mathbf {L} \right)-\mathbf {\hat {r}} ={\frac {m}{k}}\left(\mathbf {v} \times \left(\mathbf {r} \times \mathbf {v} \right)\right)-\mathbf {\hat {r}}

\mathbf {e} ={\frac {1}{mk}}\left(\mathbf {p} \times \mathbf {L} \right)-\mathbf {\hat {r}} ={\frac {m}{k}}\left(\mathbf {v} \times \left(\mathbf {r} \times \mathbf {v} \right)\right)-\mathbf {\hat {r}}

\mathbf {e} ={\frac {1}{mk}}\left(\mathbf {p} \times \mathbf {L} \right)-\mathbf {\hat {r}} ={\frac {m}{k}}\left(\mathbf {v} \times \left(\mathbf {r} \times \mathbf {v} \right)\right)-\mathbf {\hat {r}}

dove $\mathbf {v}$ $\mathbf {v}$ $\mathbf v$ è il vettore velocità. Questo vettore scalato $\mathbf {e}$ $\mathbf {e}$ $\mathbf {e}$ ha la stessa direzione di $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ e modulo equivalente all'eccentricità dell'orbita. Altre versioni scalate possono essere utilizzate con successo, ad es. dividendo $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ per la sola massa $m$ ${\displaystyle m}$ $m$ :

\mathbf {M} =\mathbf {v} \times \mathbf {L} -k\mathbf {\hat {r}}

\mathbf {M} =\mathbf {v} \times \mathbf {L} -k\mathbf {\hat {r}}

\mathbf {M} =\mathbf {v} \times \mathbf {L} -k\mathbf {\hat {r}}

o per $p_{0}$ $p_{0}$ $p_{0}$ :

\mathbf {D} ={\frac {\mathbf {A} }{p_{0}}}={\frac {1}{\sqrt {2m\left|E\right|}}}\left\{\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} \right\}

\mathbf {D} ={\frac {\mathbf {A} }{p_{0}}}={\frac {1}{\sqrt {2m\left|E\right|}}}\left\{\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} \right\}

\mathbf {D} ={\frac {\mathbf {A} }{p_{0}}}={\frac {1}{\sqrt {2m\left|E\right|}}}\left\{\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} \right\}

in modo da ottenere un vettore con le stesse unità del momento angolare $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ . in rari casi, il verso del vettore di Lenz può essere rivoltato, ovvero moltiplicando il vettore per $-1$ ${\displaystyle -1}$ $-1$ . Altri simboli utilizzati per il vettore di Lenz sono $\mathbf {a} ,\mathbf {R} ,\mathbf {F} ,\mathbf {J}$ $\mathbf {a} ,\mathbf {R} ,\mathbf {F} ,\mathbf {J}$ $\mathbf {a} ,\mathbf {R} ,\mathbf {F} ,\mathbf {J}$ e $\mathbf {V}$ $\mathbf {V}$ $\mathbf {V}$ . Tuttavia, la scelta di fattori di scala e simboli per $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ non affligge in alcun modo le sue proprietà.

Figura 4: Il vettore momento angolare

\mathbf {L}

\mathbf {L}

{\mathbf L}

, il vettore di Lenz

\mathbf {A}

\mathbf {A}

\mathbf A

ed il vettore di Hamilton

\mathbf {B}

\mathbf {B}

\mathbf B

, sono mutuamente perpendicolari;

\mathbf {A}

\mathbf {A}

\mathbf A

e

\mathbf {B}

\mathbf {B}

\mathbf B

puntano lungo i due semiassi maggiori e minore, rispettivamente, dell'orbita ellittica.

un vettore costante alternativo è il vettore binormale $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ studiato da William Rowan Hamilton

\mathbf {B} =\mathbf {p} -\left({\frac {mk}{L^{2}r}}\right)\ \left(\mathbf {L} \times \mathbf {r} \right)

\mathbf {B} =\mathbf {p} -\left({\frac {mk}{L^{2}r}}\right)\ \left(\mathbf {L} \times \mathbf {r} \right)

\mathbf {B} =\mathbf {p} -\left({\frac {mk}{L^{2}r}}\right)\ \left(\mathbf {L} \times \mathbf {r} \right)

che è costante e punta lungo il semiasse minore dell'ellisse, il vettore di Lenz $\mathbf {A} =\mathbf {B} \times \mathbf {L}$ $\mathbf {A} =\mathbf {B} \times \mathbf {L}$ $\mathbf {A} =\mathbf {B} \times \mathbf {L}$ è il prodotto vettoriale di $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ ed $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ . Simile al vettore di Lenz esso stesso, il vettore binormale può essere definito con differenti simboli di scala.

I due vettori conservati, $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ e $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ , possono essere combinati per formare un tensore diadico $\mathbf {W}$ $\mathbf {W}$ $\mathbf {W}$ ^[7]

\mathbf {W} =\alpha \mathbf {A} \otimes \mathbf {A} +\beta \,\mathbf {B} \otimes \mathbf {B}

\mathbf {W} =\alpha \mathbf {A} \otimes \mathbf {A} +\beta \,\mathbf {B} \otimes \mathbf {B}

\mathbf {W} =\alpha \mathbf {A} \otimes \mathbf {A} +\beta \,\mathbf {B} \otimes \mathbf {B}

dove $\alpha$ $\alpha$ $\alpha$ e $\beta$ $\beta$ $\beta$ sono arbitrarie costanti di scala e $\otimes$ $\otimes$ $\otimes$ rappresenta il prodotto tensoriale . Scritto in componenti esplicite, questa equazione assume la formula:

W_{ij}=\alpha A_{i}A_{j}+\beta B_{i}B_{j}\,

W_{ij}=\alpha A_{i}A_{j}+\beta B_{i}B_{j}\,

W_{ij}=\alpha A_{i}A_{j}+\beta B_{i}B_{j}\,

Essendo perpendicolari l'uno all'altro, i vettori $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ e $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ possono essere visti come gli assi principali del tensore $\mathbf {W}$ $\mathbf {W}$ $\mathbf {W}$ . $\mathbf {W}$ $\mathbf {W}$ $\mathbf {W}$ è perpendicolare ad $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ :

\mathbf {L} \cdot \mathbf {W} =\alpha \left(\mathbf {L} \cdot \mathbf {A} \right)\mathbf {A} +\beta \left(\mathbf {L} \cdot \mathbf {B} \right)\mathbf {B} =0

\mathbf {L} \cdot \mathbf {W} =\alpha \left(\mathbf {L} \cdot \mathbf {A} \right)\mathbf {A} +\beta \left(\mathbf {L} \cdot \mathbf {B} \right)\mathbf {B} =0

\mathbf {L} \cdot \mathbf {W} =\alpha \left(\mathbf {L} \cdot \mathbf {A} \right)\mathbf {A} +\beta \left(\mathbf {L} \cdot \mathbf {B} \right)\mathbf {B} =0

poiché $\mathbf {A}$ $\mathbf {A}$ $\mathbf A$ e $\mathbf {B}$ $\mathbf {B}$ $\mathbf B$ sono entrambi perpendicolari a $\mathbf {L}$ $\mathbf {L}$ ${\mathbf L}$ , $\mathbf {L} \cdot \mathbf {A} =\mathbf {L} \cdot \mathbf {B} =0$ $\mathbf {L} \cdot \mathbf {A} =\mathbf {L} \cdot \mathbf {B} =0$ $\mathbf {L} \cdot \mathbf {A} =\mathbf {L} \cdot \mathbf {B} =0$ . Con maggiore chiarezza, questa equazione scritta in componenti esplicite diventa:

\left(\mathbf {L} \cdot \mathbf {W} \right)_{j}=\alpha \left(\sum _{i=1}^{3}L_{i}A_{i}\right)A_{j}+\beta \left(\sum _{i=1}^{3}L_{i}B_{i}\right)B_{j}=0

\left(\mathbf {L} \cdot \mathbf {W} \right)_{j}=\alpha \left(\sum _{i=1}^{3}L_{i}A_{i}\right)A_{j}+\beta \left(\sum _{i=1}^{3}L_{i}B_{i}\right)B_{j}=0

\left(\mathbf {L} \cdot \mathbf {W} \right)_{j}=\alpha \left(\sum _{i=1}^{3}L_{i}A_{i}\right)A_{j}+\beta \left(\sum _{i=1}^{3}L_{i}B_{i}\right)B_{j}=0

.

Note

^ ^a ^b ^c ^d ^e ^f ^g H. Goldstein , Classical Mechanics , 2nd edition, Addison Wesley, 1980, pp. 102–105,421–422.
^ VI Arnold , Mathematical Methods of Classical Mechanics, 2nd ed. , New York, Springer-Verlag, 1989, p. 38, ISBN 0-387-96890-3 .
^ ^a ^b W Pauli , Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik , in Zeitschrift für Physik , vol. 36, 1926, pp. 336–363, DOI : 10.1007/BF01450175 .
^ ^a ^b ^c V Fock , Zur Theorie des Wasserstoffatoms , in Zeitschrift für Physik , vol. 98, 1935, pp. 145–154, DOI : 10.1007/BF01336904 .
^ ^a ^b V Bargmann , Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock , in Zeitschrift für Physik , vol. 99, 1936, pp. 576–582, DOI : 10.1007/BF01338811 .
^ ^a ^b WR Hamilton , The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction , in Proceedings of the Royal Irish Academy , vol. 3, 1847, pp. 344-353.
^ ^a ^b ^c ^d ^e DM Fradkin, Existence of the Dynamic Symmetries O ₄ and SU ₃ for All Classical Central Potential Problems , in Progress of Theoretical Physics , vol. 37, 1967, pp. 798–812, DOI : 10.1143/PTP.37.798 .
^ ^a ^b T Yoshida, Two methods of generalisation of the Laplace–Runge–Lenz vector , in European Journal of Physics , vol. 8, 1987, pp. 258–259, DOI :10.1088/0143-0807/8/4/005 .
^ J Hermann , Unknown title , in Giornale de Letterati D'Italia , vol. 2, 1710, pp. 447–467.
J Hermann , Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710 , in Histoire de l'academie royale des sciences (Paris) , vol. 1732, 1710, pp. 519–521.
^ J Bernoulli , Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710 , in Histoire de l'academie royale des sciences (Paris) , vol. 1732, 1710, pp. 521–544.
^ PS Laplace , Traité de mécanique celeste , 1799, Tome I, Premiere Partie, Livre II, pp.165ff.
^ JW Gibbs , Wilson EB, Vector Analysis , New York, Scribners, 1901, p. 135.
^ C Runge ,Vektoranalysis , Leipzig, Hirzel, 1919, Volume I.
^ W Lenz , Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung , in Zeitschrift für Physik , vol. 24, 1924, pp. 197–207, DOI : 10.1007/BF01327245 .
^ NW Evans, Superintegrability in classical mechanics , in Physical Review a , vol. 41, 1990, pp. 5666–5676, DOI : 10.1103/PhysRevA.41.5666 .
^ A Sommerfeld , Atomic Structure and Spectral Lines , London, Methuen, 1923, p. 118.
^ ^a ^b ^c LD Landau , EM Lifshitz , Mechanics , 3rd edition, Pergamon Press, 1976, p. 154, ISBN 0-08-021022-8 , (hardcover) and(softcover).
^ T Curtright, Zachos C, Classical and Quantum Nambu Mechanics , in Physical Review , D68, 2003, p. 085001, DOI : 10.1103/PhysRevD.68.085001 .
^ NW Evans, Group theory of the Smorodinsky–Winternitz system , in Journal of Mathematical Physics , vol. 32, 1991, pp. 3369–3375, DOI : 10.1063/1.529449 .
^ C Zachos, Curtright T, Branes, quantum Nambu brackets, and the hydrogen atom , in Czech Journal of Physics , vol. 54, 2004, pp. 1393–1398, DOI : 10.1007/s10582-004-9807-x .
^ ^a ^b A Einstein , Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie , in Sitzungsberichte der Preussischen Akademie der Wissenschaften , vol. 1915, 1915, pp. 831–839.
^ UJJ Le Verrier , Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète , in Comptes Rendus de l'Academie de Sciences (Paris) , vol. 49, 1859, pp. 379–383.
^ CM Will, General Relativity, an Einstein Century Survey , SW Hawking and W Israel, eds., Cambridge, Cambridge University Press, 1979, Chapter 2.
^ A. Pais , Subtle is the Lord: The Science and the Life of Albert Einstein , Oxford University Press, 1982.
^ NT Roseveare, Mercury's Perihelion from Le Verrier to Einstein , Oxford University Press, 1982.
^ ^a ^b ^c A. Bohm, Quantum Mechanics: Foundations and Applications , 2nd edition, Springer Verlag, 1986, pp. 208–222.
^ PAM Dirac , Principles of Quantum Mechanics, 4th revised edition , Oxford University Press, 1958.
^ E Schrödinger , Quantisierung als Eigenwertproblem , in Annalen der Physik , vol. 384, 1926, pp. 361–376, DOI : 10.1002/andp.19263840404 .
^ ^a ^b M Bander, Itzykson C , Group Theory and the Hydrogen Atom (I) , in Reviews of Modern Physics , vol. 38, 1966, pp. 330–345, DOI : 10.1103/RevModPhys.38.330 .
^ M Bander, Itzykson C, Group Theory and the Hydrogen Atom (II) , in Reviews of Modern Physics , vol. 38, 1966, pp. 346–358, DOI : 10.1103/RevModPhys.38.346 .
^ HH Rogers, Symmetry transformations of the classical Kepler problem , in Journal of Mathematical Physics , vol. 14, 1973, pp. 1125–1129, DOI : 10.1063/1.1666448 .
^ [[ Victor Guillemin |V Guillemin]], Sternberg S, Variations on a Theme by Kepler , American Mathematical Society Colloquium Publications, volume 42, 1990, ISBN 0-8218-1042-1 .
^ M Lakshmanan, Hasegawa H, On the canonical equivalence of the Kepler problem in coordinate and momentum spaces , in Journal of Physics a , vol. 17, 1984, pp. L889–L893, DOI : 10.1088/0305-4470/17/16/006 .
^ PJ Redmond, Generalization of the Runge–Lenz Vector in the Presence of an Electric Field , in Physical Review , vol. 133, 1964, pp. B1352–B1353, DOI : 10.1103/PhysRev.133.B1352 .
^ VA Dulock, McIntosh HV, On the Degeneracy of the Kepler Problem , in Pacific Journal of Mathematics , vol. 19, 1966, pp. 39–55.
^ JM Lévy-Leblond , Conservation Laws for Gauge-Invariant Lagrangians in Classical Mechanics , in American Journal of Physics , vol. 39, 1971, pp. 502–506, DOI : 10.1119/1.1986202 .
^ F Gonzalez-Gascon, Notes on the symmetries of systems of differential equations , in Journal of Mathematical Physics , vol. 18, 1977, pp. 1763–1767, DOI : 10.1063/1.523486 .
^ S Lie ,Vorlesungen über Differentialgleichungen , Leipzig, Teubner, 1891.
^ EL Ince, Ordinary Differential Equations , New York, Dover (1956 reprint), 1926, pp. 93–113.
^ GE Prince, Eliezer CJ, On the Lie symmetries of the classical Kepler problem , in Journal of Physics A: Mathematical and General , vol. 14, 1981, pp. 587–596, DOI : 10.1088/0305-4470/14/3/009 .

Bibliografia

( EN ) John Baez, Mysteries of the gravitational 2-body problem , su math.ucr.edu . URL consultato il 20 giugno 2009 (archiviato dall' url originale il 21 ottobre 2008) .
( EN ) PGL Leach, GP Flessas, Generalisations of the Laplace–Runge–Lenz vector , in J. Nonlinear Math. Phys. , vol. 10, 2003, pp. 340–423, DOI : 10.2991/jnmp.2003.10.3.6 .

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su Vettore di Lenz

Portale Meccanica

Portale Quantistica

[goldstein_1980-1] ^ ^a ^b ^c ^d ^e ^f ^g H. Goldstein , Classical Mechanics , 2nd edition, Addison Wesley, 1980, pp. 102–105,421–422.

[2] VI Arnold , Mathematical Methods of Classical Mechanics, 2nd ed. , New York, Springer-Verlag, 1989, p. 38, ISBN 0-387-96890-3 .

[pauli_1926-3] W Pauli , Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik , in Zeitschrift für Physik , vol. 36, 1926, pp. 336–363, DOI : 10.1007/BF01450175 .

[fock_1935-4] V Fock , Zur Theorie des Wasserstoffatoms , in Zeitschrift für Physik , vol. 98, 1935, pp. 145–154, DOI : 10.1007/BF01336904 .

[bargmann_1936-5] V Bargmann , Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock , in Zeitschrift für Physik , vol. 99, 1936, pp. 576–582, DOI : 10.1007/BF01338811 .

[hamilton_1847_hodograph-6] WR Hamilton , The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction , in Proceedings of the Royal Irish Academy , vol. 3, 1847, pp. 344-353.

[fradkin_1967-7] DM Fradkin, Existence of the Dynamic Symmetries O ₄ and SU ₃ for All Classical Central Potential Problems , in Progress of Theoretical Physics , vol. 37, 1967, pp. 798–812, DOI : 10.1143/PTP.37.798 .

[yoshida_1987-8] T Yoshida, Two methods of generalisation of the Laplace–Runge–Lenz vector , in European Journal of Physics , vol. 8, 1987, pp. 258–259, DOI :10.1088/0143-0807/8/4/005 .

[9] J Hermann , Unknown title , in Giornale de Letterati D'Italia , vol. 2, 1710, pp. 447–467.
J Hermann , Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710 , in Histoire de l'academie royale des sciences (Paris) , vol. 1732, 1710, pp. 519–521.

[10] J Bernoulli , Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710 , in Histoire de l'academie royale des sciences (Paris) , vol. 1732, 1710, pp. 521–544.

[11] PS Laplace , Traité de mécanique celeste , 1799, Tome I, Premiere Partie, Livre II, pp.165ff.

[12] JW Gibbs , Wilson EB, Vector Analysis , New York, Scribners, 1901, p. 135.

[13] C Runge ,Vektoranalysis , Leipzig, Hirzel, 1919, Volume I.

[14] W Lenz , Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung , in Zeitschrift für Physik , vol. 24, 1924, pp. 197–207, DOI : 10.1007/BF01327245 .

[15] NW Evans, Superintegrability in classical mechanics , in Physical Review a , vol. 41, 1990, pp. 5666–5676, DOI : 10.1103/PhysRevA.41.5666 .

[16] A Sommerfeld , Atomic Structure and Spectral Lines , London, Methuen, 1923, p. 118.

[landau_lifshitz_1976-17] LD Landau , EM Lifshitz , Mechanics , 3rd edition, Pergamon Press, 1976, p. 154, ISBN 0-08-021022-8 , (hardcover) and(softcover).

[18] T Curtright, Zachos C, Classical and Quantum Nambu Mechanics , in Physical Review , D68, 2003, p. 085001, DOI : 10.1103/PhysRevD.68.085001 .

[19] NW Evans, Group theory of the Smorodinsky–Winternitz system , in Journal of Mathematical Physics , vol. 32, 1991, pp. 3369–3375, DOI : 10.1063/1.529449 .

[20] C Zachos, Curtright T, Branes, quantum Nambu brackets, and the hydrogen atom , in Czech Journal of Physics , vol. 54, 2004, pp. 1393–1398, DOI : 10.1007/s10582-004-9807-x .

[einstein_1915-21] A Einstein , Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie , in Sitzungsberichte der Preussischen Akademie der Wissenschaften , vol. 1915, 1915, pp. 831–839.

[22] UJJ Le Verrier , Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète , in Comptes Rendus de l'Academie de Sciences (Paris) , vol. 49, 1859, pp. 379–383.

[23] CM Will, General Relativity, an Einstein Century Survey , SW Hawking and W Israel, eds., Cambridge, Cambridge University Press, 1979, Chapter 2.

[24] A. Pais , Subtle is the Lord: The Science and the Life of Albert Einstein , Oxford University Press, 1982.

[25] NT Roseveare, Mercury's Perihelion from Le Verrier to Einstein , Oxford University Press, 1982.

[bohm_1986-26] A. Bohm, Quantum Mechanics: Foundations and Applications , 2nd edition, Springer Verlag, 1986, pp. 208–222.

[27] PAM Dirac , Principles of Quantum Mechanics, 4th revised edition , Oxford University Press, 1958.

[28] E Schrödinger , Quantisierung als Eigenwertproblem , in Annalen der Physik , vol. 384, 1926, pp. 361–376, DOI : 10.1002/andp.19263840404 .

[bander_itzykson_1966-29] M Bander, Itzykson C , Group Theory and the Hydrogen Atom (I) , in Reviews of Modern Physics , vol. 38, 1966, pp. 330–345, DOI : 10.1103/RevModPhys.38.330 .

[30] M Bander, Itzykson C, Group Theory and the Hydrogen Atom (II) , in Reviews of Modern Physics , vol. 38, 1966, pp. 346–358, DOI : 10.1103/RevModPhys.38.346 .

[rogers_1973-31] HH Rogers, Symmetry transformations of the classical Kepler problem , in Journal of Mathematical Physics , vol. 14, 1973, pp. 1125–1129, DOI : 10.1063/1.1666448 .

[32] [[ Victor Guillemin |V Guillemin]], Sternberg S, Variations on a Theme by Kepler , American Mathematical Society Colloquium Publications, volume 42, 1990, ISBN 0-8218-1042-1 .

[33] M Lakshmanan, Hasegawa H, On the canonical equivalence of the Kepler problem in coordinate and momentum spaces , in Journal of Physics a , vol. 17, 1984, pp. L889–L893, DOI : 10.1088/0305-4470/17/16/006 .

[34] PJ Redmond, Generalization of the Runge–Lenz Vector in the Presence of an Electric Field , in Physical Review , vol. 133, 1964, pp. B1352–B1353, DOI : 10.1103/PhysRev.133.B1352 .

[35] VA Dulock, McIntosh HV, On the Degeneracy of the Kepler Problem , in Pacific Journal of Mathematics , vol. 19, 1966, pp. 39–55.

[36] JM Lévy-Leblond , Conservation Laws for Gauge-Invariant Lagrangians in Classical Mechanics , in American Journal of Physics , vol. 39, 1971, pp. 502–506, DOI : 10.1119/1.1986202 .

[37] F Gonzalez-Gascon, Notes on the symmetries of systems of differential equations , in Journal of Mathematical Physics , vol. 18, 1977, pp. 1763–1767, DOI : 10.1063/1.523486 .

[38] S Lie ,Vorlesungen über Differentialgleichungen , Leipzig, Teubner, 1891.

[39] EL Ince, Ordinary Differential Equations , New York, Dover (1956 reprint), 1926, pp. 93–113.

[prince_eliezer_1981-40] GE Prince, Eliezer CJ, On the Lie symmetries of the classical Kepler problem , in Journal of Physics A: Mathematical and General , vol. 14, 1981, pp. 587–596, DOI : 10.1088/0305-4470/14/3/009 .

[1 ]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]