Câmpul vector

Reprezentarea vizuală a unui câmp vector continuu pe plan

În matematică , un câmp vectorial pe un spațiu euclidian este o construcție a calculului vectorial care asociază un vector cu același spațiu la fiecare punct al unei regiuni a unui spațiu euclidian .

Un câmp vector tangent pe o varietate diferențiată este o funcție care asociază fiecărui punct al varietății un vector al tangenței spațiale în acel punct la varietate. Teorema Helmholtz este fundamentală pentru aceste obiecte, întrucât afirmă că cunoașterea divergenței și a rotorului sunt necesare și suficiente pentru cunoașterea câmpului în sine.

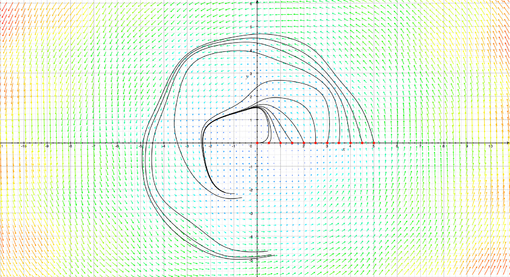
Un câmp vectorial pe plan poate fi reprezentat vizual prin gândirea la o distribuție în plan a vectorilor bidimensionali, astfel încât imaginea vectorială a punctului $X$ ${\ displaystyle x}$ $X$ au originea în $X$ ${\ displaystyle x}$ $X$ în sine (în cele din urmă redimensionată pentru o redare vizuală mai bună ca în figură). În mod similar, câmpurile vectoriale pot fi vizualizate pe suprafețe sau în spațiu tridimensional.

Reprezentarea unui câmp vectorial pe o sferă .

Descriere

Definiție

Având în vedere un întreg deschis și conectat $X$ ${\ displaystyle X}$ $X$ cuprins în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , un câmp vector este o funcție :

F:X\rightarrow \mathbb {R} ^{n}

{\ displaystyle F: X \ rightarrow \ mathbb {R} ^ {n}}

{\ displaystyle F: X \ rightarrow \ mathbb {R} ^ {n}}

care se cere în general să fie continuu sau diferențiat pentru un anumit număr de ori. Ca o funcție, de exemplu, în cazul suprafeței , putem scrie:

{\mathbf {v} }=F(x,y,t)

{\ displaystyle {\ mathbf {v}} = F (x, y, t)}

{\ displaystyle {\ mathbf {v}} = F (x, y, t)}

adică un vector este asociat cu fiecare punct de pe suprafață

în timp ce în cazul spațiului:

{\mathbf {v} }=F(x,y,z,t)

{\ displaystyle {\ mathbf {v}} = F (x, y, z, t)}

{\ displaystyle {\ mathbf {v}} = F (x, y, z, t)}

adică un vector este asociat cu fiecare punct din spațiu

Liniile de curgere

Liniile de curgere care ies din diferite puncte.

Liniile de curgere sunt curbe intuitive care urmează în fiecare punct direcțiile identificate de câmpul vector cu viteza dată de amplitudinea vectorilor câmpului. Interpretând câmpul vector ca un câmp de viteză al unui fluid , aceste linii reprezintă traiectoriile fiecărei particule individuale. În mod formal, o linie de curgere care trece printr-un punct $X$ ${\ displaystyle x}$ $X$ este o curbă diferențiată :

\phi :(-R,R)\to X

{\ displaystyle \ phi: (- R, R) \ to X}

{\ displaystyle \ phi: (- R, R) \ to X}

definit pentru unii $R.$ ${\ displaystyle R}$ $R.$ pozitiv, astfel încât

\phi (0)=x

{\ displaystyle \ phi (0) = x}

{\ displaystyle \ phi (0) = x}

Și

\phi '(t)=F(\phi (t))

{\ displaystyle \ phi '(t) = F (\ phi (t))}

{\ displaystyle \ phi '(t) = F (\ phi (t))}

pentru fiecare

t

{\ displaystyle t}

t

.

Dacă câmpul este suficient de „regulat” (de exemplu, dacă $F.$ ${\ displaystyle F}$ $F.$ este diferențiat sau cel puțin Lipschitzian ), exact o linie de curgere trece prin fiecare punct. Acest lucru se datorează faptului că o linie de curgere este soluția unei probleme Cauchy , a cărei existență și unicitate sunt garantate de teorema existenței și unicității pentru o problemă Cauchy .

Fluxul de fază asociat cu un câmp vector

O linie de curgere este definită pe un interval deschis $(-R,R)$ ${\ displaystyle (-R, R)}$ ${\ displaystyle (-R, R)}$ , dar nu este neapărat definit pe întreaga linie reală . Într-un câmp vector astfel încât toate liniile de flux să fie definite pe întreaga linie reală, este posibil să se definească o aplicație

\Phi :\mathbb {R} \times X\to X

{\ displaystyle \ Phi: \ mathbb {R} \ times X \ to X}

{\ displaystyle \ Phi: \ mathbb {R} \ times X \ to X}

care se asociază cu un cuplu $(t,x)$ ${\ displaystyle (t, x)}$ ${\ displaystyle (t, x)}$ - dat de un timp și un punct în spațiul de fază - punctul de sosire care se obține urmărind linia de curgere de la care începe $X$ ${\ displaystyle x}$ $X$ pentru o vreme $t$ ${\ displaystyle t}$ $t$ începând de la punct $X$ ${\ displaystyle x}$ $X$ . Această aplicație este fluxul asociat câmpului vector și este obișnuit să scrieți $\Phi _{t}(x)$ ${\ displaystyle \ Phi _ {t} (x)}$ ${\ displaystyle \ Phi _ {t} (x)}$ pentru a indica imaginea cuplului $(t,x)$ ${\ displaystyle (t, x)}$ ${\ displaystyle (t, x)}$ .

Formal fluxul asociat cu câmpul vector $F.$ ${\ displaystyle F}$ $F.$ este identificat printr-o familie de aplicații

\{\Phi _{t}:X\to X\,|\,t\in \mathbb {R} \}

{\ displaystyle \ {\ Phi _ {t}: X \ to X \, | \, t \ in \ mathbb {R} \}}

{\ displaystyle \ {\ Phi _ {t}: X \ to X \, | \, t \ in \ mathbb {R} \}}

care verifică condițiile:

{\begin{cases}\Phi _{0}(x)=x\\\left.{\frac {d}{dt}}\Phi _{t}(x)\right|_{t=t_{0}}=F(\Phi _{t_{0}}(x))\end{cases}}

{\ displaystyle {\ begin {cases} \ Phi _ {0} (x) = x \\\ left. {\ frac {d} {dt}} \ Phi _ {t} (x) \ right | _ {t = t_ {0}} = F (\ Phi _ {t_ {0}} (x)) \ end {cases}}}

{\ displaystyle {\ begin {cases} \ Phi _ {0} (x) = x \\\ left. {\ frac {d} {dt}} \ Phi _ {t} (x) \ right | _ {t = t_ {0}} = F (\ Phi _ {t_ {0}} (x)) \ end {cases}}}

pentru fiecare $X$ ${\ displaystyle x}$ $X$ și pentru orice moment $t_{0}$ ${\ displaystyle t_ {0}}$ $t_ {0}$ .

Fluxul este un „grup cu un singur parametru”: este un grup deoarece îndeplinește următoarele proprietăți

$\Phi _{0}={\mbox{Id}}_{X}$ ${\ displaystyle \ Phi _ {0} = {\ mbox {Id}} _ {X}}$ ${\ displaystyle \ Phi _ {0} = {\ mbox {Id}} _ {X}}$
$\Phi _{s+t}=\Phi _{s}\circ \Phi _{t}$ ${\ displaystyle \ Phi _ {s + t} = \ Phi _ {s} \ circ \ Phi _ {t}}$ ${\ displaystyle \ Phi _ {s + t} = \ Phi _ {s} \ circ \ Phi _ {t}}$

și definește o acțiune de $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb R$ pe $X$ ${\ displaystyle X}$ $X$ . Proprietățile grupului ne spun în mod informal că evoluția spațiului indusă de flux pentru un timp corespunde lăsării totul așa cum este și că evoluția pentru un timp $s+t$ ${\ displaystyle s + t}$ ${\ displaystyle s + t}$ este echivalent cu aplicarea succesivă a două evoluții pentru timpuri $s$ ${\ displaystyle s}$ $s$ Și $t$ ${\ displaystyle t}$ $t$ .

Puncte critice

Liniile de curgere și punctele critice pentru ecuația pendulului în spațiul de fază

Definiție

Un punct critic sau punct singular pentru un câmp vector este un punct în care câmpul dispare sau în care nu este definit deoarece tinde spre infinit (similar cu ceea ce se întâmplă pentru poli ). În general, se presupune că câmpul este suficient de regulat, astfel încât punctele critice să fie izolate .

Punctele critice își datorează numele rolului „special” pe care îl joacă în câmpul vectorial. În vecinătatea oricărui punct non- critic, structura topologică a câmpului vector este întotdeauna aceeași: câmpul restricționat la un mic vecinătate al punctului este difeomorf la un câmp constant (care asociază același vector non-zero la fiecare punct ), ale căror linii sunt, prin urmare, linii paralele, așa cum este stabilit de teorema cutiei de flux . Punctele critice, pe de altă parte, au un istoric de caz mult mai bogat.

Topologie

Posibilele structuri topologice ale câmpului într-un vecinătate al punctului critic izolat pot fi clasificate prin asocierea unui număr întreg numit index punctelor critice.

Tipul și numărul total de puncte critice ale unui câmp vector sunt, de asemenea, legate de structura topologică globală a domeniului pe care este definit câmpul. Această legătură este stabilită de teorema Poincaré-Hopf care afirmă că, dacă câmpul vector este definit pe o varietate compactă diferențiată, atunci suma indicilor punctelor sale critice este egală cu caracteristica Euler a varietății.

Soiuri combabile

Un colector diferențial poate fi pieptănat dacă admite un câmp vectorial (suficient de regulat) care nu este niciodată nul. Prin teorema lui Poincaré-Hopf menționată mai sus, o varietate compactă compactă trebuie să aibă caracteristica Euler zero. Din acest motiv, sfera nu poate fi pieptănată: această afirmație este teorema sferei păroase .

Pe de altă parte, torul și sticla Klein sunt suprafețe cu caracteristica zero Euler și pot fi pieptănate.

Aplicații

Instrument care arată configurația unui câmp magnetic .

Câmpurile vectoriale sunt întâlnite atât în matematică pură, cât și în matematică aplicată:

În fizică sunt folosite pentru a modela mărimi vectoriale distribuite cu continuitate în spațiu, mărimi caracterizate printr-o intensitate și o direcție, de exemplu deplasarea, viteza și accelerația unui fluid, câmpuri de forțe, ca în cazul unui gravitațional , electric sau magnetic , vânturi în meteorologie etc.

În analiza și studiul sistemelor dinamice , câmpurile vectoriale sunt strâns legate de ecuații diferențiale .

În topologia diferențială , studiem legăturile dintre proprietățile câmpurilor vectoriale continue pe o varietate diferențiată și structura topologică a varietății. Un exemplu este teorema bilei păroase care afirmă că pe o sferă (și pe orice suprafață diferită de o sferă) nu este posibil să se definească un câmp vector continuu și niciodată nul.

Exemple

Câmp vector gradient

Același subiect în detaliu: Gradient .

Având o funcție diferențiată pe $X\subset \mathbb {R} ^{n}$ ${\ displaystyle X \ subset \ mathbb {R} ^ {n}}$ $X \ subset \ mathbb R ^ n$

f:X\rightarrow \mathbb {R}

{\ displaystyle f: X \ rightarrow \ mathbb {R}}

{\ displaystyle f: X \ rightarrow \ mathbb {R}}

câmpul de gradient al $f$ ${\ displaystyle f}$ $f$ este câmpul vectorial care se asociază fiecăruia $X$ ${\ displaystyle x}$ ${\ displaystyle x}$ în $X$ ${\ displaystyle X}$ $X$ vectorul

F(x):=\nabla f(x)

{\ displaystyle F (x): = \ nabla f (x)}

{\ displaystyle F (x): = \ nabla f (x)}

dat de gradientul de $f$ ${\ displaystyle f}$ $f$ în $X$ ${\ displaystyle x}$ $X$ .

Un câmp de gradient este conservator , adică rotorul este zero peste tot.

Liniile de flux ale unui câmp de gradient asociat cu o funcție scalară $f$ ${\ displaystyle f}$ $f$ sunt pretutindeni ortogonali față de suprafețele de nivel ale $f$ ${\ displaystyle f}$ $f$ , adică hipersuprafețelor date de ecuația cartesiană $f(x)=c$ ${\ displaystyle f (x) = c}$ $f (x) = c$ dupa cum $c$ ${\ displaystyle c}$ $c$ în $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {R}}$ .

Câmp vectorial hamiltonian

Același subiect în detaliu: câmpul vector hamiltonian .

Având o funcție diferențiată pe un open $X$ ${\ displaystyle X}$ $X$ a planului cartezian $\mathbb {R} ^{2}$ ${\ displaystyle \ mathbb {R} ^ {2}}$ $\ mathbb {R} ^ {2}$ :

H:X\rightarrow \mathbb {R} ^{2}

{\ displaystyle H: X \ rightarrow \ mathbb {R} ^ {2}}

{\ displaystyle H: X \ rightarrow \ mathbb {R} ^ {2}}

câmpul hamiltonian al $H.$ ${\ displaystyle H}$ $H.$ este câmpul vector care se asociază unui punct $(x,y)$ ${\ displaystyle (x, y)}$ $(X y)$ în $X$ ${\ displaystyle X}$ $X$ vectorul

F(x,y)=(H_{y}(x,y),-H_{x}(x,y))

{\ displaystyle F (x, y) = (H_ {y} (x, y), - H_ {x} (x, y))}

{\ displaystyle F (x, y) = (H_ {y} (x, y), - H_ {x} (x, y))}

unde este $H_{x}$ ${\ displaystyle H_ {x}}$ ${\ displaystyle H_ {x}}$ Și $H_{y}$ ${\ displaystyle H_ {y}}$ ${\ displaystyle H_ {y}}$ denotați derivatele parțiale ale $H.$ ${\ displaystyle H}$ $H.$ .

Funcția scalară $H.$ ${\ displaystyle H}$ $H.$ care generează câmpul hamiltonian se numește hamiltonian .

Bibliografie

( EN ) JH Hubbard și BB Hubbard, calcul vectorial, algebră liniară și forme diferențiale. O abordare unificată , Upper Saddle River, NJ, Prentice Hall, 1999, ISBN 0-13-657446-7 .
( EN ) Frank Warner, Fundamentele diferitelor varietăți și grupurile Lie , New York-Berlin, Springer-Verlag, 1983 [1971] , ISBN 0-387-90894-3 .
( EN ) William Boothby, O introducere la varietăți diferențiate și geometria Riemanniană , Matematică pură și aplicată, volumul 120, al doilea, Orlando, FL, Academic Press, 1986, ISBN 0-12-116053-X .
( EN ) Galbis, Antonio & Maestre, Manuel, Vector Analysis Versus Vector Calculus , Springer, 2012, p. 12, ISBN 978-1-4614-2199-3 .
(EN) You, W. Loring, Vector fields , în An Introduction to Manifolds, Springer, 2010, p. 149, ISBN 978-1-4419-7399-3 .
( EN ) Dawber, PG, Vectors and Vector Operators , CRC Press, 1987, p. 29, ISBN 978-0-85274-585-4 .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere de câmp vector

linkuri externe

( EN ) Eric W. Weisstein, câmp Vector , în MathWorld , Wolfram Research.
( EN ) Câmp vectorial , în PlanetMath .
( EN ) Paul Falstad, aplicație Java 2D Vector Field Simulation pentru vizualizarea câmpurilor vector 2D
( EN ) Paul Falstad, aplicație Java de simulare a câmpului 3D 3D pentru vizualizarea câmpurilor vectoriale 3D

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică