Funcția densității probabilității

Funcția densității probabilității unei variabile aleatorii cu distribuție uniformă .

În matematică , o funcție de densitate de probabilitate (PDF engleză sau funcție de densitate de probabilitate) este analogul funcției de probabilitate a unei variabile aleatorii în cazul în care variabila aleatoare $X$ ${\ displaystyle X}$ $X$ este continuu , adică setul de valori posibile pe care le are puterea continuumului . Descrie „densitatea” probabilității în fiecare punct din spațiul eșantion .

Definiție

Funcția densității probabilității unei variabile aleatorii $X$ ${\ displaystyle X}$ $X$ este o aplicație $p_{X}(x)$ ${\ displaystyle p_ {X} (x)}$ $p_ {X} (x)$ integrabil negativ conform lui Lebesgue și real al unei variabile reale astfel încât probabilitatea mulțimii A este dată de

P(X\in A)=\int _{A}p_{X}(x)\,\mathrm {d} x

{\ displaystyle P (X \ în A) = \ int _ {A} p_ {X} (x) \, \ mathrm {d} x}

{\ displaystyle P (X \ în A) = \ int _ {A} p_ {X} (x) \, \ mathrm {d} x}

pentru toate subseturile A din spațiul eșantion . Intuitiv, dacă o distribuție de probabilitate are densitate $p_{X}(x)$ ${\ displaystyle p_ {X} (x)}$ $p_ {X} (x)$ , apoi intervalul $[x,x+\mathrm {d} x]$ ${\ displaystyle [x, x + \ mathrm {d} x]}$ ${\ displaystyle [x, x + \ mathrm {d} x]}$ are cote $p_{X}(x)\,\mathrm {d} x$ ${\ displaystyle p_ {X} (x) \, \ mathrm {d} x}$ ${\ displaystyle p_ {X} (x) \, \ mathrm {d} x}$ . Din aceasta rezultă că funcția $p_{X}(x)$ ${\ displaystyle p_ {X} (x)}$ $p_ {X} (x)$ este o aplicație definită ca

p_{X}({\bar {x}}):{\bar {x}}\mapsto \lim _{\mathrm {d} x\to 0}{\frac {P(x<{\bar {x}}<x+\mathrm {d} x)}{\mathrm {d} x}}

{\ displaystyle p_ {X} ({\ bar {x}}): {\ bar {x}} \ mapsto \ lim _ {\ mathrm {d} x \ to 0} {\ frac {P (x <{\ bara {x}} <x + \ mathrm {d} x)} {\ mathrm {d} x}}}

{\ displaystyle p_ {X} ({\ bar {x}}): {\ bar {x}} \ mapsto \ lim _ {\ mathrm {d} x \ to 0} {\ frac {P (x <{\ bara {x}} <x + \ mathrm {d} x)} {\ mathrm {d} x}}}

Asumând $x\equiv {\bar {x}}$ ${\ displaystyle x \ equiv {\ bar {x}}}$ $x \ equiv {\ bar {x}}$ , aceasta corespunde limitei probabilității ca ${\bar {x}}$ ${\ displaystyle {\ bar {x}}}$ ${\ bar {x}}$ este în raza de acțiune $[x,x+\mathrm {d} x]$ ${\ displaystyle [x, x + \ mathrm {d} x]}$ ${\ displaystyle [x, x + \ mathrm {d} x]}$ pentru $\mathrm {d} x$ ${\ displaystyle \ mathrm {d} x}$ ${\ mathrm {d}} x$ care tinde spre zero. De aici și numele funcției „densitate”, deoarece reprezintă raportul dintre o probabilitate și o amplitudine.

Pentru condiția de normalizare, integralul pe întregul spațiu al $p_{X}(x)$ ${\ displaystyle p_ {X} (x)}$ $p_ {X} (x)$ trebuie să fie 1. În consecință, fiecare funcție non-negativă, integrabilă conform lui Lebesgue, cu integral pe tot spațiul egal cu 1, este funcția densității probabilității unei distribuții de probabilitate bine definite. O variabilă aleatorie care are densitate se numește „ variabilă aleatorie continuă ”.

Pentru variabilele aleatorii multivariate (sau vectoriale) tratamentul formal este absolut identic: $(X_{1},\ldots ,X_{n})$ ${\ displaystyle (X_ {1}, \ ldots, X_ {n})}$ $(X_ {1}, \ ldots, X_ {n})$ se spune că este absolut continuu dacă există o funcție cu valoare reală definită în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , numită densitate articulară , astfel încât pentru fiecare subset A al spațiului eșantion

P(X\in A)=\int _{A}p_{X_{1},\ldots ,X_{n}}(x_{1},\ldots ,x_{n})\,\mathrm {d} x_{1}\ldots \mathrm {d} x_{n}

{\ displaystyle P (X \ in A) = \ int _ {A} p_ {X_ {1}, \ ldots, X_ {n}} (x_ {1}, \ ldots, x_ {n}) \, \ mathrm {d} x_ {1} \ ldots \ mathrm {d} x_ {n}}

{\ displaystyle P (X \ in A) = \ int _ {A} p_ {X_ {1}, \ ldots, X_ {n}} (x_ {1}, \ ldots, x_ {n}) \, \ mathrm {d} x_ {1} \ ldots \ mathrm {d} x_ {n}}

Păstrează toate proprietățile unei densități scalare: este o funcție non-negativă cu o unitate integrală pe tot spațiul. O proprietate importantă este că dacă $(X_{1},\ldots ,X_{n})$ ${\ displaystyle (X_ {1}, \ ldots, X_ {n})}$ $(X_ {1}, \ ldots, X_ {n})$ este absolut continuu, apoi fiecare dintre componentele sale este continuă; invers, pe de altă parte, nu este valid. Densitatea unei componente, numită densitate marginală , se obține cu un raționament analog teoremei probabilității absolute , adică prin fixarea setului de valori ale cărui probabilități urmează să fie determinate și lăsând toate celelalte componente libere să varieze. De fapt (în cazul bivariatului pentru simplitate) evenimentul $(X\in A)$ ${\ displaystyle (X \ în A)}$ $(X \ în A)$ este evenimentul $(X\in A,Y\in \mathbb {R} )$ ${\ displaystyle (X \ în A, Y \ în \ mathbb {R})}$ $(X \ în A, Y \ în \ mathbb {R})$ , asa de

P(X\in A)=\int _{A\times \mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} x\,\mathrm {d} y=\int _{A}\left(\int _{\mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} y\right)\mathrm {d} x

{\ displaystyle P (X \ in A) = \ int _ {A \ times \ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} x \, \ mathrm {d} y = \ int _ {A} \ left (\ int _ {\ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} y \ right) \ mathrm {d} x}

{\ displaystyle P (X \ in A) = \ int _ {A \ times \ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} x \, \ mathrm {d} y = \ int _ {A} \ left (\ int _ {\ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} y \ right) \ mathrm {d} x}

folosind teorema lui Fubini . Densitatea marginală a $X$ ${\ displaystyle X}$ $X$ este deci dat de

p_{X}(x)=\int _{\mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} y

{\ displaystyle p_ {X} (x) = \ int _ {\ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} y}

{\ displaystyle p_ {X} (x) = \ int _ {\ mathbb {R}} p_ {X, Y} (x, y) \, \ mathrm {d} y}

.

Exemple

Exemplu degaussian

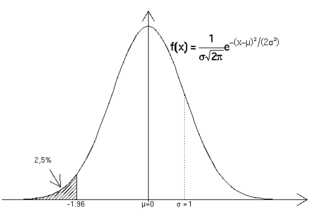
Funcția de densitate avariabilei aleatoare normale cu media 0 și varianța 1 (numită normală standard ), dintre care în dreapta este graficul și expresia analitică a densității corespunzătoare în cazul generic (medie $\mu$ ${\ displaystyle \ mu}$ $\ mu$ și varianță $\sigma ^{2}$ ${\ displaystyle \ sigma ^ {2}}$ $\ sigma ^ {2}$ ).

Un alt exemplu poate fi dat de densitatea de probabilitate uniformă pe un segment (0,1). Putem verifica imediat că este densitatea probabilității făcând integralul între (0,1).

Elemente conexe

linkuri externe

( RO ) IUPAC Gold Book, „densitatea probabilității” , pe goldbook.iupac.org .

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică