Distribuție exponențială

Distribuție exponențială ${\mathcal {E}}(\lambda )$ ${\ displaystyle {\ mathcal {E}} (\ lambda)}$ ${\ mathcal {E}} (\ lambda)$
Funcția densității probabilității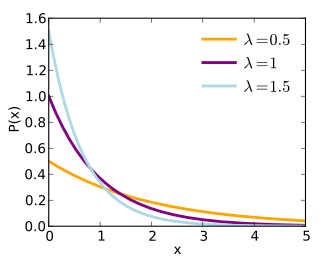
Funcția de distribuție
Parametrii	$\lambda >0\$ ${\ displaystyle \ lambda> 0 \}$ $\ lambda> 0 \$
A sustine	$\mathbb {R} ^{+}$ ${\ displaystyle \ mathbb {R} ^ {+}}$ $\ mathbb {R} ^ {+}$
Funcția de densitate	$\lambda e^{-\lambda x}\$ ${\ displaystyle \ lambda și ^ {- \ lambda x} \}$ $\ lambda și ^ {{- \ lambda x}} \$
Funcția de distribuție	$1-e^{-\lambda x}\$ ${\ displaystyle 1-e ^ {- \ lambda x} \}$ $1-e ^ {{- \ lambda x}} \$
Valorea estimata	${\frac {1}{\lambda }}\$ ${\ displaystyle {\ frac {1} {\ lambda}} \}$ ${\ frac {1} {\ lambda}} \$
Median	${\frac {\log(2)}{\lambda }}$ ${\ displaystyle {\ frac {\ log (2)} {\ lambda}}}$ ${\ frac {\ log (2)} {\ lambda}}$
Modă	$0\$ ${\ displaystyle 0 \}$ $0 \$
Varianța	${\frac {1}{\lambda ^{2}}}$ ${\ displaystyle {\ frac {1} {\ lambda ^ {2}}}}$ ${\ frac {1} {\ lambda ^ {2}}}$
Indicele de asimetrie	$2\$ ${\ displaystyle 2 \}$ $2 \$
Curios	$6\$ ${\ displaystyle 6 \}$ $6 \$
Entropie	$1-\log(\lambda )\$ ${\ displaystyle 1- \ log (\ lambda) \}$ $1- \ log (\ lambda) \$
Funcție generatoare de momente	$\left(1-{\frac {t}{\lambda }}\right)^{-1}$ ${\ displaystyle \ left (1 - {\ frac {t} {\ lambda}} \ right) ^ {- 1}}$ $\ left (1 - {\ frac {t} {\ lambda}} \ right) ^ {{- 1}}$
Funcția caracteristică	$\left(1-{\frac {it}{\lambda }}\right)^{-1}$ ${\ displaystyle \ left (1 - {\ frac {it} {\ lambda}} \ right) ^ {- 1}}$ $\ left (1 - {\ frac {it} {\ lambda}} \ right) ^ {{- 1}}$
Manual

În teoria probabilității, distribuția exponențială este o distribuție continuă a probabilității care descrie „durata de viață” a unui fenomen care nu îmbătrânește (adică distribuția exponențială este lipsită de memorie ). Un exemplu este durata de viață a unei particule radioactive înainte de descompunere sau durata unei cereri pentru un serviciu; de aceea este legat de timpul de așteptare al primului succes, în fenomene aleatorii cu distribuție geometrică.

Distribuția exponențială (sau Laplace) poate fi, de asemenea, dedusă ca distribuția de probabilitate a unei variabile aleatorii definită ca suma pătratelor a două variabile aleatoare normale standardizate (adică cu valoarea zero așteptată și varianța unității); prin urmare, este, de asemenea, atribuibil în mod trivial unui anumit caz de distribuție chi-pătrat, acesta din urmă fiind distribuția probabilității variabilei aleatorii construită ca suma pătratelor a n variabile aleatoare normale și standardizate aleatorii.

Definiție

Distribuția exponențială ${\mathcal {E}}(\lambda )$ ${\ displaystyle {\ mathcal {E}} (\ lambda)}$ ${\ mathcal {E}} (\ lambda)$ , cu parametru $\lambda >0$ ${\ displaystyle \ lambda> 0}$ $\ lambda> 0$ , are funcția de densitate a probabilității :

f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}

{\ displaystyle f (x; \ lambda) = {\ begin {cases} \ lambda e ^ {- \ lambda x} & x \ geq 0, \\ 0 & x <0. \ end {cases}}}

{\ displaystyle f (x; \ lambda) = {\ begin {cases} \ lambda e ^ {- \ lambda x} & x \ geq 0, \\ 0 & x <0. \ end {cases}}}

Proprietate

Parametrul $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ trebuie să fie pozitiv pentru ca integrala funcției de densitate pe reali să fie $1.$ ${\ displaystyle 1.}$ ${\ displaystyle 1.}$

Lipsa memoriei

O variabilă aleatorie $X$ ${\ displaystyle X}$ $X$ cu distribuție exponențială a parametrului $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ are o funcție de distribuție

F(x)=P(X\leqslant x)=1-e^{-\lambda x}.

{\ displaystyle F (x) = P (X \ leqslant x) = 1-e ^ {- \ lambda x}.}

{\ displaystyle F (x) = P (X \ leqslant x) = 1-e ^ {- \ lambda x}.}

În special formula $P(X>x)=e^{-\lambda x}$ ${\ displaystyle P (X> x) = e ^ {- \ lambda x}}$ $P (X> x) = e ^ {{- \ lambda x}}$ implică lipsa memoriei :

P(X>a+b|X>a)={\frac {P(X>a+b)}{P(X>a)}}=P(X>b).

{\ displaystyle P (X> a + b | X> a) = {\ frac {P (X> a + b)} {P (X> a)}} = P (X> b).}

{\ displaystyle P (X> a + b | X> a) = {\ frac {P (X> a + b)} {P (X> a)}} = P (X> b).}

În schimb, dacă o distribuție continuă a probabilității asupra numerelor reale pozitive este lipsită de memorie, adică se respectă ${P(X>a+b)=P(X>a)P(X>b)}$ ${\ displaystyle {P (X> a + b) = P (X> a) P (X> b)}}$ ${P (X> a + b) = P (X> a) P (X> b)}$ pentru fiecare alegere de $la$ ${\ displaystyle a}$ $la$ și de $b,$ ${\ displaystyle b,}$ ${\ displaystyle b,}$ atunci relația este valabilă $P(X>x)=P(X>1)^{x}$ ${\ displaystyle P (X> x) = P (X> 1) ^ {x}}$ $P (X> x) = P (X> 1) ^ {x}$ pentru fiecare $X$ ${\ displaystyle x}$ $X$ pozitiv rațional sau chiar, grație continuității funcției de distribuție, pentru fiecare $X$ ${\ displaystyle x}$ $X$ real pozitiv; mai ales luând $\lambda =-\log P(X>1)$ ${\ displaystyle \ lambda = - \ log P (X> 1)}$ $\ lambda = - \ log P (X> 1)$ este situat chiar

F(x)=1-P(X>x)=1-e^{-\lambda x}.

{\ displaystyle F (x) = 1-P (X> x) = 1-e ^ {- \ lambda x}.}

{\ displaystyle F (x) = 1-P (X> x) = 1-e ^ {- \ lambda x}.}

Pe de altă parte, printre distribuțiile de probabilitate discrete , fiecare distribuție fără memorie este o distribuție geometrică .

Caracteristici

O variabilă aleatorie cu distribuție exponențială a parametrilor $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ are

valorea estimata $E[X]=1/\lambda$ ${\ displaystyle E [X] = 1 / \ lambda}$ $E [X] = 1 / \ lambda$ ,
varianță ${\text{Var}}(X)=1/\lambda ^{2}$ ${\ displaystyle {\ text {Var}} (X) = 1 / \ lambda ^ {2}}$ ${\ text {Var}} (X) = 1 / \ lambda ^ {2}$ ,
funcție caracteristică $\phi _{X}(t)=\left(1-{\frac {it}{\lambda }}\right)^{-1}$ ${\ displaystyle \ phi _ {X} (t) = \ left (1 - {\ frac {it} {\ lambda}} \ right) ^ {- 1}}$ $\ phi _ {X} (t) = \ left (1 - {\ frac {it} {\ lambda}} \ right) ^ {{- 1}}$
funcție generatoare de moment $g_{X}(t)=\left(1-{\frac {t}{\lambda }}\right)^{-1}$ ${\ displaystyle g_ {X} (t) = \ left (1 - {\ frac {t} {\ lambda}} \ right) ^ {- 1}}$ $g_ {X} (t) = \ left (1 - {\ frac {t} {\ lambda}} \ right) ^ {{- 1}}$
indici de asimetrie și curtoză $\gamma _{1}=2$ ${\ displaystyle \ gamma _ {1} = 2}$ $\ gamma _ {1} = 2$ Și $\gamma _{2}=6$ ${\ displaystyle \ gamma _ {2} = 6}$ $\ gamma _ {2} = 6$ .
momente centrale generice $\mu _{n}={\frac {1}{\lambda ^{n}}}!n={\lambda }^{-n}n!\sum _{k=0}^{n}(-1)^{k}/k!={\frac {\Gamma (n+1,-1)}{e\lambda ^{n}}}$ ${\ displaystyle \ mu _ {n} = {\ frac {1} {\ lambda ^ {n}}}! n = {\ lambda} ^ {- n} n! \ sum _ {k = 0} ^ {n } (- 1) ^ {k} / k! = {\ Frac {\ Gamma (n + 1, -1)} {e \ lambda ^ {n}}}}$ ${\ displaystyle \ mu _ {n} = {\ frac {1} {\ lambda ^ {n}}}! n = {\ lambda} ^ {- n} n! \ sum _ {k = 0} ^ {n } (- 1) ^ {k} / k! = {\ Frac {\ Gamma (n + 1, -1)} {e \ lambda ^ {n}}}}$ unde este $! n$ ${\ displaystyle! n}$ $! n$ este factorul secundar al $n$ ${\ displaystyle n}$ $n$ .

Cuantilele sale pot fi obținute prin inversarea funcției de distribuție:

\alpha =F(q_{\alpha })=1-e^{-\lambda q_{\alpha }}

{\ displaystyle \ alpha = F (q _ {\ alpha}) = 1-e ^ {- \ lambda q _ {\ alpha}}}

\ alpha = F (q _ {\ alpha}) = 1-e ^ {{- \ lambda q _ {\ alpha}}}

q_{\alpha }=F^{-1}(\alpha )={\frac {1}{\lambda }}\log {\frac {1}{1-\alpha }}

{\ displaystyle q _ {\ alpha} = F ^ {- 1} (\ alpha) = {\ frac {1} {\ lambda}} \ log {\ frac {1} {1- \ alpha}}}

q _ {\ alpha} = F ^ {{- 1}} (\ alpha) = {\ frac {1} {\ lambda}} \ log {\ frac {1} {1- \ alpha}}

;

în special quartile sale (și mediana ) sunt

q_{1/4}={\frac {1}{\lambda }}\log {\frac {4}{3}}

{\ displaystyle q_ {1/4} = {\ frac {1} {\ lambda}} \ log {\ frac {4} {3}}}

q _ {{1/4}} = {\ frac {1} {\ lambda}} \ log {\ frac {4} {3}}

,

q_{1/2}={\frac {1}{\lambda }}\log 2

{\ displaystyle q_ {1/2} = {\ frac {1} {\ lambda}} \ log 2}

q _ {{1/2}} = {\ frac {1} {\ lambda}} \ log 2

,

q_{3/4}={\frac {1}{\lambda }}\log 4

{\ displaystyle q_ {3/4} = {\ frac {1} {\ lambda}} \ log 4}

q _ {{3/4}} = {\ frac {1} {\ lambda}} \ log 4

.

Distribuții

Minimul $Y=\min\{X_{1},\dots ,X_{n}\}$ ${\ displaystyle Y = \ min \ {X_ {1}, \ dots, X_ {n} \}}$ $Y = \ min \ {X_ {1}, \ dots, X_ {n} \}$ între $n$ ${\ displaystyle n}$ $n$ variabile aleatorii independente cu distribuții exponențiale ale parametrilor $\lambda _{1},\dots ,\lambda _{n}$ ${\ displaystyle \ lambda _ {1}, \ dots, \ lambda _ {n}}$ $\ lambda _ {1}, \ dots, \ lambda _ {n}$ este încă o variabilă aleatorie cu distribuție exponențială a parametrilor $\lambda =\lambda _{1}+\dots +\lambda _{n}$ ${\ displaystyle \ lambda = \ lambda _ {1} + \ dots + \ lambda _ {n}}$ $\ lambda = \ lambda _ {1} + \ dots + \ lambda _ {n}$ .

Paralela distribuției exponențiale, ca distribuție fără memorie, între distribuțiile discrete de probabilitate este distribuția geometrică . În special, dacă $X$ ${\ displaystyle X}$ $X$ urmează distribuția exponențială ${\mathcal {E}}(\lambda )$ ${\ displaystyle {\ mathcal {E}} (\ lambda)}$ ${\ mathcal {E}} (\ lambda)$ apoi pentru fiecare $\theta >0$ ${\ displaystyle \ theta> 0}$ $\ theta> 0$ variabila aleatorie $Y_{\theta }=[\theta X]$ ${\ displaystyle Y _ {\ theta} = [\ theta X]}$ $Y _ {\ theta} = [\ theta X]$ ( partea întreagă ) urmează distribuția geometrică ${\mathcal {G}}(e^{-\lambda /\theta })$ ${\ displaystyle {\ mathcal {G}} (e ^ {- \ lambda / \ theta})}$ ${\ mathcal {G}} (e ^ {{- \ lambda / \ theta}})$ :

P(Y=n)=P(n\leqslant \theta X<n+1)=F_{X}\left({\frac {n+1}{\theta }}\right)-F_{X}\left({\frac {n}{\theta }}\right)=\left(1-e^{-\lambda /\theta }\right)\left(e^{-\lambda /\theta }\right)^{n}.

{\ displaystyle P (Y = n) = P (n \ leqslant \ theta X <n + 1) = F_ {X} \ left ({\ frac {n + 1} {\ theta}} \ right) -F_ { X} \ left ({\ frac {n} {\ theta}} \ right) = \ left (1-e ^ {- \ lambda / \ theta} \ right) \ left (e ^ {- \ lambda / \ theta } \ dreapta) ^ {n}.}

{\ displaystyle P (Y = n) = P (n \ leqslant \ theta X <n + 1) = F_ {X} \ left ({\ frac {n + 1} {\ theta}} \ right) -F_ { X} \ left ({\ frac {n} {\ theta}} \ right) = \ left (1-e ^ {- \ lambda / \ theta} \ right) \ left (e ^ {- \ lambda / \ theta } \ dreapta) ^ {n}.}

Distribuția Poisson ${\mathcal {P}}(\lambda )$ ${\ displaystyle {\ mathcal {P}} (\ lambda)}$ ${\ mathcal {P}} (\ lambda)$ descrie numărul de evenimente succesive care au avut loc într-un interval de timp, în care timpul de așteptare între două evenimente ulterioare este independent și este reglementat de distribuția exponențială a aceluiași parametru $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ .

Distribuția exponențială ${\mathcal {E}}\left({\tfrac {1}{2}}\right)$ ${\ displaystyle {\ mathcal {E}} \ left ({\ tfrac {1} {2}} \ right)}$ ${\ displaystyle {\ mathcal {E}} \ left ({\ tfrac {1} {2}} \ right)}$ corespunde distribuției chi-pătrat cu două grade de libertate, $\chi ^{2}(2)$ ${\ displaystyle \ chi ^ {2} (2)}$ $\ chi ^ {2} (2)$ .

Distribuția Laplace a parametrilor $(\mu ,b)$ ${\ displaystyle (\ mu, b)}$ $(\ mu, b)$ guvernează variabila aleatorie $Y=\mu +X_{1}-X_{2}$ ${\ displaystyle Y = \ mu + X_ {1} -X_ {2}}$ $Y = \ mu + X_ {1} -X_ {2}$ , unde este $X_{1},X_{2}$ ${\ displaystyle X_ {1}, X_ {2}}$ $X_ {1}, X_ {2}$ sunt două variabile aleatoare independente cu aceeași distribuție exponențială ${\mathcal {E}}(1/b)$ ${\ displaystyle {\ mathcal {E}} (1 / b)}$ ${\ mathcal {E}} (1 / b)$ .

Distribuția Gamma generalizează distribuția exponențială: $\Gamma (1,\lambda )$ ${\ displaystyle \ Gamma (1, \ lambda)}$ $\ Gamma (1, \ lambda)$ coincide cu ${\mathcal {E}}(\lambda )$ ${\ displaystyle {\ mathcal {E}} (\ lambda)}$ ${\ mathcal {E}} (\ lambda)$ . În special, suma $Y=X_{1}+\dots +X_{n}$ ${\ displaystyle Y = X_ {1} + \ dots + X_ {n}}$ $Y = X_ {1} + \ dots + X_ {n}$ din $n$ ${\ displaystyle n}$ $n$ variabile aleatorii independente ale aceleiași legi exponențiale cu parametrul $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ urmează distribuția Gamma $\Gamma (n,\lambda )$ ${\ displaystyle \ Gamma (n, \ lambda)}$ $\ Gamma (n, \ lambda)$ . De asemenea, în inferența bayesiană dacă parametrul $\lambda$ ${\ displaystyle \ lambda}$ $\ lambda$ urmează o distribuție exponențială, a priori a unei observații, o distribuție Gamma, apoi o distribuție Gamma urmează și a posteriori .

Aplicații

Radioactivitate

Timpul de descompunere al unui izotop radioactiv este de obicei modelat ca o funcție a vieții sale medii prin distribuția exponențială ${\mathcal {E}}(1/\tau )$ ${\ displaystyle {\ mathcal {E}} (1 / \ tau)}$ ${\ mathcal {E}} (1 / \ tau)$ .

În acest cadru, parametrul $\lambda =1/\tau$ ${\ displaystyle \ lambda = 1 / \ tau}$ $\ lambda = 1 / \ tau$ se numește constanta de descompunere ; speranța de viață este corectă $E[X]=1/\lambda =\tau$ ${\ displaystyle E [X] = 1 / \ lambda = \ tau}$ $E [X] = 1 / \ lambda = \ tau$ .

Cu acest model, de exemplu, este posibil să se calculeze probabilitățile ca izotopul să se descompună în mai puțin de jumătate din timpul mediu,

P(T<{\tfrac {1}{2}}\tau )=F({\tfrac {1}{2}}\tau )=1-e^{-\lambda {\frac {1}{2}}\tau }=1-e^{-{\frac {1}{2}}}\approx 0,393

{\ displaystyle P (T <{\ tfrac {1} {2}} \ tau) = F ({\ tfrac {1} {2}} \ tau) = 1-e ^ {- \ lambda {\ frac {1 } {2}} \ tau} = 1-e ^ {- {\ frac {1} {2}}} \ aproximativ 0,393}

P (T <{\ tfrac {1} {2}} \ tau) = F ({\ tfrac {1} {2}} \ tau) = 1-e ^ {{- \ lambda {\ frac {1} { 2}} \ tau}} = 1-e ^ {{- {\ frac {1} {2}}}} \ aproximativ 0,393

,

sau mai mult decât dublu de data aceasta

P(T>2\tau )=1-F(2\tau )=e^{-\lambda \tau }=e^{-2}\approx 0,135

{\ displaystyle P (T> 2 \ tau) = 1-F (2 \ tau) = e ^ {- \ lambda \ tau} = e ^ {- 2} \ approx 0.135}

P (T> 2 \ tau) = 1-F (2 \ tau) = e ^ {{- \ lambda \ tau}} = e ^ {{- 2}} \ aprox 0.135

.

De exemplu, prin formula cuantilă se constată că numai cu o probabilitate de douăzeci, izotopul se va descompune în mai mult de

q_{1-1/20}={\tfrac {1}{\lambda }}\log 20\approx 3\tau

{\ displaystyle q_ {1-1 / 20} = {\ tfrac {1} {\ lambda}} \ log 20 \ approx 3 \ tau}

q _ {{1-1 / 20}} = {\ tfrac {1} {\ lambda}} \ log 20 \ approx 3 \ tau

.

Cu toate acestea, un observator care nu a văzut încă izotopul se descompune după o perioadă de $3\tau$ ${\ displaystyle 3 \ tau}$ $3 \ tau$ se regăsește din nou în condițiile inițiale, din cauza absenței memoriei; va trebui, așadar, să aștepte un timp mediu $\tau$ ${\ displaystyle \ tau}$ $\ tau$ înainte de decădere.

Într-un eșantion cu un număr foarte mare de izotopi (așa cum se întâmplă de obicei), probabilitățile fiecărui izotop individual (independent de celelalte) pot fi traduse în procente din eșantion. De exemplu, timpul mediu după care jumătate din probe se descompun ( timpul de înjumătățire sau timpul de înjumătățire ) este dat de mediana $q_{1/2}=(\log 2)/\lambda$ ${\ displaystyle q_ {1/2} = (\ log 2) / \ lambda}$ $q _ {{1/2}} = (\ log 2) / \ lambda$ .

Elemente conexe

Alte proiecte

Wikimedia Commons conține imagini sau alte fișiere despre distribuția exponențială

linkuri externe

(EN) Eric W. Weisstein, distribuție exponențială , în MathWorld Wolfram Research.

Controlul autorității	GND ( DE ) 4016019-1

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică