Relația de comandă

În matematică , mai exact în teoria ordinii, o relație de ordine a unei mulțimi este o relație binară între elementele aparținând mulțimii care are următoarele proprietăți:

Un set parțial ordonat (sau ordine ) este definit ca perechea constând dintr-un set și o relație de ordine pe acesta. Relațiile de ordine sunt adesea indicate cu simboluri $\leq$ ${\ displaystyle \ leq}$ $\ leq$ , $\subseteq$ ${\ displaystyle \ subseteq}$ $\ subseteq$ , $\sqsubseteq$ ${\ displaystyle \ sqsubseteq}$ $\ sqsubseteq$ Și $\preccurlyeq$ ${\ displaystyle \ preccurlyeq}$ $\ preccurlyeq$ .

În limba engleză, un set parțial ordonat este, de asemenea, numit concis poset ( Set Parțial ordonat ), iar acest termen este folosit și jargon în limba italiană.

Definiție

Având două seturi $LA$ ${\ displaystyle A}$ $LA$ Și $B.$ ${\ displaystyle B}$ $B.$ , produsul lor cartezian este setul de perechi ordonate definit astfel: ^[1]

A\times B:=\{(a,b):a\in A\;\mathrm {e} \;b\in B\}\

{\ displaystyle A \ times B: = \ {(a, b): a \ in A \; \ mathrm {e} \; b \ in B \} \}

A \ times B: = \ {(a, b): a \ in A \; {\ mathrm {e}} \; b \ in B \} \

Se numește relație binară pe un set $LA$ ${\ displaystyle A}$ $LA$ un subset $R.$ ${\ displaystyle R}$ $R.$ a produsului cartezian $A\times A$ ${\ displaystyle A \ times A}$ $A \ ori A$ . ^[2] Două elemente $X$ ${\ displaystyle x}$ $X$ Și $y$ ${\ displaystyle y}$ $y$ sunt legate de $R.$ ${\ displaystyle R}$ $R.$ de sine:

(x,y)\in R\

{\ displaystyle (x, y) \ în R \}

(x, y) \ în R \

iar în acest caz este scris $X R. y$ ${\ displaystyle xRy}$ ${\ displaystyle xRy}$ .

O relație de ordine $\leq$ ${\ displaystyle \ leq}$ $\ leq$ este o relație binară între elementele unui set $LA$ ${\ displaystyle A}$ $LA$ reflexiv , antisimetric și tranzitiv . ^[3]

În mod explicit, această relație îndeplinește următoarele proprietăți:

x\leq x\quad \forall x\in A

{\ displaystyle x \ leq x \ quad \ forall x \ în A}

x \ leq x \ quad \ forall x \ în A

[x\leq y\land y\leq x]\implies x=y\quad \forall x,y\in A

{\ displaystyle [x \ leq y \ land y \ leq x] \ implică x = y \ quad \ forall x, y \ în A}

{\ displaystyle [x \ leq y \ land y \ leq x] \ implică x = y \ quad \ forall x, y \ in A}

{\textstyle [x\leq y\land y\leq z]\implies x\leq z\quad \forall x,y,z\in A}

{\ textstyle [x \ leq y \ land y \ leq z] \ implică x \ leq z \ quad \ forall x, y, z \ in A}

{\ textstyle [x \ leq y \ land y \ leq z] \ implică x \ leq z \ quad \ forall x, y, z \ in A}

Relațiile de ordine sunt adesea indicate cu simboluri $\leq$ ${\ displaystyle \ leq}$ $\ leq$ , $\subseteq$ ${\ displaystyle \ subseteq}$ $\ subseteq$ , $\sqsubseteq$ ${\ displaystyle \ sqsubseteq}$ $\ sqsubseteq$ Și $\preccurlyeq$ ${\ displaystyle \ preccurlyeq}$ $\ preccurlyeq$ .

Cuplul $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ constituit dintr-un set și o relație de ordine pe acesta se numește set parțial ordonat sau pur și simplu ordine , care nu trebuie confundat cu termenul mai specific mulțime total ordonată .

Primele exemple

Exemple bine cunoscute de seturi parțial ordonate sunt:

seturi numerice $\mathbb {N}$ ${\ displaystyle \ mathbb {N}}$ $\ mathbb N$ , $\mathbb {Z}$ ${\ displaystyle \ mathbb {Z}}$ $\ mathbb {Z}$ , $\mathbb {Q}$ ${\ displaystyle \ mathbb {Q}}$ ${\ mathbb Q}$ , $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb R$ cu raportul standard total al comenzii $aRb\Leftrightarrow a\leq b$ ${\ displaystyle aRb \ Leftrightarrow a \ leq b}$ $aRb \ Leftrightarrow a \ leq b$ ,
întregul $\mathbb {N} \backslash \{0\}$ ${\ displaystyle \ mathbb {N} \ backslash \ {0 \}}$ ${\ mathbb N} \ backslash \ {0 \}$ a furnizat raportul de divizibilitate $aRb\Leftrightarrow a|b$ ${\ displaystyle aRb \ Leftrightarrow a | b}$ $aRb \ Leftrightarrow a | b$ (acesta este $la$ ${\ displaystyle a}$ $la$ este divizorul lui $b$ ${\ displaystyle b}$ $b$ )

Orice familie de seturi cu relația de incluziune $aRb\Leftrightarrow a\subseteq b$ ${\ displaystyle aRb \ Leftrightarrow a \ subseteq b}$ $aRb \ Leftrightarrow a \ subseteq b$ (acesta este $la$ ${\ displaystyle a}$ $la$ este un subset de $b$ ${\ displaystyle b}$ $b$ )

Ordinea largă și ordinea îngustă

Unii autori ^[4] definesc o relație de ordine „strânsă” ca o relație $(A,<)$ ${\ displaystyle (A, <)}$ ${\ displaystyle (A, <)}$ care satisface proprietățile antiflexive , antisimetrice și tranzitive (sau, echivalent și mai concis, proprietățile asimetrice și tranzitive ) și, prin urmare, numesc relația de ordine „largă” $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ ${\ displaystyle (A, \ leq)}$ . Ordinea strictă își propune să se concentreze pe asimetria relației, fără a lua în considerare reflexivitatea.

Deși cele două definiții sunt distincte, studiul lor nu prezintă diferențe majore, deoarece există o corespondență foarte simplă unu la unu între cele două clase de relații.

Este $LA$ ${\ displaystyle A}$ $LA$ un set și denotați cu $\,\Delta (A)$ ${\ displaystyle \, \ Delta (A)}$ ${\ displaystyle \, \ Delta (A)}$ diagonala de $\,A\times A$ ${\ displaystyle \, A \ times A}$ ${\ displaystyle \, A \ times A}$ , acesta este $\ \Delta (A):=\{(x,x):x\in A\}$ ${\ displaystyle \ \ Delta (A): = \ {(x, x): x \ în A \}}$ ${\ displaystyle \ \ Delta (A): = \ {(x, x): x \ în A \}}$ , apoi la fiecare relație de ordine largă $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ ${\ displaystyle (A, \ leq)}$ relația de ordine strânsă este asociată $(A,\leq )\setminus \Delta (A)$ ${\ displaystyle (A, \ leq) \ setminus \ Delta (A)}$ ${\ displaystyle (A, \ leq) \ setminus \ Delta (A)}$ ; invers la orice relație de ordin strict $(A,<)$ ${\ displaystyle (A, <)}$ ${\ displaystyle (A, <)}$ relația de ordine mare este asociată $(A,<)\cup \Delta (A)$ ${\ displaystyle (A, <) \ cup \ Delta (A)}$ ${\ displaystyle (A, <) \ cup \ Delta (A)}$ .

Digraful unui ordin

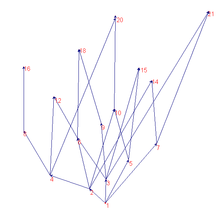
Graficul relației de divizibilitate

Dacă întregul $LA$ ${\ displaystyle A}$ $LA$ este finit sau numărabil , relația de ordine poate fi reprezentată vizual prin intermediul unui digraf (respectiv finit sau numărabil) ale cărui noduri sunt elementele $LA$ ${\ displaystyle A}$ $LA$ și astfel încât două noduri $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ sunt conectate printr-un arc dacă și numai dacă $a\leq b$ ${\ displaystyle a \ leq b}$ $a \ leq b$ și nu există elemente intermediare între ele (adică nu există $c\neq a,b$ ${\ displaystyle c \ neq a, b}$ $c \ neq a, b$ astfel încât $a\leq c$ ${\ displaystyle a \ leq c}$ $a \ leq c$ Și $c\leq b$ ${\ displaystyle c \ leq b}$ $c \ leq b$ ). Graficul unei relații de ordine nu poate avea cicluri , în timp ce poate avea mai multe componente conectate și orice număr de margini poate intra și ieși din fiecare dintre nodurile sale. Dacă graficul poate fi numărat, arcul infinit poate intra sau ieși dintr-un nod (acesta este cazul relației de divizibilitate).

Comenzi simple, liniare și totale

Două elemente $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ a unui set parțial ordonat $\,(A,\leq )\,$ ${\ displaystyle \, (A, \ leq) \,}$ ${\ displaystyle \, (A, \ leq) \,}$ se spune că sunt comparabile dacă se întâmplă acest lucru $a\leq b$ ${\ displaystyle a \ leq b}$ $a \ leq b$ sau asta $b\leq a$ ${\ displaystyle b \ leq a}$ $b \ leq a$ .

În general, două elemente ale unei relații de ordine parțială pot să nu fie comparabile, adică nu sunt neapărat legate între ele. De exemplu în $\mathbb {N} \backslash \{0\}$ ${\ displaystyle \ mathbb {N} \ backslash \ {0 \}}$ ${\ mathbb N} \ backslash \ {0 \}$ prevăzut cu relația de divizibilitate, elementele 2 și 3 nu sunt legate, deoarece niciunul dintre ele nu este divizor al celuilalt.

Un set se numește o ordine simplă sau liniară sau o ordine totală pentru fiecare $a,b\in A$ ${\ displaystyle a, b \ în A}$ $a, b \ în A$ , $la$ ${\ displaystyle a}$ $la$ Și ${\textstyle b}$ ${\ textstyle b}$ ${\ textstyle b}$ sunt comparabile (adică merită $a\leq b$ ${\ displaystyle a \ leq b}$ $a \ leq b$ sau $b\leq a$ ${\ displaystyle b \ leq a}$ $b \ leq a$ ).

Digraful unui set total ordonat poate fi reprezentat ca un segment sau o linie sau o rază pe care se află toate nodurile (corespunzătoare tuturor elementelor setului).

Lanțuri și anticatenuri

Fii o comandă $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ , fiecare subset se numește lanț $Y\subseteq A$ ${\ displaystyle Y \ subseteq A}$ ${\ displaystyle Y \ subseteq A}$ astfel încât relația de ordine s-a redus la $Da$ ${\ displaystyle Y}$ $Da$ constituie o simplă ordine .

În schimb, se numește anticaten al întregului parțial ordonat $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ un subset $Y\subseteq A$ ${\ displaystyle Y \ subseteq A}$ ${\ displaystyle Y \ subseteq A}$ ale căror elemente sunt incompatibile reciproc. Un anticaten al setului parțial ordonat de divizibilități este furnizat de setul de numere prime.

Exemplu

Pentru setul de divizibilitate parțial ordonat, lanțurile sunt mulțimile puterilor pozitive ale unui număr prim și mai general subseturile obținute cu un proces care începe prin a considera un număr întreg pozitiv și continuă prin adăugarea la fiecare pas a unui multiplu al numărului întreg adăugat anterior. Ele pot fi considerate lanțuri finite sau infinite; procesul anterior poate fi finit sau nelimitat.

Majoritate și minoritate

Este $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ a order (poset) e $\emptyset \neq S\subseteq A$ ${\ displaystyle \ emptyset \ neq S \ subseteq A}$ ${\ displaystyle \ emptyset \ neq S \ subseteq A}$ . Apoi se spune că un element $y\in A$ ${\ displaystyle y \ în A}$ ${\ displaystyle y \ în A}$ este o majoritate a $S.$ ${\ displaystyle S}$ $S.$ de sine $\forall x\in S,\ x\leq y$ ${\ displaystyle \ forall x \ în S, \ x \ leq y}$ $\ forall x \ în S, \ x \ leq y$ .

În mod similar, într-un mod dual, un element $y\in A$ ${\ displaystyle y \ în A}$ ${\ displaystyle y \ în A}$ este definit ca o minoritate a unui set $S.$ ${\ displaystyle S}$ $S.$ de sine $\forall x\in S,\ y\leq x$ ${\ displaystyle \ forall x \ în S, \ y \ leq x}$ $\ forall x \ in S, \ y \ leq x$ .

De sine $S.$ ${\ displaystyle S}$ $S.$ admite cel puțin un majorant (minoritate) atunci se spune că $S.$ ${\ displaystyle S}$ $S.$ este un subset delimitat deasupra (dedesubt).

Se spune că un subset care are atât majore cât și minore este limitat în ordine .

Dacă întregul $S.$ ${\ displaystyle S}$ $S.$ este un set numeric cu cardinalitate mai mare decât unul ( $|S|>1$ ${\ displaystyle | S |> 1}$ $| S |> 1$ ) alegând apoi un subset al acestuia $S_{2}\subseteq S$ ${\ displaystyle S_ {2} \ subseteq S}$ $S_ {2} \ subseteq S$ cu cardinalitate de 2 ( $|S_{2}|=2$ ${\ displaystyle | S_ {2} | = 2}$ $| S_ {2} | = 2$ ), putem defini minimul între cele două elemente, $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ cu următoarea relație:

\min\{a,b\}=\mathbf {1} _{\mathbb {R} ^{-}}(a-b)\cdot (a-b)+b

{\ displaystyle \ min \ {a, b \} = \ mathbf {1} _ {\ mathbb {R} ^ {-}} (ab) \ cdot (ab) + b}

\ min \ {a, b \} = {\ mathbf {1}} _ {{{\ mathbb {R}} ^ {-}}} (a-b) \ cdot (a-b) + b

Maximul dintre cele două elemente se găsește în schimb cu următoarea expresie

\max\{a,b\}=\mathbf {1} _{\mathbb {R} ^{+}}(a-b)\cdot (a-b)+b

{\ displaystyle \ max \ {a, b \} = \ mathbf {1} _ {\ mathbb {R} ^ {+}} (ab) \ cdot (ab) + b}

\ max \ {a, b \} = {\ mathbf {1}} _ {{{\ mathbb {R}} ^ {+}}} (a-b) \ cdot (a-b) + b

Unde cu $\mathbf {1}$ ${\ displaystyle \ mathbf {1}}$ ${\ displaystyle \ mathbf {1}}$ funcția indicator a fost indicată.

Elemente maxime și minime

Este $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ un ordin. Se spune că $m$ ${\ displaystyle m}$ $m$ este elementul minim al $LA$ ${\ displaystyle A}$ $LA$ de sine $\forall a\in A,\ m\leq a$ ${\ displaystyle \ forall a \ în A, \ m \ leq a}$ ${\ displaystyle \ forall a \ în A, \ m \ leq a}$ .

Element maxim de $LA$ ${\ displaystyle A}$ $LA$ A $y\in A$ ${\ displaystyle y \ în A}$ $y \ în A$ astfel încât $\forall a\in A,\ a\leq y$ ${\ displaystyle \ forall a \ în A, \ a \ leq y}$ ${\ displaystyle \ forall a \ în A, \ a \ leq y}$ .

Există tipuri pentru care nu există un element minim (respectiv maxim); se arată cu ușurință că, dacă există un element minim (respectiv maxim), acesta este unic. Când există, elementul maxim și elementul minim al $LA$ ${\ displaystyle A}$ $LA$ sunt indicate respectiv ca max $LA$ ${\ displaystyle A}$ $LA$ și min $LA$ ${\ displaystyle A}$ $LA$ .

La comenzi non-simple este util să se definească alte două concepte: cel de element minim și maxim.

$m$ ${\ displaystyle m}$ $m$ se spune că este un element minim al $LA$ ${\ displaystyle A}$ $LA$ de sine $a\in A,\ a\leq m\;\Rightarrow \;a=m$ ${\ displaystyle a \ în A, \ a \ leq m \; \ Rightarrow \; a = m}$ ${\ displaystyle a \ în A, \ a \ leq m \; \ Rightarrow \; a = m}$ ;

$M.$ ${\ displaystyle M}$ $M.$ în schimb va fi un element de tavan dacă $a\in A,\ M\leq a\;\Rightarrow \;a=M$ ${\ displaystyle a \ în A, \ M \ leq a \; \ Rightarrow \; a = M}$ ${\ displaystyle a \ în A, \ M \ leq a \; \ Rightarrow \; a = M}$ .

În general, elementul maxim și maxim nu corespund aceluiași element. Luați în considerare întregul ca exemplu $\{2,3,4,5,6\}$ ${\ displaystyle \ {2,3,4,5,6 \}}$ $\ {2,3,4,5,6 \}$ prevăzut cu relația de divizibilitate: nu admite nici maxim, nici minim, dar de exemplu 3 este un element minim, deoarece $x|3$ ${\ displaystyle x | 3}$ $x | 3$ este mulțumit doar pentru $x=3$ ${\ displaystyle x = 3}$ $x = 3$ . De asemenea, rețineți că elementul 3 nu poate fi maxim. Dacă da, atunci 3 nu ar împărți niciun alt element al setului, ci $3|6$ ${\ displaystyle 3 | 6}$ $3 | 6$ ceea ce dovedește absurdul afirmației având în vedere că $3\neq 6$ ${\ displaystyle 3 \ neq 6}$ $3 \ neq 6$ . Chiar și 5 este atât un element maxim, cât și un element minim, deoarece nu este legat de niciun alt element al întregului decât el însuși. Din exemplu, este ușor de înțeles că cele două definiții (element maxim și maxim; element minim și minim) coincid în prezența unei ordini simple.

Extremele superioare și inferioare

Este $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ o comandă și fie ea $\emptyset \neq S\subseteq A$ ${\ displaystyle \ emptyset \ neq S \ subseteq A}$ ${\ displaystyle \ emptyset \ neq S \ subseteq A}$ . Definim:

$M_{S}=\{x\in A\,|\,{x}\;{e'}\;{maggiorante}\;{di}\;S\}$ ${\ displaystyle M_ {S} = \ {x \ în A \, | \, {x} \; {e '} \; {majorant} \; {di} \; S \}}$ ${\ displaystyle M_ {S} = \ {x \ în A \, | \, {x} \; {e '} \; {majorant} \; {di} \; S \}}$ ;

$m_{s}=\{x\in A\,|\,{x}\;{e'}\;{minorante}\;{di}\;S\}$ ${\ displaystyle m_ {s} = \ {x \ în A \, | \, {x} \; {e '} \; {minoritate} \; {di} \; S \}}$ ${\ displaystyle m_ {s} = \ {x \ în A \, | \, {x} \; {e '} \; {minoritate} \; {di} \; S \}}$ .

Apoi se definesc:

vârf extrem de $S.$ ${\ displaystyle S}$ $S.$ the $\min M_{S}$ ${\ displaystyle \ min M_ {S}}$ $\ min M_ {S}$ ; când există este indicat cu ${sup}\;S$ ${\ displaystyle {sup} \; S}$ ${sup} \; S$ ;

limita inferioară a $S.$ ${\ displaystyle S}$ $S.$ the $\max m_{S}$ ${\ displaystyle \ max m_ {S}}$ $\ max m_ {S}$ ; când există este indicat cu ${inf}\;S$ ${\ displaystyle {inf} \; S}$ ${inf} \; S$ .

Observăm că, având în vedere un subset, nu se spune că admite un minim sau un maxim și, prin urmare, nu se spune că există extreme superioare și inferioare.

Segmente inițiale și finale

Este $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ $(A, \ leq)$ un set ordonat și un subset $S\subseteq A$ ${\ displaystyle S \ subseteq A}$ ${\ displaystyle S \ subseteq A}$ , asa de $S.$ ${\ displaystyle S}$ $S.$ si a zis:

segmentul inițial al $LA$ ${\ displaystyle A}$ $LA$ , dacă sunt date două elemente $x\in S$ ${\ displaystyle x \ în S}$ $x \ în S$ Și $y\in A$ ${\ displaystyle y \ în A}$ $y \ în A$ , avem asta $y\leq x\Rightarrow y\in S$ ${\ displaystyle y \ leq x \ Rightarrow y \ in S}$ ${\ displaystyle y \ leq x \ Rightarrow y \ in S}$ ;
segmentul final al $LA$ ${\ displaystyle A}$ $LA$ , dacă este similar $x\leq y\Rightarrow y\in S$ ${\ displaystyle x \ leq y \ Rightarrow y \ în S}$ ${\ displaystyle x \ leq y \ Rightarrow y \ în S}$ .

Cu alte cuvinte, elementele da $S.$ ${\ displaystyle S}$ $S.$ nu permite (respectiv) minim sau maxim în afara $S.$ ${\ displaystyle S}$ $S.$ .

Sisteme juridice bine întemeiate

O relație de ordine pe un set $LA$ ${\ displaystyle A}$ $LA$ spunem „bine întemeiat” sau bună ordine dacă fiecare subset $Da$ ${\ displaystyle Y}$ $Da$ $\subseteq$ ${\ displaystyle \ subseteq}$ $\ subseteq$ $LA$ ${\ displaystyle A}$ $LA$ nu gol este echipat cu un minim.

Un exemplu tipic de bună ordonare este cel care stabilește relația de ordine standard pe ansamblu $\mathbb {N}$ ${\ displaystyle \ mathbb {N}}$ $\ mathbb N$ a numerelor naturale. Afirmația că naturile sunt un set bine ordonat, adică fiecare subset $X$ ${\ displaystyle X}$ $X$ din $\mathbb {N}$ ${\ displaystyle \ mathbb {N}}$ $\ mathbb N$ are un minimum este uneori numit principiul bunei ordine și se poate dovedi a fi echivalent cu principiul inducției .

Teorema bunei ordonări

Teorema bunei ordonări (nu trebuie confundată cu principiul bunei ordonări ) afirmă că o relație de ordine bine întemeiată (sau o bună ordonare) poate fi definită pe orice set ne-gol. Această afirmație este echivalentă cu axioma alegerii (adică presupunând că este adevărată putem demonstra axioma alegerii și invers).

Produs cartezian al comenzilor

Produsul cartezian din două seturi parțial comandate poate fi, de asemenea, furnizat cu o comandă în mai multe moduri:

conform criteriului ordinii lexicografice

conform comparației „termen la termen” $(a_{1},b_{1})\leq (a_{2},b_{2})$ ${\ displaystyle (a_ {1}, b_ {1}) \ leq (a_ {2}, b_ {2})}$ $(a_ {1}, b_ {1}) \ leq (a_ {2}, b_ {2})$ de sine $a_{1}\leq a_{2}$ ${\ displaystyle a_ {1} \ leq a_ {2}}$ $a_ {1} \ leq a_ {2}$ Și $b_{1}\leq b_{2}$ ${\ displaystyle b_ {1} \ leq b_ {2}}$ $b_ {1} \ leq b_ {2}$ (ordinea astfel formată se numește produsul direct al celor două ordine)

conform raportului $(a_{1},b_{1})\leq (a_{2},b_{2})$ ${\ displaystyle (a_ {1}, b_ {1}) \ leq (a_ {2}, b_ {2})}$ $(a_ {1}, b_ {1}) \ leq (a_ {2}, b_ {2})$ de sine $a_{1}<a_{2}\wedge b_{1}<b_{2}$ ${\ displaystyle a_ {1} <a_ {2} \ wedge b_ {1} <b_ {2}}$ $a_ {1} <a_ {2} \ wedge b_ {1} <b_ {2}$ sau $a_{1}=a_{2}\wedge b_{1}=b_{2}$ ${\ displaystyle a_ {1} = a_ {2} \ wedge b_ {1} = b_ {2}}$ $a_ {1} = a_ {2} \ wedge b_ {1} = b_ {2}$

Dacă cele două ordine sunt simple, la fel este și ordinea lexicografică, dar nu neapărat celelalte două.

Funcții și relații de ordine

Lasa-i sa fie $(A,\leq )$ ${\ displaystyle (A, \ leq)}$ ${\ displaystyle (A, \ leq)}$ Și $(P,\preccurlyeq )$ ${\ displaystyle (P, \ preccurlyeq)}$ $(P, \ preccurlyeq)$ două ordine și ambele $f\colon A\to P$ ${\ displaystyle f \ colon A \ to P}$ ${\ displaystyle f \ colon A \ to P}$ .

$f$ ${\ displaystyle f}$ $f$ se spune monoton dacă $x\leq y\Rightarrow f(x)\preccurlyeq f(y)$ ${\ displaystyle x \ leq y \ Rightarrow f (x) \ preccurlyeq f (y)}$ $x \ leq y \ Rightarrow f (x) \ preccurlyeq f (y)$ pentru fiecare x, y în $P.$ ${\ displaystyle P}$ $P.$ .

$f$ ${\ displaystyle f}$ $f$ se spune antiton dacă $x\leq y\Rightarrow f(x)\succcurlyeq f(y)$ ${\ displaystyle x \ leq y \ Rightarrow f (x) \ succcurlyeq f (y)}$ $x \ le y \ Rightarrow f (x) \ succcurlyeq f (y)$ pentru fiecare x, y în $P.$ ${\ displaystyle P}$ $P.$ .

Notă

^ Reed, Simon , Pagina 1 .
^ Reed, Simon , Pagina 2 .
^ Reed, Simon , Pagina 3 .
^ Vincenzo Aversa, Metode cantitative de decizii. Algebra și analiza elementară într-o selecție de probleme de alegere , în manuale pentru universitate , Liguori Editore, 2000, pp. 12-15, ISBN 9788820731649 .

Bibliografie

Michael Reed, Barry Simon, Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis , ed. A II-a, San Diego, California, Academic press inc., 1980, ISBN 0-12-585050-6 .

Elemente conexe

Total ordonate împreună
Relația rețelei și a rețelei de rețea (matematică)
Ordine densă
Arborescență sau copac înrădăcinat
Teoria graficelor
Relația de echivalență
Pre-comanda
Extrema superioară
Starea lanțului ascendent
Grup ordonat , câmp ordonat, spațiu vector ordonat

Controlul autorității	GND ( DE ) 4172733-2

Portalul de matematică : accesați intrările Wikipedia care se ocupă de matematică

[1] Reed, Simon , Pagina 1 .

[2] Reed, Simon , Pagina 2 .

[3] Reed, Simon , Pagina 3 .

[:0-4] Vincenzo Aversa, Metode cantitative de decizii. Algebra și analiza elementară într-o selecție de probleme de alegere , în manuale pentru universitate , Liguori Editore, 2000, pp. 12-15, ISBN 9788820731649 .

[1]

[2]

[3]

[4]