Funcție continuă

Funcția în roșu este continuă, cea în albastru nu

În matematică , o funcție continuă este o funcție care, intuitiv, se potrivește în mod arbitrar cu elemente apropiate ale intervalului cu elemente suficient de apropiate ale domeniului.

Există definiții diferite ale continuității, corespunzătoare contextelor matematice în care sunt utilizate: continuitatea unei funcții este unul dintre conceptele de bază ale topologiei și analizei matematice . Continuitatea unei funcții poate fi definită și local: în acest caz vorbim de continuitate într-un punct al domeniului. O funcție continuă este, prin definiție, continuă în fiecare punct al domeniului său. O funcție care nu este continuă se numește discontinuă , iar punctele din domeniul în care nu este continuă se numesc puncte de discontinuitate .

De exemplu, funcția $h(t)$ ${\ displaystyle h (t)}$ $h (t)$ descrierea înălțimii unui bărbat față de vârsta sa poate fi văzută ca o funcție continuă: în perioade scurte omul crește puțin. Dimpotrivă, funcția $g(t)$ ${\ displaystyle g (t)}$ $g (t)$ reprezentarea sumei de bani într-un cont curent de-a lungul timpului este o funcție discontinuă, deoarece retragerile și depunerile îi determină să sară de la o valoare la alta.

Definiții

Continuitatea unei funcții este un concept topologic și, prin urmare, definiția generală a unei funcții continue se dezvoltă cu funcții între spații topologice. Cu toate acestea, același concept este utilizat în zone mai puțin generale, în special în ceea ce privește utilizarea sa în analiza matematică : definiția continuității este adesea prezentată numai pentru funcții între spații metrice sau, din nou, numai pentru funcții ale unei variabile reale.

Funcții reale

Graficul funcției are un salt în x ₀ : funcția nu este continuă

În cazul funcțiilor unei variabile reale, continuitatea este adesea prezentată ca o proprietate a graficului: funcția este continuă dacă graficul său este format dintr-o singură curbă care nu face niciodată salturi. Deși această noțiune poate fi utilizată în cazuri mai simple pentru a distinge funcțiile continue de funcțiile discontinue, nu este formal corectă și poate duce la ambiguitate sau erori.

Definiție în termeni de limită a unei funcții

O functie $f$ ${\ displaystyle f}$ $f$ este definit ca continuu la punct $p$ ${\ displaystyle p}$ $p$ a domeniului său dacă limita sa pentru $X$ ${\ displaystyle x}$ $X$ tinde să $p$ ${\ displaystyle p}$ $p$ coincide cu evaluarea funcției în $p$ ${\ displaystyle p}$ $p$ , asta este cu $f(p)$ ${\ displaystyle f (p)}$ $f (p)$ . În simboluri: ^[1]

\lim _{x\to p}f(x)=f(p)

{\ displaystyle \ lim _ {x \ to p} f (x) = f (p)}

\ lim_ {x \ to p} f (x) = f (p)

Această definiție este folosită mai ales pentru funcții definite pe un interval al liniei reale: de fapt, are sens doar dacă $p$ ${\ displaystyle p}$ $p$ este un punct de acumulare pentru domeniul $f$ ${\ displaystyle f}$ $f$ . Cu toate acestea, poate fi extins și în cazul domeniilor mai complicate, care includ puncte izolate: în ele, $f$ ${\ displaystyle f}$ $f$ rezultă continuu pentru un „adevăr gol” (din engleza vacuous adevăr ).

Se spune că funcția este continuă dacă este continuă în orice punct $p$ ${\ displaystyle p}$ $p$ a domeniului.

Definiția epsilon-delta

Studiind funcția din punct

p=2

{\ displaystyle p = 2}

p = 2

, și alegerea

\varepsilon =0.5

{\ displaystyle \ varepsilon = 0,5}

\ varepsilon = 0,5

, doar alege

\delta =0.5

{\ displaystyle \ delta = 0,5}

\ delta = 0,5

pentru a face toate imaginile punctelor din

(2-\delta ,2+\delta )

{\ displaystyle (2- \ delta, 2 + \ delta)}

(2- \ delta, 2 + \ delta)

distins pentru mai puțin de

\epsilon

{\ displaystyle \ epsilon}

\ epsilon

din

f(2)=3.5

{\ displaystyle f (2) = 3.5}

f (2) = 3,5

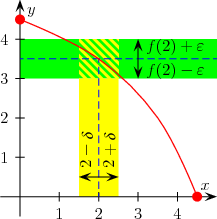
O functie $f\colon A\rightarrow \mathbb {R}$ ${\ displaystyle f \ colon A \ rightarrow \ mathbb {R}}$ $f \ colon A \ rightarrow \ mathbb {R}$ definit pe un subset $LA$ ${\ displaystyle A}$ $LA$ se spune că numerele reale cu valori reale sunt continue la un moment dat $p\in A$ ${\ displaystyle p \ în A}$ $p \ în A$ dacă pentru orice număr $\varepsilon >0$ ${\ displaystyle \ varepsilon> 0}$ $\ varepsilon> 0$ , în mod arbitrar mic, există un al doilea număr $\delta >0$ ${\ displaystyle \ delta> 0}$ $\ delta> 0$ astfel încât, $\forall x\in A\cap (p-\delta ,p+\delta )$ ${\ displaystyle \ forall x \ in A \ cap (p- \ delta, p + \ delta)}$ $\ forall x \ in A \ cap (p- \ delta, p + \ delta)$ , functia $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este departe de $f(p)$ ${\ displaystyle f (p)}$ $f (p)$ pentru mai puțin de $\varepsilon$ ${\ displaystyle \ varepsilon}$ $\ varepsilon$ , adică: ^[1]

|f(x)-f(p)|<\varepsilon

{\ displaystyle | f (x) -f (p) | <\ varepsilon}

| f (x) - f (p) | <\ varepsilon

În limbajul simbolic, o funcție este continuă la un moment dat $p$ ${\ displaystyle p}$ $p$ de sine:

\forall \varepsilon >0\ \exists \delta >0:|x-p|<\delta \Rightarrow |f(x)-f(p)|<\varepsilon

{\ displaystyle \ forall \ varepsilon> 0 \ \ există \ delta> 0: | xp | <\ delta \ Rightarrow | f (x) -f (p) | <\ varepsilon}

\ forall \ varepsilon> 0 \ \ exist \ delta> 0: | x-p | <\ delta \ Rightarrow | f (x) -f (p) | <\ varepsilon

Dacă această proprietate este valabilă pentru orice punct din domeniul definiției funcției, atunci funcția se spune că este continuă. În acest caz se spune că $f(x)\in C(A,\mathbb {R} )$ ${\ displaystyle f (x) \ în C (A, \ mathbb {R})}$ $f (x) \ în C (A, \ mathbb {R})$ , care este setul continuu de funcții reale și variabile în $LA$ ${\ displaystyle A}$ $LA$ .

Mai intuitiv, dacă doriți această funcție $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ disti de o mică valoare din $f(p)$ ${\ displaystyle f (p)}$ $f (p)$ trebuie doar să ne restrângem la un cartier destul de mic $p$ ${\ displaystyle p}$ $p$ . Dacă acest lucru este posibil, indiferent de distanța aleasă (cu excepția cazului în care se restrânge în continuare vecinătatea $p$ ${\ displaystyle p}$ $p$ ), atunci funcția este continuă în $p$ ${\ displaystyle p}$ $p$ .

Această definiție este echivalentă cu cea dată anterior: este construită din prima pur și simplu făcând explicită definiția limitei unei funcții. A fost folosit pentru prima dată de Cauchy . ^[2]

Funcții între spațiile topologice

f este continuu la un punct x ∈ X dacă (și numai dacă) pentru fiecare vecinătate V a lui f ( x ) există o vecinătate U a x astfel încât f ( U ) ⊆ V. Intuitiv, oricât de mic este V , există întotdeauna un U care conține x care este mapat la V.

Definiția continuității dată în cazul funcțiilor reale poate fi generalizată în contexte mai largi, precum cel al spațiilor topologice .

Să existe două spații topologice $(X,\tau _{1})$ ${\ displaystyle (X, \ tau _ {1})}$ $(X, \ tau_1)$ , $(Y,\tau _{2})$ ${\ displaystyle (Y, \ tau _ {2})}$ $(Y, \ tau_2)$ și fie $f:X\to Y$ ${\ displaystyle f: X \ to Y}$ ${\ displaystyle f: X \ to Y}$ o aplicatie. Atunci:

$f$ ${\ displaystyle f}$ $f$ se spune continuă în $x_{0}\in X$ ${\ displaystyle x_ {0} \ în X}$ $x_0 \ în X$ de sine $\forall \ V$ ${\ displaystyle \ forall \ V}$ ${\ displaystyle \ forall \ V}$ în jurul or $f(x_{0})$ ${\ displaystyle f (x_ {0})}$ $f (x_0)$ $\exists \ U$ ${\ displaystyle \ există \ U}$ ${\ displaystyle \ există \ U}$ în jurul or $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ astfel încât $f(U)\subseteq V$ ${\ displaystyle f (U) \ subseteq V}$ ${\ displaystyle f (U) \ subseteq V}$ ;

$f$ ${\ displaystyle f}$ $f$ se spune continuă dacă $\forall \ A$ ${\ displaystyle \ forall \ A}$ ${\ displaystyle \ forall \ A}$ deschide în $Da$ ${\ displaystyle Y}$ $Da$ $f^{-1}(A)=\{x\in X|f(x)\in A\}$ ${\ displaystyle f ^ {- 1} (A) = \ {x \ în X | f (x) \ în A \}}$ $f ^ {- 1} (A) = \ {x \ în X | f (x) \ în A \}$ este un set deschis în $X$ ${\ displaystyle X}$ $X$ .

Observăm că alte definiții echivalente ale funcției continue sunt:

$f$ ${\ displaystyle f}$ $f$ este continuu în fiecare punct $x\in X$ ${\ displaystyle x \ în X}$ $x \ în X$ ;
$\forall \ B\in \Gamma$ ${\ displaystyle \ forall \ B \ in \ Gamma}$ ${\ displaystyle \ forall \ B \ in \ Gamma}$ $f^{-1}(B)$ ${\ displaystyle f ^ {- 1} (B)}$ ${\ displaystyle f ^ {- 1} (B)}$ este deschis în $X$ ${\ displaystyle X}$ $X$ cu $\Gamma$ ${\ displaystyle \ Gamma}$ $\Gamă$ o bază a topologiei $\tau _{2}$ ${\ displaystyle \ tau _ {2}}$ $\ tau_2$ ;
$\forall \ P\in \Pi$ ${\ displaystyle \ forall \ P \ in \ Pi}$ ${\ displaystyle \ forall \ P \ in \ Pi}$ $f^{-1}(P)$ ${\ displaystyle f ^ {- 1} (P)}$ ${\ displaystyle f ^ {- 1} (P)}$ este deschis în $X$ ${\ displaystyle X}$ $X$ cu $\Pi$ ${\ displaystyle \ Pi}$ $\ Pi$ o pre-bază a topologiei $\tau _{2}$ ${\ displaystyle \ tau _ {2}}$ $\ tau_2$ ;
$\forall \ C$ ${\ displaystyle \ forall \ C}$ ${\ displaystyle \ forall \ C}$ închis în $Da$ ${\ displaystyle Y}$ $Da$ $f^{-1}(C)$ ${\ displaystyle f ^ {- 1} (C)}$ ${\ displaystyle f ^ {- 1} (C)}$ este închis în $X$ ${\ displaystyle X}$ $X$ ;
$\forall \ T\subseteq Y$ ${\ displaystyle \ forall \ T \ subseteq Y}$ ${\ displaystyle \ forall \ T \ subseteq Y}$ $Cl(f^{-1}(T))\subseteq f^{-1}(Cl(T))$ ${\ displaystyle Cl (f ^ {- 1} (T)) \ subseteq f ^ {- 1} (Cl (T))}$ ${\ displaystyle Cl (f ^ {- 1} (T)) \ subseteq f ^ {- 1} (Cl (T))}$ cu $C. L$ ${\ displaystyle Cl}$ ${\ displaystyle Cl}$ închiderea unui subset;
$\forall \ S\subseteq X$ ${\ displaystyle \ forall \ S \ subseteq X}$ ${\ displaystyle \ forall \ S \ subseteq X}$ $f(Cl(S))\subseteq Cl(f(S))$ ${\ displaystyle f (Cl (S)) \ subseteq Cl (f (S))}$ ${\ displaystyle f (Cl (S)) \ subseteq Cl (f (S))}$ cu $C. L$ ${\ displaystyle Cl}$ ${\ displaystyle Cl}$ închiderea unui subset.

Definiția continuității este strict legată de topologia aleasă în domeniu și în gamă: funcțiile continue cu unele opțiuni de topologie s-ar putea să nu fie așa cu altele. De exemplu, funcția de identitate este continuă dacă spațiul de sosire are aceeași topologie ca spațiul de pornire sau dacă are unul mai puțin fin , adică cu mai puține spații deschise. Dacă, pe de altă parte, spațiul de sosire are o topologie mai fină, cu altele mai deschise, funcția de identitate nu este continuă.

Funcții între spații metrice

Spațiile metrice sunt spații topologice în care topologia este generată de o bază de vecinătăți circulare. ^[3] Ambele $f$ ${\ displaystyle f}$ $f$ o funcție între două spații metrice $(X,d_{1})$ ${\ displaystyle (X, d_ {1})}$ $(X, d_1)$ Și $(Y,d_{2})$ ${\ displaystyle (Y, d_ {2})}$ $(Y, d_2)$ . Se spune că funcția f este continuă la un moment dat $p$ ${\ displaystyle p}$ $p$ dacă, pentru fiecare alegere de $\varepsilon >0$ ${\ displaystyle \ varepsilon> 0}$ $\ varepsilon> 0$ , este un $\delta >0$ ${\ displaystyle \ delta> 0}$ $\ delta> 0$ , astfel încât, pentru fiecare punct $x\in X$ ${\ displaystyle x \ în X}$ $x \ în X$ care este mai mic de $\delta$ ${\ displaystyle \ delta}$ $\ delta$ din $p$ ${\ displaystyle p}$ $p$ , sau asta:

d_{1}(x,p)<\delta

{\ displaystyle d_ {1} (x, p) <\ delta}

d_1 (x, p) <\ delta

avem asta $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este pentru mai puțin de $\varepsilon$ ${\ displaystyle \ varepsilon}$ $\ varepsilon$ din $f(p)$ ${\ displaystyle f (p)}$ $f (p)$ , adică: ^[4]

d_{2}(f(x),f(p))<\varepsilon

{\ displaystyle d_ {2} (f (x), f (p)) <\ varepsilon}

d_2 (f (x), f (p)) <\ varepsilon

Definiția poate fi scrisă folosind noțiunea de vecinătate sferică $B_{r}(P)$ ${\ displaystyle B_ {r} (P)}$ $B_r (P)$ centrat în $p$ ${\ displaystyle p}$ $p$ , de rază $\delta$ ${\ displaystyle \ delta}$ $\ delta$ : în acest caz, funcția este continuă dacă $x\in B_{\delta }(p)\cap E$ ${\ displaystyle x \ în B _ {\ delta} (p) \ cap E}$ $x \ in B_ \ delta (p) \ cap E$ presupune că $f(x)\in B_{\varepsilon }(f(p))$ ${\ displaystyle f (x) \ în B _ {\ varepsilon} (f (p))}$ $f (x) \ în B_ \ varepsilon (f (p))$ sau, simbolic:

\forall \varepsilon >0\quad \exists \delta >0:f(E\cap B_{\delta }(p))\subset B_{\varepsilon }(f(p))

{\ displaystyle \ forall \ varepsilon> 0 \ quad \ exists \ delta> 0: f (E \ cap B _ {\ delta} (p)) \ subset B _ {\ varepsilon} (f (p))}

\ forall \ varepsilon> 0 \ quad \ există \ delta> 0: f (E \ cap B_ \ delta (p)) \ subset B_ \ varepsilon (f (p))

unde este $ȘI$ ${\ displaystyle E}$ $ȘI$ este setul de definiții al $f$ ${\ displaystyle f}$ $f$ . ^[4]

În cazul funcțiilor reale, definițiile coincid dacă cele două distanțe pe domeniu și interval nu sunt altceva decât modulul diferenței dintre două valori în $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ .

Mai mult, această definiție este valabilă pentru funcțiile definite și evaluate în toate spațiile vectoriale normate , unde distanța este norma diferenței dintre două puncte. În special, este valabil în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ cu norma euclidiană și, prin urmare, extinde definiția continuității la funcțiile mai multor variabile.

Exemple

O funcție cubică, exprimată printr-un polinom de gradul trei, este o funcție continuă.

Exemple de funcții continue sunt:

Funcțiile constante $f(x)=c$ ${\ displaystyle f (x) = c}$ $f (x) = c$ .
Funcția de identitate $f(x)=x$ ${\ displaystyle f (x) = x}$ $f (x) = x$ dintr-un spațiu topologic $(X,\tau _{1})$ ${\ displaystyle (X, \ tau _ {1})}$ $(X, \ tau_1)$ în același spațiu $(X,\tau _{2})$ ${\ displaystyle (X, \ tau _ {2})}$ $(X, \ tau_2)$ , unde este $\tau _{2}$ ${\ displaystyle \ tau _ {2}}$ $\ tau_2$ este aceeași topologie ca domeniul sau o topologie mai puțin fină .
Funcții care se leagă de o pereche de numere $(x,y)$ ${\ displaystyle (x, y)}$ $(X y)$ suma $x+y$ ${\ displaystyle x + y}$ $x + y$ , produsul $X y$ ${\ displaystyle xy}$ $X y$ sau relația $x/y$ ${\ displaystyle x / y}$ $X y$ sunt continue în definiția lor setată în $\mathbb {R} ^{2}$ ${\ displaystyle \ mathbb {R} ^ {2}}$ $\ R ^ 2$ .
Transformări liniare între spațiile euclidiene
Funcții exprimate prin polinoame , cum ar fi de exemplu $f(x)=x^{3}+2x^{2}-3x+2$ ${\ displaystyle f (x) = x ^ {3} + 2x ^ {2} -3x + 2}$ $f (x) = x ^ 3 + 2x ^ 2-3x + 2$ .
Funcțiile raționale , în toate punctele în care sunt definite, sau în toate punctele în care numitorul nu este anulat.
Funcția exponențială și logaritmul natural în seturile lor definitorii , adică $f(x)=\exp(x)$ ${\ displaystyle f (x) = \ exp (x)}$ $f (x) = \ exp (x)$ Și $f(x)=\log(x)$ ${\ displaystyle f (x) = \ log (x)}$ $f (x) = \ log (x)$ .
Funcțiile sinus și cosinus , adică $f(x)=\cos(x)$ ${\ displaystyle f (x) = \ cos (x)}$ $f (x) = \ cos (x)$ Și $f(x)=\sin(x)$ ${\ displaystyle f (x) = \ sin (x)}$ $f (x) = \ sin (x)$ .
Funcția de valoare absolută $f(x)=|x|$ ${\ displaystyle f (x) = | x |}$ $f (x) = | x |$ este continuu (dar nu derivabil în $x=0$ ${\ displaystyle x = 0}$ $x = 0$ ).
Funcția Cantor și curba Koch sunt exemple de funcții continue cu structură fractală .
Curba Peano : o curbă plană care acoperă întregul pătrat.

Funcția Heaviside are o discontinuitate în 0.

Exemple de funcții non- continue sunt:

Funcția Heaviside , definită ca

H(x)={\begin{cases}1&{\text{se }}x\geq 0\\0&{\text{se }}x<0.\end{cases}}

{\ displaystyle H (x) = {\ begin {cases} 1 & {\ text {se}} x \ geq 0 \\ 0 & {\ text {se}} x <0. \ end {cases}}}

H (x) = \ begin {cases} 1 & \ text {se} x \ ge 0 \\ 0 & \ text {se} x <0. \ End {cases}

Funcția indicator a unui subset corespunzător de $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ R$ este discontinuu la frontiera întregului.
Funcția Dirichlet este discontinuă în orice moment.

Proprietățile funcțiilor continue

Este $f:I\to \mathbb {R}$ ${\ displaystyle f: I \ to \ mathbb {R}}$ $f: I \ to \ R$ o funcție continuă cu valoare reală definită pe un interval $THE$ ${\ displaystyle I}$ $THE$ . Merită:

Permanența semnului : Dacă într-un punct $p$ ${\ displaystyle p}$ $p$ a domeniului său $f(p)>0$ ${\ displaystyle f (p)> 0}$ $f (p)> 0$ , apoi există un cartier $U(p)$ ${\ displaystyle U (p)}$ $Sus)$ astfel încât $f(x)>0$ ${\ displaystyle f (x)> 0}$ $f (x)> 0$ în toate punctele din jur.
Teorema valorii intermediare : dacă $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ sunt două puncte de stăpânire, atunci $f$ ${\ displaystyle f}$ $f$ își asumă toate valorile între $f(a)$ ${\ displaystyle f (a)}$ $face)$ Și $f(b)$ ${\ displaystyle f (b)}$ $f (b)$ .
Teorema Bolzano : dacă $la$ ${\ displaystyle a}$ $la$ Și $b$ ${\ displaystyle b}$ $b$ sunt două puncte ale domeniului astfel încât $f(a)\cdot f(b)\,<\,0$ ${\ displaystyle f (a) \ cdot f (b) \, <\, 0}$ $f (a) \ cdot f (b) \, <\, 0$ (adică dacă $f(a)$ ${\ displaystyle f (a)}$ $face)$ Și $f(b)$ ${\ displaystyle f (b)}$ $f (b)$ au un semn diferit), atunci există cel puțin unul $p\in (a,b)$ ${\ displaystyle p \ in (a, b)}$ $p \ in (a, b)$ astfel încât $f(p)=0.$ ${\ displaystyle f (p) = 0.}$ $f (p) = 0.$
Teorema Weierstrass : dacă intervalul $THE$ ${\ displaystyle I}$ $THE$ este închis și limitat, adică dacă $I=[a,b]$ ${\ displaystyle I = [a, b]}$ $I = [a, b]$ , asa de $f$ ${\ displaystyle f}$ $f$ admite maxim și minim, adică există două puncte $p$ ${\ displaystyle p}$ $p$ Și $q$ ${\ displaystyle q}$ $q$ astfel încât $f(p)\leq f(x)\leq f(q)$ ${\ displaystyle f (p) \ leq f (x) \ leq f (q)}$ $f (p) \ leq f (x) \ leq f (q)$ pentru fiecare $x\in [a,b]$ ${\ displaystyle x \ in [a, b]}$ $x \ în [a, b]$ .

De sine $f$ ${\ displaystyle f}$ $f$ este o funcție continuă bijectivă cu valoare reală definită pe un interval, atunci $f$ ${\ displaystyle f}$ $f$ este strict monotonă și funcția inversă $f^{-1}$ ${\ displaystyle f ^ {- 1}}$ $f ^ {- 1}$ este continuu și strict monoton. Implicația nu se aplică în general funcțiilor al căror domeniu nu este un interval . ^[5]

Este $f:(X,d_{1})\to (Y,d_{2})$ ${\ displaystyle f: (X, d_ {1}) \ to (Y, d_ {2})}$ $f: (X, d_1) \ to (Y, d_2)$ o funcție între spațiile metrice. Merită:

Teorema Weierstrass : dacă $X$ ${\ displaystyle X}$ $X$ atunci este un întreg compact $f$ ${\ displaystyle f}$ $f$ presupune maxim și minim în $X$ ${\ displaystyle X}$ $X$ . În special, ele există $p,q\in X$ ${\ displaystyle p, q \ în X}$ $p, q \ în X$ astfel încât $f(p)\leq f(x)\leq f(q)$ ${\ displaystyle f (p) \ leq f (x) \ leq f (q)}$ $f (p) \ leq f (x) \ leq f (q)$ pentru fiecare $x\in X$ ${\ displaystyle x \ în X}$ $x \ în X$ .
De sine $f$ ${\ displaystyle f}$ $f$ este bidirecțional e $X$ ${\ displaystyle X}$ $X$ atunci este compact $f^{-1}$ ${\ displaystyle f ^ {- 1}}$ $f ^ {- 1}$ și continuă.
Heine - Teorema Cantor : dacă $X$ ${\ displaystyle X}$ $X$ atunci este compact $f$ ${\ displaystyle f}$ $f$ este uniform continuu .
De sine $f(x)=(f_{1}(x),\dots ,f_{n}(x))$ ${\ displaystyle f (x) = (f_ {1} (x), \ dots, f_ {n} (x))}$ $f (x) = (f_1 (x), \ dots, f_n (x))$ , asa de $f$ ${\ displaystyle f}$ $f$ este continuu dacă și numai dacă fiecare funcție este continuă $f_{i}(x)$ ${\ displaystyle f_ {i} (x)}$ $f_i (x)$ . Prin urmare, acest rezultat este valabil pentru funcții $f(x):\mathbb {R} \to \mathbb {R} ^{n}$ ${\ displaystyle f (x): \ mathbb {R} \ to \ mathbb {R} ^ {n}}$ ${\ displaystyle f (x): \ mathbb {R} \ to \ mathbb {R} ^ {n}}$ . ^[5]

Este $f:(X,\tau _{1})\to (Y,\tau _{2})$ ${\ displaystyle f: (X, \ tau _ {1}) \ to (Y, \ tau _ {2})}$ $f: (X, \ tau_1) \ to (Y, \ tau_2)$ o funcție continuă între spațiile topologice. Merită:

Imaginea contra unui set deschis este un set deschis. În general, nu este adevărat că imaginea unui set deschis este un set deschis.
Imaginea contra unui set închis este un set închis.
Imaginea unui set compact este un set compact.
Un set de conectat imagine este un set conectat. ^[5]
Imaginea unui set conectat de margini este un set conectat de margini.

Compoziţie

Compoziția funcțiilor continue este o funcție continuă, adică dacă $f$ ${\ displaystyle f}$ $f$ Și $g$ ${\ displaystyle g}$ $g$ sunt două funcții continue, apoi și:

h(x)=(f\circ g)(x)=f(g(x))

{\ displaystyle h (x) = (f \ circ g) (x) = f (g (x))}

h (x) = (f \ circ g) (x) = f (g (x))

este o funcție continuă.

Ca o consecință a acestei proprietăți avem următoarele:

Suma $f+g$ ${\ displaystyle f + g}$ $f + g$ a două funcții continue este o funcție continuă.
Produsul $f\cdot g$ ${\ displaystyle f \ cdot g}$ $f \ cdot g$ a două funcții continue este o funcție continuă.
Coeficientul $f/g$ ${\ displaystyle f / g}$ $f / g$ a două funcții continue este o funcție continuă (în setul definitoriu, adică unde $g$ ${\ displaystyle g}$ $g$ este diferit de 0).

În general, inversul nu este adevărat: de exemplu, dacă o funcție continuă este suma a două funcții, nu este sigur că ambele adunări sunt ele însele funcții continue. ^[5] De exemplu dacă

f(x)={\begin{cases}0\quad {\text{se }}x\neq 1\\1\quad {\text{se }}x=1\end{cases}}\quad {\text{e}}\quad g(x)={\begin{cases}1\quad {\text{se }}x\neq 1\\0\quad {\text{se }}x=1\end{cases}},

{\ displaystyle f (x) = {\ begin {cases} 0 \ quad {\ text {se}} x \ neq 1 \\ 1 \ quad {\ text {se}} x = 1 \ end {cases}} \ quad {\ text {e}} \ quad g (x) = {\ begin {cases} 1 \ quad {\ text {se}} x \ neq 1 \\ 0 \ quad {\ text {se}} x = 1 \ end {cases}},}

f (x) = \ begin {cases} 0 \ quad \ text {se} x \ neq 1 \\ 1 \ quad \ text {se} x = 1 \ end {cases} \ quad \ text {e} \ quad g (x) = \ begin {cases} 1 \ quad \ text {se} x \ neq 1 \\ 0 \ quad \ text {se} x = 1 \ end {cases},

asa de $f$ ${\ displaystyle f}$ $f$ Și $g$ ${\ displaystyle g}$ $g$ nu sunt continue, dar

f(x)+g(x)=1\quad {\text{e}}\quad f(x)g(x)=0

{\ displaystyle f (x) + g (x) = 1 \ quad {\ text {e}} \ quad f (x) g (x) = 0}

f (x) + g (x) = 1 \ quad \ text {e} \ quad f (x) g (x) = 0

amândoi sunt continuați în toate $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ . În mod similar, dacă

f(x)={\begin{cases}3\quad {\text{se }}x\neq 1\\9\quad {\text{se }}x=1\end{cases}}\quad {\text{e}}\quad g(x)={\begin{cases}1\quad {\text{se }}x\neq 1\\3\quad {\text{se }}x=1\end{cases}},

{\ displaystyle f (x) = {\ begin {cases} 3 \ quad {\ text {se}} x \ neq 1 \\ 9 \ quad {\ text {se}} x = 1 \ end {cases}} \ quad {\ text {e}} \ quad g (x) = {\ begin {cases} 1 \ quad {\ text {se}} x \ neq 1 \\ 3 \ quad {\ text {se}} x = 1 \ end {cases}},}

f (x) = \ begin {cases} 3 \ quad \ text {se} x \ neq 1 \\ 9 \ quad \ text {se} x = 1 \ end {cases} \ quad \ text {e} \ quad g (x) = \ begin {cases} 1 \ quad \ text {se} x \ neq 1 \\ 3 \ quad \ text {se} x = 1 \ end {cases},

asa de $f$ ${\ displaystyle f}$ $f$ Și $g$ ${\ displaystyle g}$ $g$ nu sunt continue, dar

{\frac {f(x)}{g(x)}}=3

{\ displaystyle {\ frac {f (x)} {g (x)}} = 3}

\ frac {f (x)} {g (x)} = 3

este continuu pe toate $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ .

Succesiuni

Animația arată o secvență de funcții continue care indică o funcție discontinuă

Având în vedere o succesiune de funcții continue $f_{1},f_{2},\dotsc \colon I\to \mathbb {R}$ ${\ displaystyle f_ {1}, f_ {2}, \ dotsc \ colon I \ to \ mathbb {R}}$ $f_1, f_2, \ dotsc \ colon I \ to \ R$ astfel încât limita:

f(x):=\lim _{n\to \infty }f_{n}(x)

{\ displaystyle f (x): = \ lim _ {n \ to \ infty} f_ {n} (x)}

f (x): = \ lim_ {n \ to \ infty} f_n (x)

există finit pentru fiecare $x\in \mathbb {R}$ ${\ displaystyle x \ in \ mathbb {R}}$ $x \ in \ mathbb {R}$ (convergență punctuală), atunci nu este neapărat adevărat că $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este o funcție continuă. Cu toate acestea, dacă secvența converge uniform , atunci punctul limită $f(x)$ ${\ displaystyle f (x)}$ $f (x)$ este continuu. ^[6]

Derivarea și integrarea

O funcție diferențiată (sau mai general o funcție diferențiată ) la un moment dat $p$ ${\ displaystyle p}$ $p$ este întotdeauna continuu în acel moment. Reversul nu este adevărat: există funcții continue nedirectabile, cum ar fi funcția de valoare absolută , care este continuă, dar nu derivabilă în același punct. Există, de asemenea, funcții variabile reale care sunt continue în toate punctele domeniului și nu se pot diferenția în niciunul dintre ele, cum ar fi funcția Weierstrass .

O funcție continuă $f:[a,b]\rightarrow \mathbb {R}$ ${\ displaystyle f: [a, b] \ rightarrow \ mathbb {R}}$ $f: [a, b] \ rightarrow \ mathbb {R}$ este întotdeauna integrabilă după Riemann (și deci și după Lebesgue ). În plus, $f$ ${\ displaystyle f}$ $f$ admite întotdeauna primitive și fiecare dintre primitive este continuă. În schimb, nu toate funcțiile integrabile sunt continue: de exemplu, toate funcțiile constante în bucăți sunt integrabile. ^[7]

Alte tipuri de continuitate

Continuitate prin succesiuni

O functie $f$ ${\ displaystyle f}$ $f$ la valori reale este continuu pentru secvențe în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ dacă, pentru fiecare succesiune $x_{n}$ ${\ displaystyle x_ {n}}$ $x_ {n}$ la valorile din domeniul funcției și convergente la $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ , succesiunea $f(x_{n})$ ${\ displaystyle f (x_ {n})}$ ${\ displaystyle f (x_ {n})}$ converge la $f(x_{0})$ ${\ displaystyle f (x_ {0})}$ $f (x_0)$ .

Această formulare a continuității se datorează lui Eduard Heine .

O funcție continuă este întotdeauna continuă pentru secvențe, în timp ce, dimpotrivă, este posibil să se dea exemple de funcții continue pentru secvențe, dar nu continuă. Reversul este adevărat numai dacă domeniul $\scriptstyle {X}$ ${\ displaystyle \ scriptstyle {X}}$ $\ scriptstyle {X}$ este un spațiu secvențial , la fel ca spațiile prime-numărabile ^[8] și, prin urmare, în special spațiile metrice : în acest caz, prin urmare, cele două definiții pot fi considerate echivalente. ^[9]

Continuitate stânga și dreapta

O funcție continuă spre dreapta

O funcție reală $f$ ${\ displaystyle f}$ $f$ se spune continuă chiar în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ de sine:

\lim _{x\to x_{0}^{+}}f(x)=f(x_{0})

{\ displaystyle \ lim _ {x \ to x_ {0} ^ {+}} f (x) = f (x_ {0})}

\ lim_ {x \ to x_0 ^ +} f (x) = f (x_0)

unde limita este destinată doar drept limită potrivită .

O functie $f$ ${\ displaystyle f}$ $f$ se spune continuă stânga în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ de sine:

\lim _{x\to x_{0}^{-}}f(x)=f(x_{0})

{\ displaystyle \ lim _ {x \ to x_ {0} ^ {-}} f (x) = f (x_ {0})}

\ lim_ {x \ to x_0 ^ -} f (x) = f (x_0)

O funcție este continuă într-un punct dacă și numai dacă este continuă la stânga și la dreapta acolo.

Aceste proprietăți nu pot fi extinse la funcții cu mai multe variabile, ca în plan, în spațiu și, în general, în $\mathbb {R} ^{n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ cand $n>1$ ${\ displaystyle n> 1}$ $n> 1$ nu există o relație de ordine , adică nu este posibil să se definească o „dreapta” sau o „stânga”.

Semi-continuitate

O funcție semicontinuă de mai jos: la punctul de salt,

f(x_{0})

{\ displaystyle f (x_ {0})}

f (x_0)

este situat în partea de jos

Același subiect în detaliu: Funcția semi-continuă .

O functie $f$ ${\ displaystyle f}$ $f$ definit pe un spațiu topologic $X$ ${\ displaystyle X}$ $X$ la valorile reale se spune semicontinuu inferior în $x_{0}\in X$ ${\ displaystyle x_ {0} \ în X}$ $x_0 \ în X$ dacă pentru fiecare $\varepsilon >0$ ${\ displaystyle \ varepsilon> 0}$ $\ varepsilon> 0$ există un cartier $U$ ${\ displaystyle U}$ $U$ din $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ astfel încât pentru fiecare $x\in U$ ${\ displaystyle x \ în U}$ $x \ în U$ , avem:

f(x)>f(x_{0})-\varepsilon

{\ displaystyle f (x)> f (x_ {0}) - \ varepsilon}

{\ displaystyle f (x)> f (x_ {0}) - \ varepsilon}

Dacă, pe de altă parte, este adevărat, pentru fiecare $x\in U$ ${\ displaystyle x \ în U}$ $x \ în U$ :

f(x)<f(x_{0})+\varepsilon

{\ displaystyle f (x) <f (x_ {0}) + \ varepsilon}

{\ displaystyle f (x) <f (x_ {0}) + \ varepsilon}

funcția se numește semicontinuă în partea de sus în $x_{0}$ ${\ displaystyle x_ {0}}$ $x_0$ .

Dacă prima (sau respectiv a doua) proprietate deține în fiecare punct al domeniului, funcția se spune că este semicontinuă dedesubt (sau respectiv semicontinuă deasupra).

Semicontinuitatea (atât inferioară, cât și superioară), este o proprietate mai slabă a continuității: există funcții semi-continue, dar nu continue. În schimb, o funcție este continuă dacă și numai dacă este atât semicontinuă dedesubt, cât și semicontinuă deasupra.

Continuitate separată

Același subiect în detaliu: Continuitate separată .

În cazul funcțiilor mai multor variabile, este posibil să se definească o condiție mai slabă de continuitate, numită continuitate separată : o funcție $f$ ${\ displaystyle f}$ $f$ este continuu separat la un moment dat $p$ ${\ displaystyle p}$ $p$ în ceea ce privește una dintre variabile $x_{i}$ ${\ displaystyle x_ {i}}$ $x_i$ dacă funcția unei variabile dependente doar de parametru este continuă $x_{i}$ ${\ displaystyle x_ {i}}$ $x_i$ , lăsând variabilele rămase fixate la valoarea asumată la punctul în cauză.

Continuitate uniformă

Același subiect în detaliu: Continuitate uniformă .

O condiție de continuitate mai puternică (și mai globală) este cea a continuității uniforme : se spune că o funcție continuă între două spații metrice este uniformă continuă dacă parametrul $\delta$ ${\ displaystyle \ delta}$ $\ delta$ a definiției nu depinde de punct $p$ ${\ displaystyle p}$ $p$ considerat, adică dacă este posibil să alegeți un $\delta$ ${\ displaystyle \ delta}$ $\ delta$ care satisface definiția pentru toate punctele domeniului.

Mai exact, o funcție $f$ ${\ displaystyle f}$ $f$ este uniform continuu dacă, pentru fiecare $\varepsilon >0$ ${\ displaystyle \ varepsilon> 0}$ $\ varepsilon> 0$ este un $\delta >0$ ${\ displaystyle \ delta> 0}$ $\ delta> 0$ astfel încât, totuși, am luat două puncte $p$ ${\ displaystyle p}$ $p$ Și $q$ ${\ displaystyle q}$ $q$ în domeniul $f$ ${\ displaystyle f}$ $f$ care sunt pentru mai puțin de $\delta$ ${\ displaystyle \ delta}$ $\ delta$ , apoi imaginile lor $f(p)$ ${\ displaystyle f (p)}$ $f (p)$ Și $f(q)$ ${\ displaystyle f (q)}$ $f (q)$ sunt plecați mai puțin de $\varepsilon$ ${\ displaystyle \ varepsilon}$ $\ varepsilon$ . ^[5]

Echicontinuitate

Același subiect în detaliu: echicontinuitate .

Când elementele unui set de funcții continue au același modul de continuitate , vorbim despre un set echicontinuu . Mai exact, Siano $X$ ${\ displaystyle X}$ $X$ Și $Da$ ${\ displaystyle Y}$ $Da$ două spații metrice și $F.$ ${\ displaystyle F}$ $F.$ o familie de funcții definită de $X$ ${\ displaystyle X}$ $X$ în $Da$ ${\ displaystyle Y}$ $Da$ . Familia $F.$ ${\ displaystyle F}$ $F.$ este echicontinuu la punctul respectiv $x_{0}\in X$ ${\ displaystyle x_ {0} \ în X}$ $x_0 \ în X$ dacă pentru fiecare $\epsilon >0$ ${\ displaystyle \ epsilon> 0}$ $\ epsilon> 0$ există $\delta >0$ ${\ displaystyle \ delta> 0}$ $\ delta> 0$ astfel încât $d(f(x_{0}),f(x))<\epsilon$ ${\ displaystyle d (f (x_ {0}), f (x)) <\ epsilon}$ $d (f (x_0), f (x)) <\ epsilon$ pentru toți $f\in F$ ${\ displaystyle f \ în F}$ $f \ în F$ și pentru fiecare $X$ ${\ displaystyle x}$ $X$ astfel încât $d(x_{0},x)<\delta$ ${\ displaystyle d (x_ {0}, x) <\ delta}$ $d (x_0, x) <\ delta$ . Familia $F.$ ${\ displaystyle F}$ $F.$ este echicontinuu (în total $X$ ${\ displaystyle X}$ $X$ ) dacă este echicontinuă în fiecare dintre punctele sale. Familia $F.$ ${\ displaystyle F}$ $F.$ este uniform echicontinuu dacă pentru fiecare $\epsilon >0$ ${\ displaystyle \ epsilon> 0}$ $\ epsilon> 0$ există $\delta >0$ ${\ displaystyle \ delta> 0}$ $\ delta> 0$ astfel încât $d(f(x_{1}),f(x_{2}))<\epsilon$ ${\ displaystyle d (f (x_ {1}), f (x_ {2})) <\ epsilon}$ $d (f (x_1), f (x_2)) <\ epsilon$ pentru toți $f\in F$ ${\ displaystyle f \ în F}$ $f \ în F$ și pentru fiecare pereche de puncte $x_{1}$ ${\ displaystyle x_ {1}}$ $x_1$ Și $x_{2}$ ${\ displaystyle x_ {2}}$ $x_2$ în $X$ ${\ displaystyle X}$ $X$ astfel încât $d(x_{1},x_{2})<\delta$ ${\ displaystyle d (x_ {1}, x_ {2}) <\ delta}$ $d (x_1, x_2) <\ delta$ .

Mai general, când $X$ ${\ displaystyle X}$ $X$ este un spațiu topologic , un întreg $F.$ ${\ displaystyle F}$ $F.$ de funcții din $X$ ${\ displaystyle X}$ $X$ în $Da$ ${\ displaystyle Y}$ $Da$ este echicontinuu la punctul respectiv $x\in X$ ${\ displaystyle x \ în X}$ $x \ în X$ dacă pentru fiecare $\epsilon >0$ ${\ displaystyle \ epsilon> 0}$ $\ epsilon> 0$ ideea $X$ ${\ displaystyle x}$ $X$ deține un cartier $U_{x}$ ${\ displaystyle U_ {x}}$ $U_x$ astfel încât:

d_{Y}(f(y),f(x))<\epsilon \qquad \forall y\in U_{x}\quad \forall f\in F

{\ displaystyle d_ {Y} (f (y), f (x)) <\ epsilon \ qquad \ forall y \ in U_ {x} \ quad \ forall f \ in F}

d_Y (f (y), f (x)) <\ epsilon \ qquad \ forall y \ in U_x \ quad \ forall f \ in F

Se știe că această definiție este utilizată în contextul spațiilor vectoriale topologice .

Spațiul funcțiilor continue

Setul tuturor funcțiilor continue pe un domeniu fix $LA$ ${\ displaystyle A}$ $LA$ și valori reale:

C(A,\mathbb {R} ):=\{f:A\to \mathbb {R} {\text{ }}|{\text{ }}f{\text{ è continua}}\}

{\ displaystyle C (A, \ mathbb {R}): = \ {f: A \ to \ mathbb {R} {\ text {}} | {\ text {}} f {\ text {este continuu}} \ }}

C (A, \ R): = \ {f: A \ to \ R \ text {} | \ text {} f \ text {este continuu} \}

poate fi prevăzut cu o structură spațială vectorială prin setarea pentru $f$ ${\ displaystyle f}$ $f$ Și $g$ ${\ displaystyle g}$ $g$ într-un astfel de set:

{\begin{matrix}f+g:&A&\longrightarrow &\mathbb {R} \\&x&\longmapsto &f(x)+g(x)\end{matrix}}

{\ displaystyle {\ begin {matrix} f + g: & A & \ longrightarrow & \ mathbb {R} \\ & x & \ longmapsto & f (x) + g (x) \ end {matrix}}}

\ begin {matrix} f + g: & A & \ longrightarrow & \ R \\ & x & \ longmapsto & f (x) + g (x) \ end {matrix}

si pentru $\alpha$ ${\ displaystyle \ alpha}$ $\ alfa$ numar real:

{\begin{matrix}\alpha f:&A&\longrightarrow &\mathbb {R} \\&x&\longmapsto &\alpha f(x)\end{matrix}}

{\ displaystyle {\ begin {matrix} \ alpha f: & A & \ longrightarrow & \ mathbb {R} \\ & x & \ longmapsto & \ alpha f (x) \ end {matrix}}}

\ begin {matrix} \ alpha f: & A & \ longrightarrow & \ R \\ & x & \ longmapsto & \ alpha f (x) \ end {matrix}

Vectorul spațiul astfel definit se numește spațiul funcțiilor continue pe $LA$ ${\ displaystyle A}$ $LA$ .

Dacă domeniul $LA$ ${\ displaystyle A}$ $LA$ este compact (și, prin urmare, pentru toate funcțiile din $C(A,\mathbb {R} )$ ${\ displaystyle C (A, \ mathbb {R})}$ $MAȘINĂ)$ Teorema lui Weierstrass se menține) în spațiu $C(A,\mathbb {R} )$ ${\ displaystyle C (A, \ mathbb {R})}$ $MAȘINĂ)$ o normă poate fi definită prin setarea:

\left\|f\right\|_{\infty }:=\sup _{x\in A}f(x)

\left\|f\right\|_{\infty }:=\sup _{x\in A}f(x)

\left \| f \right \|_\infty:=\sup_{x \in A} f(x)

detta norma uniforme o norma del sup .

La coppia costituita dallo spazio $C(A,\mathbb {R} )$ $C(A,\mathbb {R} )$ $C(A,\R)$ e dalla norma uniforme individua uno spazio di Banach .

Note

^ ^a ^b Apostol, TM , pp. 130-131 .
^ Judith V. Grabiner, Who Gave You the Epsilon? Cauchy and the Origins of Rigorous Calculus ( PDF ) ^{[ collegamento interrotto ]} , in The American Mathematical Monthly , vol. 90, n. 3, marzo 1983, pp. 185–194, DOI : 10.2307/2975545 , JSTOR 2975545 .
^ Manetti, Marco , p. 50 .
^ ^a ^b Soardi, PM , pp. 175-177 .
^ ^a ^b ^c ^d ^e Soardi, PM , cap. 7 .
^ Giusti E. , cap. 13 .
^ Soardi PM , p.204 e pp. 295-301 .
^ "primo-numerabile" è la traduzione letterale del termine first-countable usato in lingua inglese. Nella letteratura matematica recente lo si preferisce a termine base locale numerabile per evitare possibili confusioni con il secondo assioma di numerabilità. Si ricorda che uno spazio topologico soddisfa il primo assioma di numerabilità se ogni suo punto ammette un sistema fondamentale di intorni numerabile.
^ Arkhangel'skii, AV , pp. 31-33 .

Bibliografia

( EN ) Michael Reed, Barry Simon, Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis , 2ª ed., San Diego, California, Academic press inc., 1980, ISBN 0-12-585050-6 .
Paolo Marcellini , Carlo Sbordone , Analisi Matematica Uno , Liguori Editore, 1998, ISBN 9788820728199 .
Paolo Maurizio Soardi, Analisi Matematica , CittàStudi, 2007, ISBN 978-88-251-7319-2 .
Marco Manetti, Topologia , Springer, 2008, ISBN 978-88-470-0756-7 .
( EN ) Tom M. Apostol, Calculus , vol. 1, John Wiley & Sons, inc., 1967, ISBN 0-471-00005-1 .
( EN ) AV Arkhangel'skii, Pontryagin, LS, General Topology I , Springer-Verlag, 1990, ISBN 3-540-18178-4 .
Nicola Fusco , Paolo Marcellini , Carlo Sbordone : Lezioni di Analisi Matematica Due , Zanichelli, 2020, ISBN 9788808520203 .
Enrico Giusti , Analisi matematica 2 , Bollati Boringhieri, 2008, ISBN 978-88-339-5706-7 .

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su funzione continua

Collegamenti esterni

( EN )Funzione continua , su Enciclopedia Britannica , Encyclopædia Britannica, Inc.
( EN ) Eric W. Weisstein,Funzione continua , in MathWorld , Wolfram Research.

Controllo di autorità	Thesaurus BNCF 53874 · LCCN ( EN ) sh85052334 · BNF ( FR ) cb12123565q (data)

Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica

[apos-1] Apostol, TM , pp. 130-131 .

[grabiner-2] Judith V. Grabiner, Who Gave You the Epsilon? Cauchy and the Origins of Rigorous Calculus ( PDF ) ^{[ collegamento interrotto ]} , in The American Mathematical Monthly , vol. 90, n. 3, marzo 1983, pp. 185–194, DOI : 10.2307/2975545 , JSTOR 2975545 .

[3] Manetti, Marco , p. 50 .

[defM-4] Soardi, PM , pp. 175-177 .

[soardi-5] Soardi, PM , cap. 7 .

[6] Giusti E. , cap. 13 .

[7] Soardi PM , p.204 e pp. 295-301 .

[8] "primo-numerabile" è la traduzione letterale del termine first-countable usato in lingua inglese. Nella letteratura matematica recente lo si preferisce a termine base locale numerabile per evitare possibili confusioni con il secondo assioma di numerabilità. Si ricorda che uno spazio topologico soddisfa il primo assioma di numerabilità se ogni suo punto ammette un sistema fondamentale di intorni numerabile.

[9] Arkhangel'skii, AV , pp. 31-33 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

V · D · M Analisi matematica
Calcolo infinitesimale	Numero reale · Infinitesimo · O-grande · Successione ( di funzioni ) · Successione di Cauchy · Teorema di Bolzano-Weierstrass · Stima asintotica · Limite ( di una funzione · di una successione · Forma indeterminata ) · Teorema dei due carabinieri · Limite notevole · Punto di accumulazione · Punto isolato · Intorno · Serie ( di funzioni ) · Criteri di convergenza ·Limite di funzioni a più variabili
Studio della continuità	Funzione continua · Punto di discontinuità · Continuità uniforme · Funzione lipschitziana · Teorema di Bolzano · Teorema di Weierstrass · Teorema dei valori intermedi · Teorema di Heine-Cantor · Modulo di continuità · Funzione semicontinua · Continuità separata · Teorema di approssimazione di Weierstrass
Calcolo differenziale	Derivata · Differenziale · Regole di derivazione · Teorema di Fermat · Teorema di Rolle · Teorema di Lagrange · Teorema di Cauchy · Teorema di Darboux · Teorema di Taylor · Serie di Taylor · Funzione differenziabile · Gradiente · Jacobiana · Hessiana · Forma differenziale · Generalizzazioni della derivata · Derivata parziale · Derivata mista
Integrale	Primitiva · Integrale di Riemann · Integrale improprio · Integrale di Lebesgue · Teorema fondamentale · Metodi di integrazione · Tavole · Integrale multiplo , di linea ( 1ª specie · 2ª specie ) e di superficie ( di volume )
Studio di funzione	Funzione · Variabile · Dominio e codominio · Funzioni pari e dispari · Funzione periodica · Funzione monotona · Funzione convessa · Massimo e minimo di una funzione · Punto angoloso · Cuspide · Punto di flesso · Asintoto · Grafico di una funzione · Funzione iniettiva
Disuguaglianze	Disuguaglianza triangolare · Disuguaglianza di Cauchy-Schwarz · Bernoulli · Jensen · Hölder · Young · Minkowski
Altro	Approssimazione di Stirling · Prodotto di Wallis · Funzione Gamma · Teorema delle funzioni implicite · Teorema della funzione inversa · Funzione hölderiana · Spazio metrico · Spazio normato · Intervallo · Insieme trascurabile · Insieme chiuso · Insieme aperto · Palla · Omeomorfismo · Omeomorfismo locale · Diffeomorfismo · Diffeomorfismo locale · Classe C di una funzione · Equazione differenziale · Problema di Cauchy